【问题描述】[中等]

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的连续子数组，返回 0。示例: 输入: s = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。

【解答思路】

1. 暴力法

• 初始化子数组的最小长度为无穷大
• 枚举数组nums 中的每个下标作为子数组的开始下标，对于每个开始下标 i，需要找到大于或等于 i 的最小下标 j，使得从 nums[i] 到nums[j] 的元素和大于或等于 s，并更新子数组的最小长度（此时子数组的长度是 j-i+1）。

时间复杂度：O(N^2) 空间复杂度：O(1)

class Solution {public int minSubArrayLen(int s, int[] nums) {int n = nums.length;if (n == 0) {return 0;}int ans = Integer.MAX_VALUE;for (int i = 0; i < n; i++) {int sum = 0;for (int j = i; j < n; j++) {sum += nums[j];if (sum >= s) {ans = Math.min(ans, j - i + 1);break;}}}return ans == Integer.MAX_VALUE ? 0 : ans;}
}

2. 前缀和

时间复杂度：O(N^2) 空间复杂度：O(N)

public int minSubArrayLen(int s, int[] nums) {int n = nums.length;if (n == 0) {return 0;}int[] sums = new int[n];sums[0] = nums[0];for (int i = 1; i < n; i++) {sums[i] = nums[i] + sums[i - 1];}int min = Integer.MAX_VALUE;for (int i = 0; i < n; i++) {int s2 = s - nums[i]; //除去当前数字for (int j = i; j < n; j++) {//i + 1 到  j 的所有数字和if (sums[j] - sums[i] >= s2) {min = Math.min(min, j - i + 1);}}}return min == Integer.MAX_VALUE ? 0 : min;
}

3. 前缀和+二分

时间复杂度：O(NlogN) 空间复杂度：O(N)

class Solution {public int minSubArrayLen(int s, int[] nums) {int n = nums.length;if (n == 0) {return 0;}int ans = Integer.MAX_VALUE;int[] sums = new int[n + 1]; // 为了方便计算，令 size = n + 1 // sums[0] = 0 意味着前 0 个元素的前缀和为 0// sums[1] = A[0] 前 1 个元素的前缀和为 A[0]// 以此类推for (int i = 1; i <= n; i++) {sums[i] = sums[i - 1] + nums[i - 1];}for (int i = 1; i <= n; i++) {int target = s + sums[i - 1];int bound = Arrays.binarySearch(sums, target);if (bound < 0) {bound = -bound - 1;}if (bound <= n) {ans = Math.min(ans, bound - (i - 1));}}return ans == Integer.MAX_VALUE ? 0 : ans;}
}

另一写法

public int minSubArrayLen(int s, int[] nums) {int n = nums.length;if (n == 0) {return 0;}int[] sums = new int[n];sums[0] = nums[0];for (int i = 1; i < n; i++) {sums[i] = nums[i] + sums[i - 1];}int min = Integer.MAX_VALUE;for (int i = 0; i < n; i++) {int s2 = s - nums[i];//二分查找，目标值是 s2 + sums[i]int k = binarySearch(i, n - 1, sums, s2 + sums[i]);if (k != -1) {min = Math.min(min, k - i + 1);}}return min == Integer.MAX_VALUE ? 0 : min;
}//寻求刚好大于 target 的 sums 的下标，也就是大于等于 target 所有 sums 中最小的那个
private int binarySearch(int start, int end, int[] sums, int target) {int mid = -1;while (start <= end) {mid = (start + end) >>> 1;if (sums[mid] == target) {return mid;} else if (sums[mid] < target) {start = mid + 1;} else {end = mid - 1;}}//是否找到，没有找到返回 -1return sums[mid] > target ? mid : -1;
}/*
private int binarySearch(int start, int end, int[] sums, int target) {int mid = -1;while (start < end) {mid = (start + end) >>> 1;if (sums[mid] < target) {start = mid + 1;} else {end = mid ;}}//是否找到，没有找到返回 -1return sums[start] >= target ?start : -1;
}*/

4. 双指针

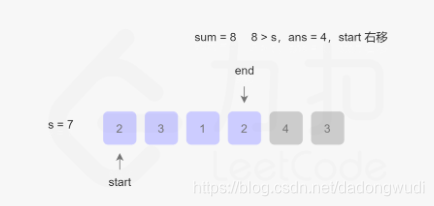
时间复杂度：O(N) 空间复杂度：O(1)

class Solution {public int minSubArrayLen(int s, int[] nums) {int n = nums.length;if (n == 0) {return 0;}int ans = Integer.MAX_VALUE;int start = 0, end = 0;int sum = 0;while (end < n) {sum += nums[end];while (sum >= s) {ans = Math.min(ans, end - start + 1);sum -= nums[start];start++;}end++;}return ans == Integer.MAX_VALUE ? 0 : ans;}
}

【总结】

1.涉及连续子数组的问题，我们通常有两种思路：一是滑动窗口、二是前缀和

2.二分查找的关键就是那个递增的有序数列，从而可以每次抛弃一半的可选解。

3.Arrays类的binarySearch()方法

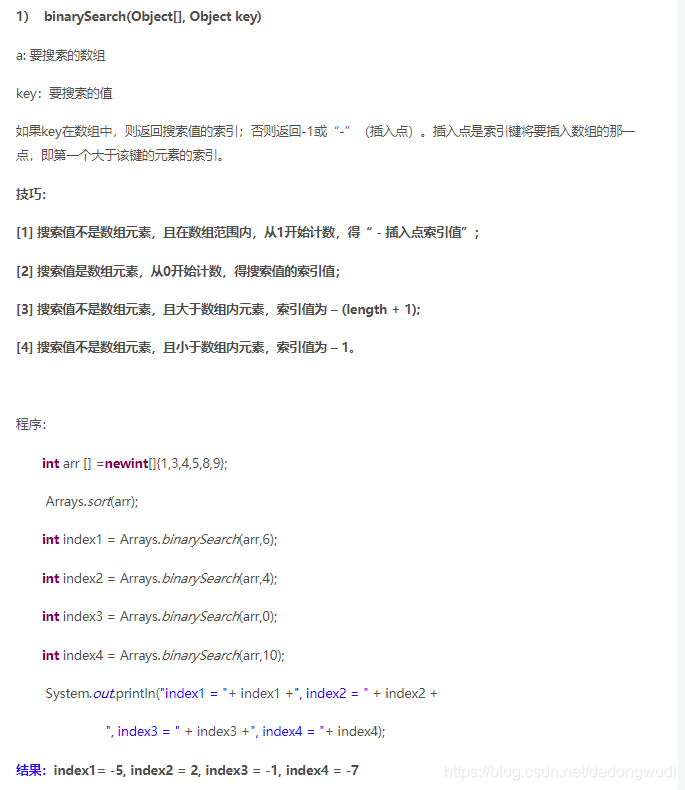
转载链接：https://leetcode-cn.com/problems/minimum-size-subarray-sum/solution/chang-du-zui-xiao-de-zi-shu-zu-by-leetcode-solutio/
参考链接https://leetcode-cn.com/problems/minimum-size-subarray-sum/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-43/
参考链接：https://blog.csdn.net/cxhply/article/details/49423501