【问题描述】[中等]

【解答思路】

1. 暴力 （超时）

时间复杂度：O(N^2) 空间复杂度：O(1)

public List<Integer> countSmaller(int[] nums) {List<Integer> ans =  new ArrayList<Integer>();int n = nums.length;if(n==0){return ans;}for(int i=0;i<n-1;i++ ){int num=0;for(int j =i;j<n;j++ ){if(nums[j]<nums[i]){num++;}}ans.add(num);}//最后一个必为 0ans.add(0);return ans;}

2. 归并排序+索引数组

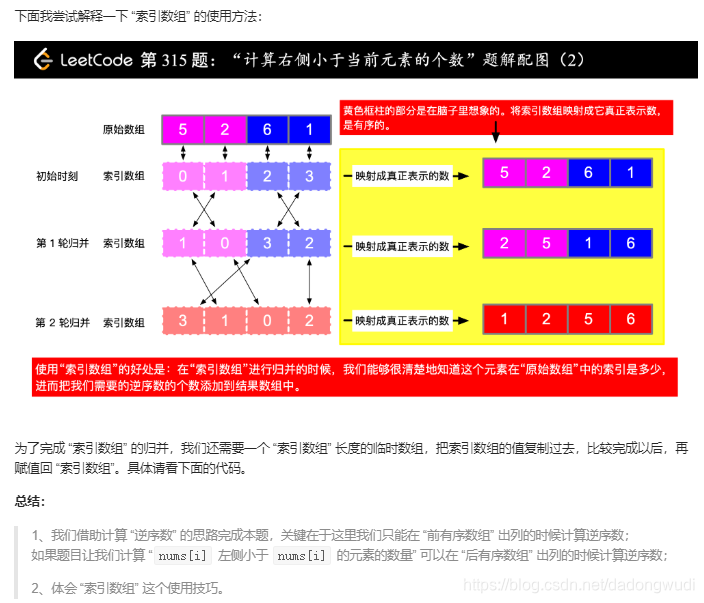
时间复杂度：O(NlogN) 空间复杂度：O(N)

import java.util.ArrayList;
import java.util.List;public class Solution {private int[] temp;private int[] counter;private int[] indexes;public List<Integer> countSmaller(int[] nums) {List<Integer> res = new ArrayList<>();int len = nums.length;if (len == 0) {return res;}temp = new int[len];counter = new int[len];indexes = new int[len];for (int i = 0; i < len; i++) {indexes[i] = i;}mergeAndCountSmaller(nums, 0, len - 1);for (int i = 0; i < len; i++) {res.add(counter[i]);}return res;}/*** 针对数组 nums 指定的区间 [l, r] 进行归并排序，在排序的过程中完成统计任务** @param nums* @param l* @param r*/private void mergeAndCountSmaller(int[] nums, int l, int r) {if (l == r) {// 数组只有一个元素的时候，没有比较，不统计return;}int mid = l + (r - l) / 2;mergeAndCountSmaller(nums, l, mid);mergeAndCountSmaller(nums, mid + 1, r);// 归并排序的优化，同样适用于该问题// 如果索引数组有序，就没有必要再继续计算了if (nums[indexes[mid]] > nums[indexes[mid + 1]]) {mergeOfTwoSortedArrAndCountSmaller(nums, l, mid, r);}}/*** [l, mid] 是排好序的* [mid + 1, r] 是排好序的** @param nums* @param l* @param mid* @param r*/private void mergeOfTwoSortedArrAndCountSmaller(int[] nums, int l, int mid, int r) {// 3,4  1,2//[left,mid],[mid+1,right]有序for (int i = l; i <= r; i++) {temp[i] = indexes[i];}int i = l;int j = mid + 1;// 左边出列的时候，计数for (int k = l; k <= r; k++) {//[left,mid]用完了，没有与[j,right]组成逆序的元素了if (i > mid) {indexes[k] = temp[j];j++;}//[mid+1,right]用完了，每个[i,mid]中的元素都能与[mid+1,right]成逆序else if (j > r) {indexes[k] = temp[i];i++;// 此时 j 用完了，[7,8,9 | 1,2,3]// 之前的数就和后面的区间长度构成逆序counter[indexes[k]] += (r - mid);} //所有小于temp[i]映射的元素，即[mid+1,j-1]中的元素成逆序else if (nums[temp[i]] <= nums[temp[j]]) {indexes[k] = temp[i];i++;// 此时 [4,5, 6   | 1,2,3 10 12 13]//           mid          j// //(j-1)-(mid+1)+1 = j-mid-1counter[indexes[k]] += (j - mid - 1);}//严格小于temp[i]映射的元素，移动j else {// nums[indexes[i]] > nums[indexes[j]] 构成逆序indexes[k] = temp[j];j++;}}}public static void main(String[] args) {int[] nums = new int[]{5, 2, 6, 1};Solution solution = new Solution();List<Integer> countSmaller = solution.countSmaller(nums);System.out.println(countSmaller);}
}

【总结】

1. “归并排序” 的细节

1、如果 “前有序数组” 和 “后有序数组” 直接合并的时候，就有序，就不必归并；

2、在 “归并” 的时候，全局使用一个临时存储数组，而不必每一个归并都新建临时的存储空间。

2.出列一个元素的时候，马上得到右边比自己小的元素的个数，是通过不同的指针之间的距离得到的。

在编码的时候，建议在草稿纸上写写画画，用具体的数值带进去，才能确保你计算的指针之间的距离正确。

3.如果你写过 “逆序数” 的计算的代码，你就会发现，“逆序数” 的计算可以在 “前有序数组” 元素出列的时候计算逆序数，也可以在 “后有序数组” 元素出列的时候计算逆序数，你可以比较一下它们在编码时候的不同之处。

转载链接：https://leetcode-cn.com/problems/count-of-smaller-numbers-after-self/solution/gui-bing-pai-xu-suo-yin-shu-zu-python-dai-ma-java-/