以HDU_1542 Atlantis 题为例

线段树和扫描线是这么结合的

    线段树统计的是有效区间段的长度 也就是扫描线 当前扫描到的区间段是哪一个
    什么意思 比如当前在哪一个段扫描 那么线段树中的t[1]中的len就是多长
    线段树一般情况下是一个后序遍历先把孩子节点的信息 更新后 再拿孩子节点的信息回来更新自己

    一旦取消这个线段 遇到了出边 那么就把这个点的覆盖情况置空 然后让这个点的信息为左右两个孩子的信息 统计
    如果这个时候左右两个孩子还有边的信息 那么依然会反馈回来 如果没有 那么这个线段就会置零


    总的来说 线段树统计的就是当前扫描时段真正的有效长度是多少
    如何通过线段树去统计？
    以离散化横坐标为例
    线段树每个叶子节点统计的都是我们所有出现过的从小到大的离散化后的x坐标顺序下标
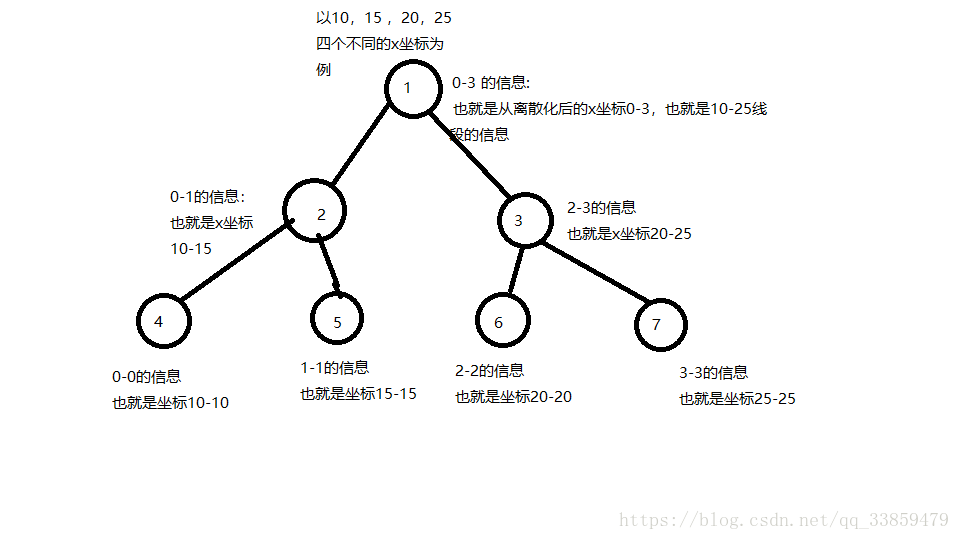
    比如一共出现了10 15 20 25四个x坐标 由于我们离散化的是横坐标 也就是要拿横坐标建树
    也就是这四个点分别对应0 1 2 3 四个点
    把线段树建成了
    那么每次我们扫描到一个线段 就到线段树中去更新这个线段
    什么意思？ 就是按照这个线段是出边还是入边
    如果是矩形入边 那么就把这个线段拿到线段树中去 我们不是已经把线段树按照对应x左边建好了吗
    那么现在遇到一个入边 按照我们之前说的线段树需要维护的东西————“当前扫描的线段所在的矩形的有效宽度”
    我们需要让线段树明白现在的有效宽度是不是变化了
    也就是把这个变得起始坐标 结束坐标搞下来 更新到线段树中
    这样我们到时候一查线段树的有效宽度 然后再用高度做一下差
    就知道当前扫描矩形的有效面积是多少了
    那么我们拿到当前边的两个坐标 去线段树中更新
    如果这个区间段在线段树中没有标记过 那么就去标记
    标记后反馈给父节点
    不断的反馈 最后父节点得到了当前状态下的有效宽度

    那么如果当前边是个出边 也就是有可能需要减少

    依然是拿到线段树中 把宽度取消

    当我们遍历了扫描方向上的所有的边 也就是把每一块的面积都累加了起来 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 110;
struct node{int xx;double len;int l,r;
}t[maxn<<3];
double x[maxn<<2];
int xtot;
struct edge{double l,r,h;int xx;edge(){}edge(double a,double b,double c,int cover):l(a),r(b),h(c),xx(cover){}bool operator<(const edge &E){return h<E.h;}
}e[maxn<<2];
int etot;
bool cmp(int a,int b){return a<b;
}
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
void build(int l,int r,int rt){t[rt].l = l;t[rt].r = r;t[rt].xx = t[rt].len = 0;if(l==r)return;int mid = l+r>>1;build(lson);build(rson);
}
void pushup(int now){if(t[now].xx){t[now].len = x[t[now].r+1]-x[t[now].l];}else if(t[now].l==t[now].r){t[now].len=0;}else {t[now].len = t[now<<1].len+t[now<<1|1].len;}
}void update(int l,int r,int rt,int val){if(t[rt].l==l&&t[rt].r==r){t[rt].xx += val;pushup(rt);return;}int mid = t[rt].l+t[rt].r>>1;//*****if(r<=mid)update(l,r,rt<<1,val);else if(l>mid)update(l,r,rt<<1|1,val);else{update(l,mid,rt<<1,val);update(mid+1,r,rt<<1|1,val);}pushup(rt);
}
int main()
{int n,test=0;while(scanf("%d",&n),n){double x1,x2,y1,y2;test++;for(int i=1;i<=n;i++){scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);e[etot++] = edge(x1,x2,y1,1);e[etot++] = edge(x1,x2,y2,-1);x[xtot++] = x1;x[xtot++] = x2;}sort(e,e+etot);sort(x,x+xtot);xtot = unique(x,x+xtot)-x;//离散化x坐标double ans =0;build(0,xtot-1,1);for(int i=0;i<etot;i++){int l = lower_bound(x,x+xtot,e[i].l)-x;int r = lower_bound(x,x+xtot,e[i].r)-x-1;//区间这里并不是完全包含比如10，15，20，25 的区间 查询10-15 那么去查的就是10-10//什么意思 因为线段树仍然是离散的统计结构 仍然还是按照起点查询区间线段update(l,r,1,e[i].xx);ans+=(e[i+1].h-e[i].h)*t[1].len;}printf("Test case #%d\nTotal explored area: %.2f\n\n",test,ans);etot = 0;xtot = 0;}return 0;}