本系列是七月算法机器学习课程笔记

1 特征工程与意义

特征工程做的事情是从数据中抽取出来的，对结果预测有用的信息。
特征工程是使用专业背景知识和机器学习技巧处理数据，使得特征能在机器学习算法上发挥更大的作用。

要提升机器学习的效果可以有三个途径：
1 选择一个合适的模型，模型越简单越好
2 编码技能和机器学习技能，能够通过调参提升效果。这个提升效果大概在千分之几的级别。
3 了解业务，通过抽取特征提升效果。这个提供效果大概在百分之几的级别。

2 数据与特征处理

2.1数据采集

在数据采集阶段需要考虑哪些数据对最后的结果有帮助
这些数据能不能采集到
在预测阶段一般是实时在线的，这个时候采集这些数据是否能实时获取，不能实时获取或者代价很大的数据，不能使用

例如：现在设计一个算法，预测同学学习课程的兴趣程度。可以考虑采集哪些数据呢？
同学们学习课程的兴趣程度，可能跟老师、课程、同学相关。
与老师相关的指标可能有：性别、声音、学历。
与课程相关的指标可能有：课程内容、难易程度、是否与工作相关。
与同学相关的指标可能有：有无数学基础、学历、目前就职状态、找工作计划。

设计好特征之后就可以采集数据了。

2.2 数据清洗

采集后的数据需要清洗，否则就是garbage in , garbage out，（喂了垃圾数据，出来的模型也是垃圾的）

数据清洗可以从以下角度考虑。

1 单维度可信程度
例如一个人身高3米，一个实验室每个月买墩布10万元…
在数据清洗过程中可以根据情况去掉前百分之一和大于99%的那部分数据。

2 组合或统计属性判定
用常识解决异常值。例如在判断用户是否会买篮球的模型中，数据中有85%的女性样本。就不符合常识。

3 补齐缺省值

2.3 数据采样

在遇到正负样本数量悬殊的情况下应该怎么处理？
1 如果正负样>>负样本，且量都很大，可以使用下采样的方式解决。以负样本的数量为准，通过随机抽样的方式从正样本采集几乎同样数量的样本。还可以从正样本中通过分层抽样的方式重新采集样本。

这里补充一下下采样的时间。先对原始数据集做训练集和测试集的拆分。之后对训练集中的样本多的分类做下采样。这是看见老师讲的案例中是这样的。原因不清楚。我想大概是这样可以在评估模型的时候因为测试集中的正样本更具代表性，模型准确度也会更可靠吧。

假如一个数据集中正样本 800，负样本 100。
先分数据集训练集、测试集，测试集占比20%。 测试中 正样本 160,负样本
20；训练集中 正样本640,负样本80。再下采样，正样本80，负样本80。
用此训练出的模型，在评估模型的时候这样本是160个，相对来说更客观一点。
先下采样 正样本100，负样本100
再分训练集、测试集，20% 测试集中 正样本 20，负样本20，训练集中 正样本80，负样本80。
这里测试集中正样本数量只有20。相比前一个方法，缺失一点客观性。
大概是这样吧。

例如我前段时间做网页是否是列表页的判断。是列表页的数据量＜不是列表页的数量。那我就从不是列表页的数量的样本中按照站点分组。例如我需要300个样本，有5个站点，就每个站点随机抽取60个样本组成新的不是列表页的样本集。

2 如果正样本>>负样本，且量都不大，可以使用过采样的方式解决。对负样本的数据重复多份，或者样本是图片的话可以通过旋转，缩放等方式产生新的样本数据。

在一些场景下还可以使用SMOTE算法造出一些数据。

2.4 特征处理

特征值的类型有：数值型、类别型、时间类、文本型、统计型、组合特征。下面分别描述各类特征的处理方式。

2.4.1 数值型

1 数值型特征幅度调整
在一个模型中房间数量的值在[2,10]之间，房屋面积的值在[70,500]之间。这种幅度不同的特征值，幅度大的特征会对模型有更大的影响。所以模型效果不会很好。需要调整到同一幅度内。

我们可以将特征值调整在[0,1]范围内：MinMaxScaler。计算方式：$d=\frac{d-min}{max-min}$

我们也可以对特征值对标准化处理：StandScaler。计算方式:$d=\frac{d-mean}{标准差}$

2 可以通过log等函数，让特征值的数据域发生变化

3 计算特征值的统计值

统计值包含：max、min、mean、std。这可以通过pandas的describe方法获得。

4 离散化
首先说明为什么要做离散化。现在要用逻辑回归做一个地铁上是否让座的模型。其中一个特征值是年龄。
逻辑回归的方程是$p=\frac{1}{1+e^{-wx}}$
一般情况下当遇到小宝宝或者老人会让座。上面的函数中，假设w为正，x越大，p越大。这样的话，就不能覆盖年龄小的情况。假设w为负，x越小，p越大，这样的话，就不能覆盖年龄大的情况。
这个时候，我们就需要对年龄做离散化。这是因为我们没有对特征做进一步的细分。我们可以分为[0,6],[6-60],[60]三个特征。三个特征，三个权重，可以各自调整不受制约。

再补充一个离散化的例子。例如在共享单车模型中，有一个特征是一星期的第几天。通过观察我们发现周一到周五会有两个使用高峰期，周六周日是一个使用高峰期。为了将这个特点描述出来，我们就需要对这个特征做离散化，分为两类：工作日和周末。

接着说明怎么做离散化，分割的标准点在哪里。
一种方法是等距切分。例如要分10分，最大值和最小值差距是100，那就每隔10，做一次分割。pandas函数是qcut。这种情况对于分布均匀的特征值比较适合。
一种方法是将样本平均分配到不同的桶中。pandas函数是cut。

5 柱状分布
统计不同value的值的个数。例如样本中的年龄特征：0岁的10个，5岁的10个，20的30个，24岁的1个…

2.4.2 类别型

类别型的特征，例如衣服的颜色有红、黄、蓝、绿。这就是一个类别型的特征。还有每个星期的第几天也是类别型。

1 one-hot编码
对于衣服的颜色有红、黄、蓝、绿，我们用什么表示呢？可以使用1、2、3、4分别表示四种颜色。但是这样的话，当w为正的时候，绿色比红色对结果的影响大。当w为负的时候，红色笔绿色对结果的影响大。这是没有道理的。这四种颜色应该是平等的。

在工程中使用one-hot编码，也称哑变量。我们在原来的数据集后面增加4列：是否红色、是否黄色、是否蓝色、是否绿色。对于一条数据只可能在其中一列值为1，其他列值为0。

2 hash技巧
例如在每一篇新闻中会出现很多词。整个数据集中会有很多词。每一遍文章中出现的词置为1。

这样处理的问题是矩阵是稀疏的，维度很高。可以使用hash桶的技巧。在数据集对每篇新闻做了分类，我们可以得到每个分类的词汇集合。例如可以知道财经类新闻、体育类新闻、娱乐类新闻的词汇集。一篇文章中出现的词属于哪个桶就在这个桶的value值+1。

例如doc1，在财经类新闻集中出现了3个词汇，体育类中出现了2个词汇。

3 histogram映射

例如数据集中的爱好有：足球、散步、看电视剧。这个爱好在性别中的分布是怎样的呢？
男：[1/3,2/3,0] 女：[0,1/3,2/3]
这个爱好在年龄中的分布是怎样的呢？
21:[1,0,0] 22:[0,0,1]…

得到这些数据之后怎么用呢？例如爱好在性别中的分布，得到之后，在原数据集后， 增加6列：足球男性分布、散步男性分布、看电视剧男性分布、足球女性分布、散步女性分布、看电视剧女性分布。每一条数据的这6个值都等于：1/3,2/3,0,0,1/3,2/3。这样的特征可能对于模型有作用，但不一定。

2.4.3 时间型

时间型特征可以看做连续值，也可以看做是离散值。
如果计算的是持续时间（单页面浏览时长）、间隔时长（上次购买/点击离现在的时长）的时候是连续值。

离散值对应的特征：
年
月
一年中第几个星期
一年中第几个季度
一月中第几个星期
一天中的哪个时段
一周的第几天
工作日/周末
距离节假日的天数

2.4.3 文本型

1 词袋模型
CounterVectorizer()
得到一个稀疏向量

2 n-gram
解决 李雷喜欢韩梅梅 韩梅梅喜欢李雷 这种词的位置关系问题
CounterVectorizer(ngram_range=(1,2),token_pattern=’\b\w+\b’,min_df=1)

3 tf-idf
$TF(t)=\frac{词t在当前文本中的出现次数}{词t在总数据集中的出现次数}$

$IDF(t)=ln(\frac{总文档数}{含t的文档数})$

$TF-IDF=TD(t)\ast IDF(t)$

3 word2vec
得到一个稠密向量

2.4.4 统计特征

例如在判断用户是否会购买的模型中：
1 购物车转换率=>用户维度的统计特征
2 对不同商品点击/收藏/购买的总计=>商品维度的特征
3 删除掉30天内从来不买东西的人=>按规则清洗
…

统计特征主要包含有：
1 加减平均：例如商品高于平均价多少，用户连续登陆天数超过平均值多少…
2 分位线：商品价格位于售出商品价格的多少分位线
3 次序性：排在第几位
4 比例类：电商中，好中差评的比例

组合特征
组合特征是把任意两个特征拼接在一起。只有这一条数据中两个特征都为1，这个值才为1，否则为0。

例如随意组合两个特征：用户id_category: 1001_女裙,1001_男士牛仔裤,1002_男士牛仔裤??

也可以通过决策树学出一棵树模型，按照树模型中的全部或者部分路径做组合。

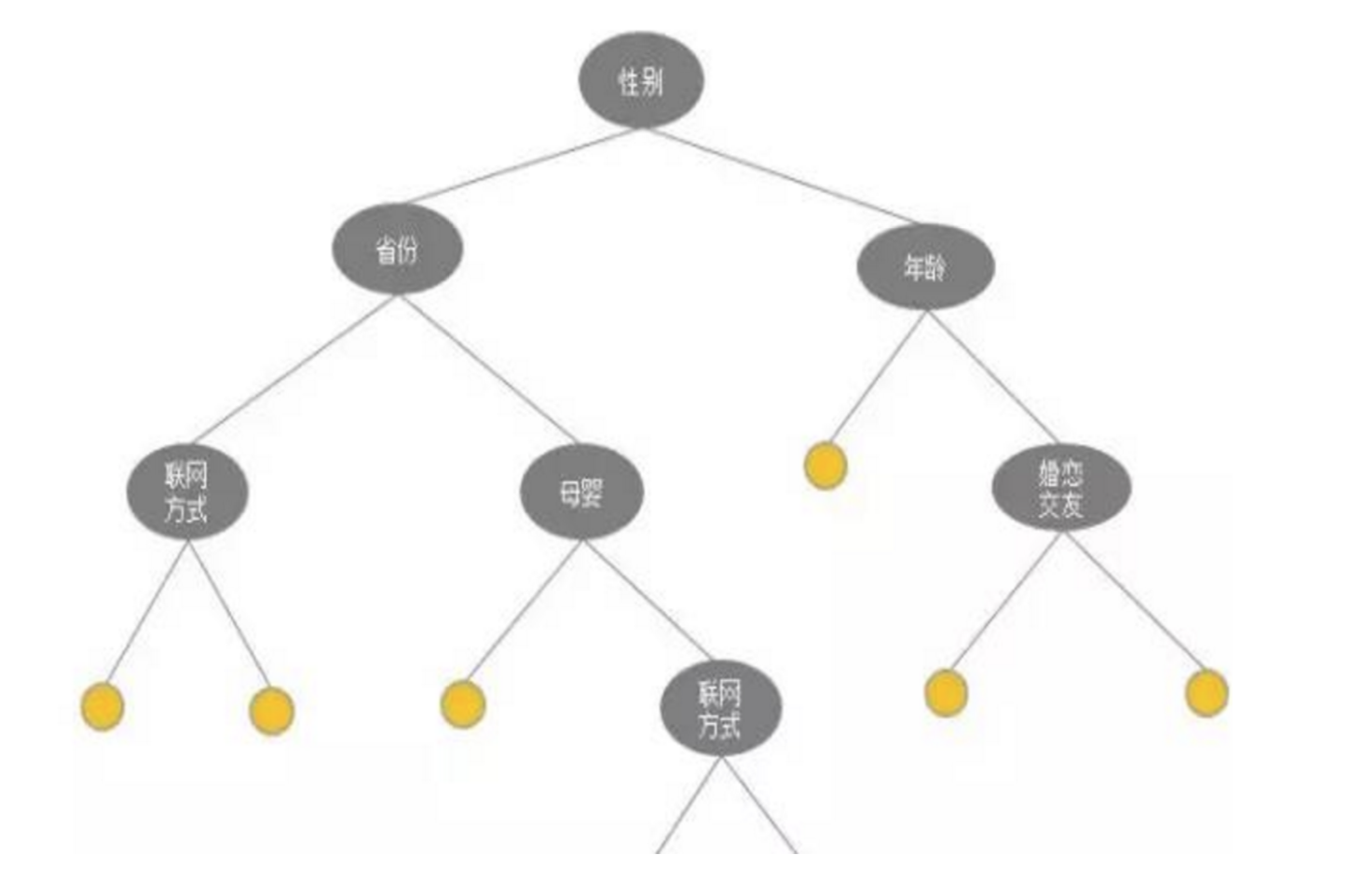
例如组合特征是:男士_上海，男士_北京，女士_上海…

3 特征选择

3.1 为什么做特征选择

因为有些特征是冗余的，有几个特征之间相关度很高，消耗计算资源。
有些特征是噪声，对结果没有影响或者产生不好的影响。

特征选择不同于降维：特征选择是踢掉原本特征中和结果预测关系不大的，而降维是做特征的计算组合构成新的特征。
降维确实也能解决一定的高纬度的问题。

3.2 特征选择的方法

3.2.1 过滤型

评估单个特征和结果之间的相关度，留下Top 相关的特征部分。
可以使用pearson相关系数、互信息等测量相关度。
缺点：是没有考虑到特征之间的关联作用，可能把有用的关联特征过滤掉。
相关python包：SelectKBest

3.2.2 包裹型

典型的包裹型算法是递归特征删除算法（recursive feature elimination algorithm）

具体做法是：
1 用全量特征跑一个模型
2 根据线性模型的系数，删掉5-10%的特征，再跑一次，观测准确率的变化。
3 如果准确率没有明显变化，重复2。如果有大的下滑就停止。

相关python包：sklearn.feature_selection.RFE
这用在稠密矩阵中效果比较好。

3.2.3 嵌入型

最常见的方式是用正则化来做特征选择。
在LR模型中，L1正则化能够起到截断作用。在3-5亿维度的模型中，用L1正则化最后可以剩下2-3千万的维度。意味着其他维度都不重要。
这在LR和线性SVM中都起作用。
在这稀疏矩阵中效果比较好。

第二种和第三种方法用的比较多。