加qq1126137994 一起学习更多技术！！！

有一个矩阵map，它每个格子有一个权值。从左上角的格子开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，返回所有的路径中最小的路径和。

给定一个矩阵map及它的行数n和列数m，请返回最小路径和。保证行列数均小于等于100.

测试样例：
[[1,2,3],[1,1,1]],2,3
返回：4

分析
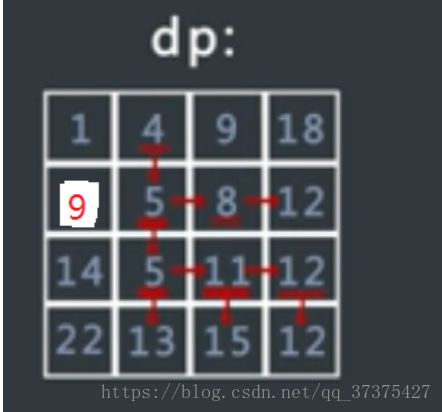
假设矩阵m的大小为M*N,行数为M，列数为N，生成大小和m一样的矩阵dp，行数为M，列数为N，dp[i][j]的值等于m矩阵从左上角，也就是（0,0）
走到（i，j）位置的最小路径和。

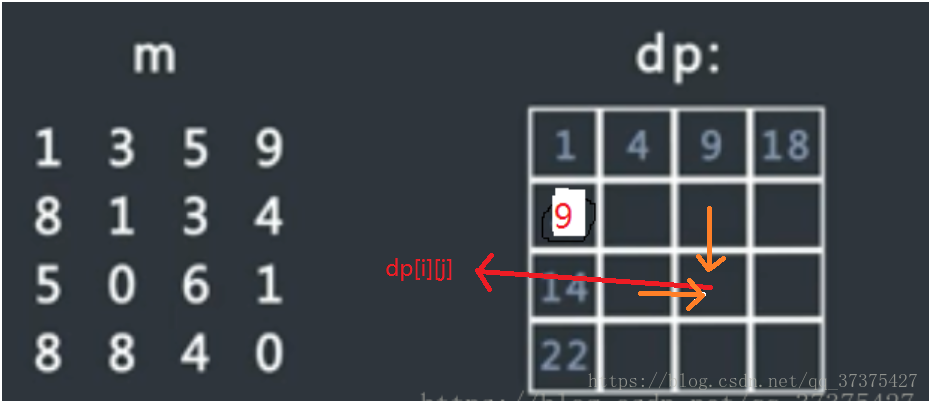
第一行与第一列，通常都是可以通过一个循环求出来的：
第一行的值：只能是从左往右走，路径最小值为前一个方格的路径最小值加上本方格所对应的权值，即dp[0][j] = dp[0][j-1]+m[i][j]
第一列的值：只能是从上往下走，路径最小值为上一个方格的路径最小值加上本方格所对应的权值；即dp[i][0] = dp[i-1][0]+m[i][j]

那么除了第一行和第一列的值，其他部分的值为（只能是从上面过来，或者从左边过来）：

最终，右下角的值，就为我们所要求的值：

实现代码如下：

class MinimumPath {
public:int R_min(int m,int n){if(m>=n)return n;elsereturn m;}int getMin(vector<vector<int> > map, int n, int m) {// write code here//额外开辟一个dp矩阵，并将dp矩阵所有值初始化为0vector<vector<int> > dp(n,vector<int>(m,0));//矩阵的第一个空格的值就等于map矩阵的第一个值的本身dp[0][0]= map[0][0];//先求第一行的值for(int j=1;j<m;j++){dp[0][j] = dp[0][j-1] + map[0][j];}//再求第一列的值for(int i=1;i<n;i++){dp[i][0] = dp[i-1][0] + map[i][0];}//最后求其他行的值for(int i=1;i<n;i++){for(int j=1;j<m;j++){dp[i][j]=R_min(dp[i-1][j]+map[i][j],dp[i][j-1]+map[i][j]);}}return dp[n-1][m-1];}
};

以上程序，求两个数的最小值并返回是可以不写的。可以直接用库函数min();但是我是因为不熟悉C++的库函数，所以自己写了一个，影响不大！！！

以上的分析思路，依然是：先解决子问题！！！何为子问题？就是我们把所要求的整体的问题，化简到最简单的情况，比如，上面的题，我们要求走到最右下角的路径的最小值，那么我们就化简，化简到，整个矩阵为1个方格，2个方格，3个方格，4个方格…… 时的最短路径的求解，然后，前面的子问题求出来了，我们会发现，通过前面子问题的整合，可以求得整体问题，也就是最终，我们可以求得最右下角的值，这也避免了，很多的重复计算，更加避免了递归所带来的复杂的运算顺序！！！