概率论的公理结构

样本点

一个随机事件出现的可能的结果叫做样本点。

类比平面几何，线、面、体也是由点组成的集合，研究的是点线面关系及性质，同样样本点也是组成事件（集合）的材料，是集合的基本元素，把这些样本点用各种形状组合起来形成集合，站在集合论的基础上讨论研究。

代数

设 $\Omega$ 是样本空间， $\boldsymbol{F}$ 是由 $\Omega$ 的一些子集所构成集合簇，如果 $\boldsymbol{F}$ 满足如下条件：

$i)$ $\Omega\in \mathbf{F}$ ；

$ii)$ 若 $A\in \mathbf{F}$ ，则 $\overline{A}\in \mathbf{F}$ ；

$iii)$ 若 $A_{i}\in \mathbf{F}(i=1,2,...n)$ ，则 $\bigcup_{i=1}^{n} A_{i}\in \mathbf{F}$ ；

则称 $\boldsymbol{F}$ 为代数。

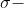$\sigma -$ 代数

设 $\Omega$ 是样本空间， $\boldsymbol{F}$ 是由 $\Omega$ 的一些子集所构成集合簇，如果 $\boldsymbol{F}$ 满足如下条件：

$i)$ $\Omega\in \mathbf{F}$ ；

$ii)$ 若 $A\in \mathbf{F}$ ，则 $\overline{A}\in \mathbf{F}$ ；

$iii)$ 若 $A_{i}\in \mathbf{F}(i=1,2,...\infty )$ ，则 $\bigcup_{i=1}^{\infty } A_{i}\in \mathbf{F}$ ；

则称 $\boldsymbol{F}$ 为 $\sigma -$ 代数。

容易证明，如果样本空间是有穷的，则它的任何代数也必是 $\sigma -$ 代数。

可测空间

把任一样本空间 $\Omega$ ，以及由 $\Omega$ 的子集所组成的一个 $\sigma -$ 代数 $\boldsymbol{F}$ 写在一起，记为 $(\Omega , \mathbf{F})$ ，称为具有 $\sigma -$ 代数结构的样本空间，或简称为可测空间。

概率

设 $(\Omega , \mathbf{F})$ 是可测空间，对每一集 $A\in \mathbf{F}$ ，有一实数与之对应，记为 $P(A)$ （因此在 $\boldsymbol{F}$ 上定义了一个集函数 $P$ ），如它满足下面三个条件：

$i)$ 对每一 $A\in \mathbf{F}$ ，有 $0\leqslant P(A) \leqslant 1$ ；

$ii)$ 对必然事件 $\Omega$ ，有 $P(A)=1$ ；

$iii)$ （完全可加性）对任意 $A_{i} \in \mathbf{F}(i=1,2,...)$ ， $A_{i} \bigcap A_{j} = \phi \ (i \neq j)$ ，恒有

$P(\bigcup_{i=1}^{\infty} A_{i}) = \sum_{i=1}^{\infty} P(A_{i})$

则称实值集函数 $P$ 为 $(\Omega , \mathbf{F})$ 上的概率， $P(A)$ 就称为事件 $A$ 的概率。

上面几个概念的层次关系是：设 $\Omega$ 是一样本空间， $\bold{F}$ 为 $\Omega$ 的 $\sigma-$ 代数， $P$ 为 $\bold{F}$ 上的概率，我们称具有上述结构的样本空间为概率空间，记为 $(\Omega, \bold{F}, P)$ 。

随机变量

设 $(\Omega, \bold{F}, P)$ 是一个概率空间，对于样本点 $\omega \in \Omega$ ， $\xi(\omega)$ 是一个取实值的单值函数；若对于任一实数 $x$ ， $\left \{ \omega: \xi(\omega) < x \right \}$ 是一随机事件，亦即 $\left \{ \omega: \xi(\omega) < x \right \} \in \bold{F}$ ，则称 $\xi(\omega)$ 为随机变量。