目录

 

为什么需要复杂度分析？

大 O 复杂度表示法

时间复杂度分析

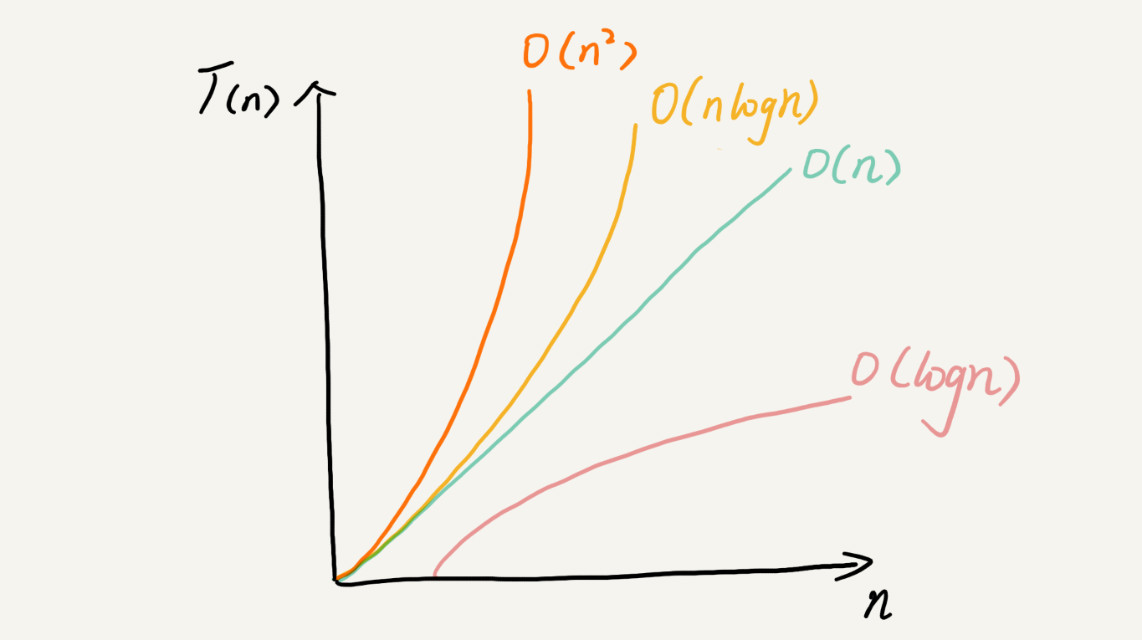
几种常见时间复杂度

空间复杂度分析

---

为什么需要复杂度分析？

事后统计法：代码跑一遍，通过统计、监控，就能得到算法执行的时间和占用的内存大小。这种统计方法有非常大的局限性。

1. 测试结果非常依赖测试环境
2. 测试结果受数据规模的影响很大

因此，我们需要一个不用具体的测试数据来测试，就可以粗略地估计算法的执行效率的方法。

大 O 复杂度表示法

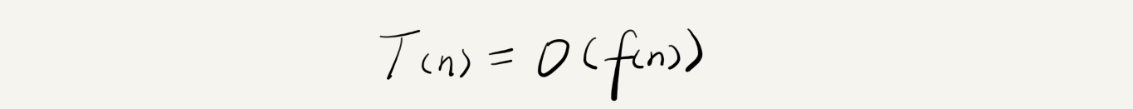
T(n)表示算法的执行时间，n表示数据规模的大小，f（n）表示每行代码执行的次数总和。公式中的 O，表示代码的执行时间 T(n) 与 f(n) 表达式成正比。

大 O 时间复杂度实际上并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势，所以，也叫作渐进时间复杂度（asymptotic time complexity），简称时间复杂度。

时间复杂度分析

如何分析一段代码的时间复杂度？有三个比较实用的方法

1. 关注循环次数最多的一段代码
2. 加法法则：总复杂度等于量级最大的那段代码的复杂度
3. 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

几种常见时间复杂度

1.、O(1):一般情况下，只要算法中不存在循环语句、递归语句，即使有成千上万行的代码，其时间复杂度也是Ο(1)。

2、O(logn)、O(nlogn)对数阶时间复杂度非常常见，同时也是最难分析的一种时间复杂度。我通过一个例子来说明一下。

3、O(m+n)、O(m*n)：代码的复杂度由两个数据的规模来决定

空间复杂度分析

空间复杂度全称就是渐进空间复杂度（asymptotic space complexity），表示算法的存储空间与数据规模之间的增长关系

我们常见的空间复杂度就是 O(1)、O(n)、O(n2 )，像 O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到。而且，空间复杂度分析比时间复杂度分析要简单很多。所以，对于空间复杂度，掌握刚我说的这些内容已经足够了。