思考题
二叉树有哪几种存储方式？什么样的二叉树适合用数组来存储？
树（Tree）
- 根节点：没有父节点的节点
- 叶子节点或者叶节点：没有子节点的节点叫做
树的高度、深度、层：
举例说明：
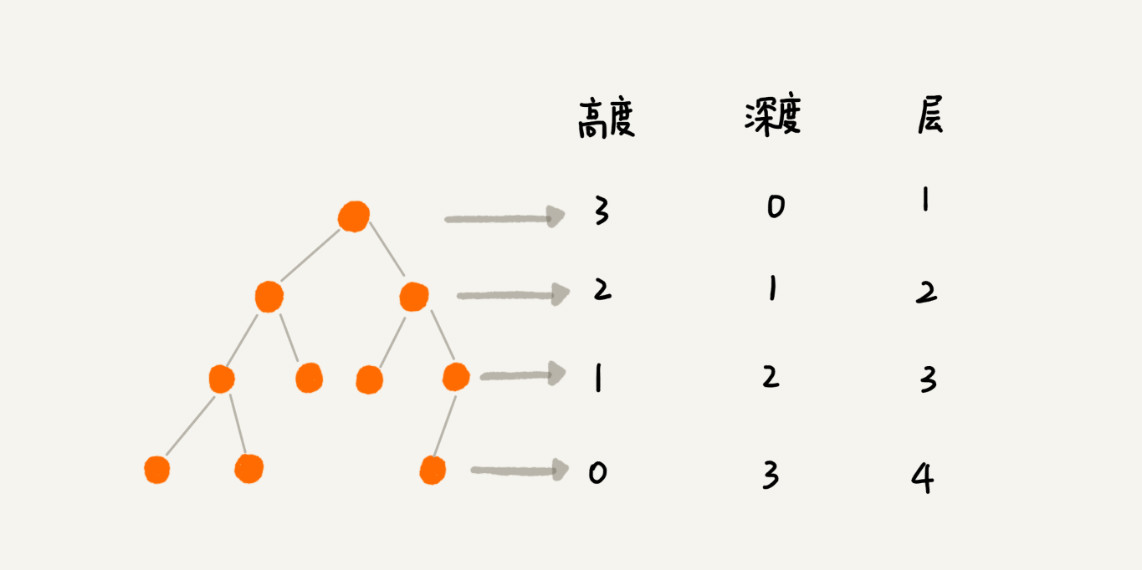
- 生活中，“高度”这个概念，其实就是从下往上度量，比如我们要度量第 10 层楼的高度、第 13 层楼的高度，起点都是地面。所以，树这种数据结构的高度也是一样，从最底层开始计数，并且计数的起点是 0。
- “深度”这个概念在生活中是从上往下度量的，比如水中鱼的深度，是从水平面开始度量的。所以，树这种数据结构的深度也是类似的，从根结点开始度量，并且计数起点也是 0
- “层数”跟深度的计算类似，不过，计数起点是 1，也就是说根节点位于第 1 层。
二叉树
定义：每个节点最多有两个“叉”，也就是两个子节点，分别是左子节点和右子节点。二叉树并不要求每个节点都有两个子节点，有的节点只有左子节点，有的节点只有右子节点。
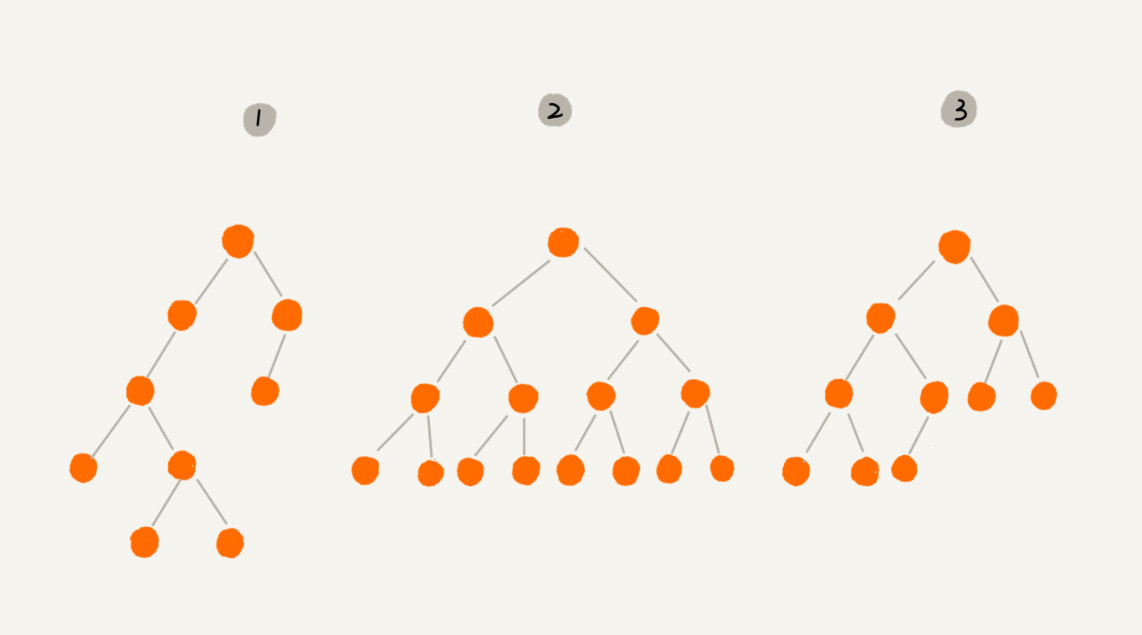
满二叉树：叶子节点全都在最底层，除了叶子节点之外，每个节点都有左右两个子节点
完全二叉树：叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大
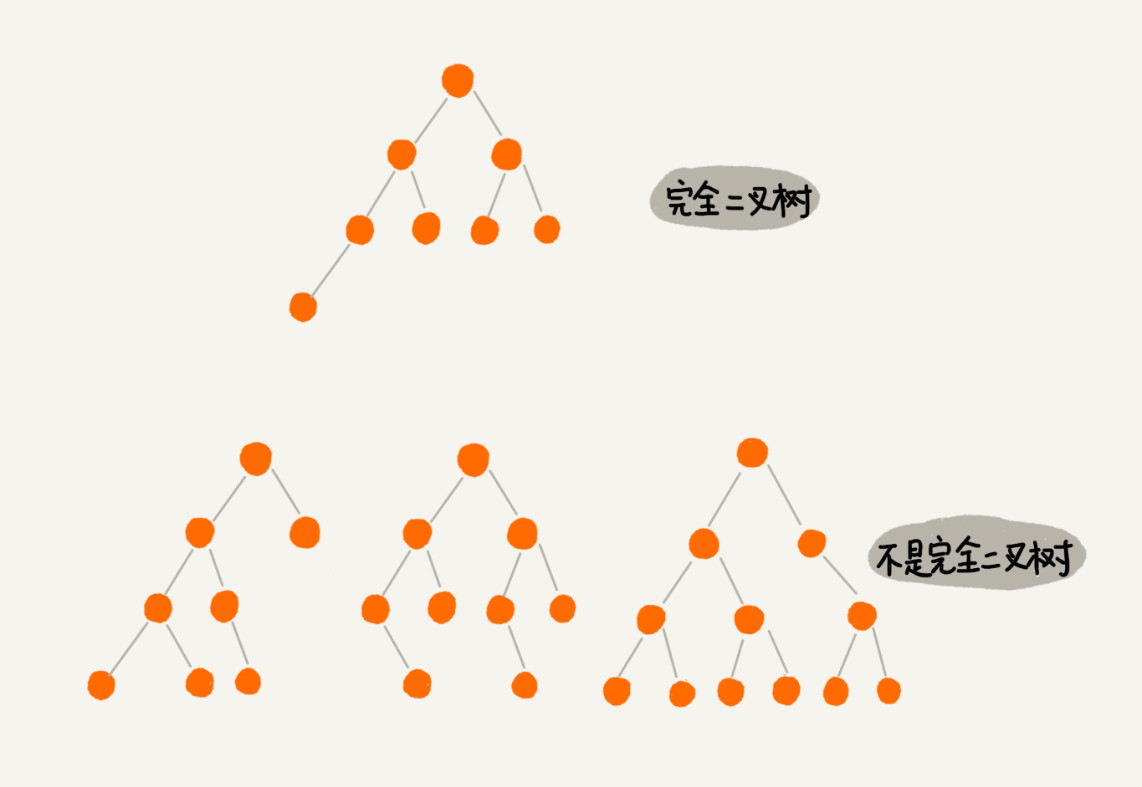
为什么要单独提出一种完全二叉树
首先了解如何表示一颗二叉树？存储一棵二叉树，我们有两种方法，一种是基于指针或者引用的二叉链式存储法，一种是基于数组的顺序存储法。
1、链式 存储：常用的存储方式。每个节点有三个字段，其中一个存储数据，另外两个是指向左右子节点的指针。我们只要拎住根节点，就可以通过左右子节点的指针，把整棵树都串起来
2、基于数组的顺序存储法。我们把根节点存储在下标 i = 1 的位置，那左子节点存储在下标 2 * i = 2 的位置，右子节点存储在 2 * i + 1 = 3 的位置。以此类推，B 节点的左子节点存储在 2 * i = 2 * 2 = 4 的位置，右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置。
总结：
- 如果节点 X 存储在数组中下标为 i 的位置，下标为 2 * i 的位置存储的就是左子节点，下标为 2 * i + 1 的位置存储的就是右子节点。一般情况下，为了方便计算子节点，根节点会存储在下标为 1 的位置），这样就可以通过下标计算，把整棵树都串起来。
- 一棵完全二叉树，所以仅仅“浪费”了一个下标为 0 的存储位置。如果是非完全二叉树，会浪费比较多的存储空间
- 如果某棵二叉树是一棵完全二叉树，那用数组存储最节省内存。数组的存储方式并不需要像链式存储法存储额外的左右子节点的指针。这也是为什么完全二叉树会单独拎出来的原因，也是为什么完全二叉树要求最后一层的子节点都靠左的原因。
- 堆和堆排序的时候，你会发现，堆其实就是一种完全二叉树，最常用的存储方式就是数组。
二叉树的遍历
如何打印遍历树的所有节点呢？经典的方法有三种，前序遍历、中序遍历和后序遍历。其中，前、中、后序，表示的是节点与它的左右子树节点遍历打印的先后顺序。
- 前序遍历是指，对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。
- 中序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。
- 后序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。
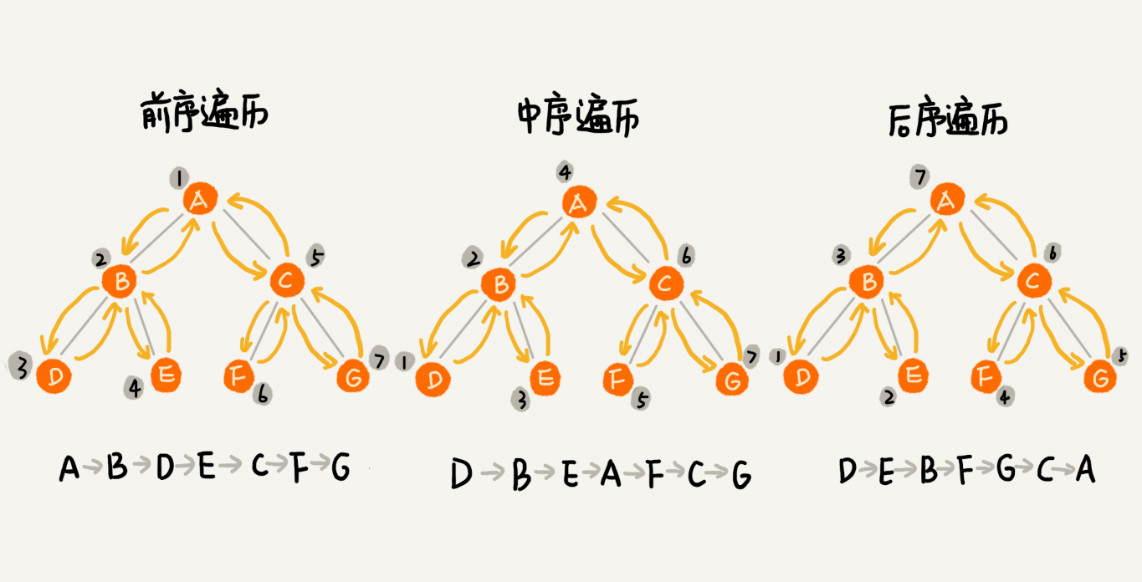
二叉树的前、中、后序遍历就是一个递归的过程。比如，前序遍历，其实就是先打印根节点，然后再递归地打印左子树，最后递归地打印右子树。写递归的关键是写出递推公式，而写出递推公式的关键是如果要解决问题A，假设子问题B\C都已经解决，再来看如何利用B\C来解决A。
前序遍历的递推公式：
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)中序遍历的递推公式：
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)后序遍历的递推公式：
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r
void preOrder(Node* root) {if (root == null) return;print root // 此处为伪代码，表示打印root节点preOrder(root->left);preOrder(root->right);
}void inOrder(Node* root) {if (root == null) return;inOrder(root->left);print root // 此处为伪代码，表示打印root节点inOrder(root->right);
}void postOrder(Node* root) {if (root == null) return;postOrder(root->left);postOrder(root->right);print root // 此处为伪代码，表示打印root节点
}二叉树遍历的时间复杂度是多少吗？前面画的前、中、后序遍历的顺序图，可以看出每个节点最多会被访问两次，遍历操作的时间复杂度跟节点的个数 n 成正比，也就是说二叉树遍历的时间复杂度是 O(n)。
