几种排序与最大K问题

图片链接

0. 链表归并和快排

链表排序常用归并，但是快排面试常出；

一定要理解归并的本质：

两步走：

1. 先切分成(有序)两部分，此处各部分都是有序的

2. 两部分有序合并

切分成两部分的最小粒度是一个元素，所以切分函数并不需要排序，排序部分在合并函数中。

public class ListNode {int val;ListNode next;ListNode() {}ListNode(int val) { this.val = val; }ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}//1. 归并
public ListNode sortList(ListNode head) {if(head==null || head.next==null)return head;ListNode fast = head,slow = head;ListNode pre = null;// 另一种写法 fast.next != null && fast.next.next != nullwhile (fast != null && fast.next != null){pre = slow;fast = fast.next.next;slow = slow.next;}if (pre != null) pre.next = null;ListNode p1 = sortList(head);ListNode p2 = sortList(slow);return merge(p1, p2);
}public ListNode merge(ListNode p1,ListNode p2){ListNode dummyHead = new ListNode(0);ListNode cur = dummyHead;while (p1 != null && p2 != null){if (p1.val < p2.val) {cur.next = p1;p1 = p1.next;} else {cur.next = p2;p2 = p2.next;}cur = cur.next;}if (p1 != null) cur.next = p1;if (p2 != null) cur.next = p2;return dummyHead.next;
}//2. 快排
public ListNode sortList2(ListNode head){if (head == null || head.next == null) return head;ListNode dummy = new ListNode(0);dummy.next = head;return partion(dummy, null);//开区间
}public ListNode partion(ListNode begin, ListNode end){ // 开区间if (begin == end || begin.next == end || begin.next.next == end) return begin;ListNode partion = begin.next; // partion的值// ListNode pre = begin.next;// 待排序的ListNode pre = begin;ListNode dummy = new ListNode(0);ListNode cur = dummy;// 排好序的while (pre.next != end) {if (pre.next.val < partion.val) {cur.next = pre.next; // 小于的接在dummy上pre.next = pre.next.next; // 把原链表中小的删除cur = cur.next;} else {pre = pre.next;}}// 将原链表(值都大于partion)接到临时链表(值都小于partion)后cur.next = begin.next;// 将临时链表插回原链表（不做这一步在对右半部分处理时就断链了）begin.next = dummy.next;partion(begin, partion);partion(partion, end);return begin.next;
}

1.快排

/*
void quickSort(int *pArray, int begin, int end) {if (begin < end) {int left = begin;int right = end;int pivot = pArray[begin];while (left < right) {while (left < right && pArray[right] >= pivot)right--;if (left < right)pArray[left++] = pArray[right];while (left < right && pArray[left] <= pivot)left++;if (left < right)pArray[right--] = pArray[left];}pArray[left] = pivot;quickSort(pArray, begin, left - 1);quickSort(pArray, left + 1, end);}
}
*/vector<int> sortArray(vector<int>& nums) {int n = nums.size();quickSort(nums, 0, n - 1);return nums;
}void quickSort(vector<int>& nums, int l, int r) {if (l >= r) {return;}int idx = rand() % (r - l + 1) + l; // 随机选一个作为我们的主元swap(nums[l], nums[idx]);int p = nums[l];int left = l, right = r;while (left < right) {while (left < right && nums[right] >= p) {right--;}nums[left] = nums[right];while (left < right && nums[left] <= p) {left++;}nums[right] = nums[left];}nums[left] = p;quickSort(nums, l, left - 1);quickSort(nums, left + 1, r);
}

2）

    public int quickSort(int[] nums,int l,int r){// 在区间随机选择一个元素作为标定点if (r > l) {int randomIndex = l + random.nextInt(r - l);swap(nums, l, randomIndex);}int p = nums[l];int j = l;for (int i = l+1;i <= r;i++){if (nums[i] > p){j++;swap(nums,j,i);}}//上述这样就保证了[l,j]都是大于等于p的，(j,r]都是小于的 l等于p l换到j处即可swap(nums,j,l);return j;}

2.归并排序

1）

public static void mergeSort(int[] arr) {sort(arr, 0, arr.length - 1);
}public static void sort(int[] arr, int L, int R) {if(L == R) {return;}int mid = L + ((R - L) >> 1);sort(arr, L, mid);sort(arr, mid + 1, R);merge(arr, L, mid, R);
}public static void merge(int[] arr, int L, int mid, int R) {int[] temp = new int[R - L + 1];int i = 0;int p1 = L;int p2 = mid + 1;// 比较左右两部分的元素，哪个小，把那个元素填入temp中while(p1 <= mid && p2 <= R) {temp[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];}// 上面的循环退出后，把剩余的元素依次填入到temp中// 以下两个while只有一个会执行while(p1 <= mid) {temp[i++] = arr[p1++];}while(p2 <= R) {temp[i++] = arr[p2++];}// 把最终的排序的结果复制给原数组for(i = 0; i < temp.length; i++) {arr[L + i] = temp[i];}
}

2）

public class MergeSort {   public static int[] mergeSort(int[] nums, int l, int h) {if (l == h)return new int[] { nums[l] };int mid = l + (h - l) / 2;int[] leftArr = mergeSort(nums, l, mid); //左有序数组int[] rightArr = mergeSort(nums, mid + 1, h); //右有序数组int[] newNum = new int[leftArr.length + rightArr.length]; //新有序数组int m = 0, i = 0, j = 0; while (i < leftArr.length && j < rightArr.length) {newNum[m++] = leftArr[i] < rightArr[j] ? leftArr[i++] : rightArr[j++];}while (i < leftArr.length)newNum[m++] = leftArr[i++];while (j < rightArr.length)newNum[m++] = rightArr[j++];return newNum;}public static void main(String[] args) {int[] nums = new int[] { 9, 8, 7, 6, 5, 4, 3, 2, 10 };int[] newNums = mergeSort(nums, 0, nums.length - 1);for (int x : newNums) {System.out.println(x);}}
}

3.冒泡排序

public static void bubbleSort(int arr[]) {int n = arr.length;// i 表示的是最后 i+1 个有序for (int i = 0; i < n - 1; i++) { for (int j = 0; j < n - 1 - i; j++) {  if (arr[j] > arr[j+1]) {int temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;}}}
}

4.插入排序

public static void sort(Comparable[] a) {// 将a[]按升序排列  i前是有序数列int N = a.length;for (int i = 1; i < N; i++) {// 将a[i]插入到 [0, i) 之中int cur = a[i];int j = i - 1;for (; j >= 0 && a[j] > cur; j--) {a[j + 1] = a[j]; // 后移}a[j + 1] = a[i];}
}

5.堆排序

优先队列手动实现

剑指 Offer II 076. 数组中的第 k 大的数字

class Solution {
public:int findKthLargest(vector<int>& nums, int k) {vector<int> arr(nums.begin(), nums.begin() + k);// build treebuild(arr);for (int i = k; i < nums.size(); i++) {// 大于树根 adjustif (nums[i] > arr[0]) {arr[0] = nums[i];adjust(arr, 0, k);}}return arr[0];}void build(vector<int>& nums) {int n = nums.size();for (int i = n / 2 - 1; i >= 0; i--) {adjust(nums, i, n);}}// 最小堆void adjust(vector<int>& nums, int i, int n) {int p = nums[i];for (int k = 2 * i + 1; k < n; k = k * 2 + 1) {if (k + 1 < n && nums[k + 1] < nums[k]) {k++;}if (nums[k] < p) {nums[i] = nums[k];i = k;}}nums[i] = p;}
};

sort和adjust，参考链接

int n;
public static void main(String []args){int []arr = {9,8,7,6,5,4,3,2,1};n = arr.length;sort(arr);System.out.println(Arrays.toString(arr));
}// init
public static void sort(int []arr) {// 1.构建大顶堆// 从第一个非叶子结点从下至上，从右至左(从下至上)调整结构for (int i = n / 2 - 1; i >= 0; i--) {adjustHeap(arr, i, n);}// 2.调整堆结构+交换堆顶元素与末尾元素for (int j = n - 1; j > 0; j--) {out(arr[0]);swap(arr, 0, j); //将堆顶元素与末尾元素进行交换adjustHeap(arr, 0, j);//重新对堆进行调整}
}// 调整大顶堆（仅是调整过程，建立在大顶堆已构建的基础上）
public static void adjustHeap(int []arr, int i, int length) {int temp = arr[i];//先取出当前元素ifor(int k = i*2+1; k < length; k = k*2+1) { //从i结点的左子结点开始，也就是2i+1处开始if (k + 1 < length && arr[k] < arr[k+1]) {//左子结点小于右子结点，k指向右子结点k++;}if (arr[k] > temp) {//如果子节点大于父节点，将子节点值赋给父节点（不用进行交换）arr[i] = arr[k];i = k;} else {break;}}arr[i] = temp;//将temp值放到最终的位置
}// 交换元素
public static void swap(int []arr,int a ,int b){int temp=arr[a];arr[a] = arr[b];arr[b] = temp;
}

最大最小堆动态过程

class myHeap {int idx = 0;//idx也是sizeint maxLen = 100;//默认100int [] heap;public myHeap(){heap = new int[maxLen];}public myHeap(int len){maxLen = len;heap = new int[maxLen];}public void push(int v){if (idx >= maxLen) return;int i = idx++;//得到自己的idxwhile (i > 0){int p = (i-1)/2;//p是父亲if (heap[p] <= v)//最小根 已经结束break;heap[i] = heap[p];i = p;}heap[i] = v;}public int pop(){//提取并删除最小值// 最小值int res = heap[0];int v = heap[--idx];heap[idx] = 0;//把要提上去的数值清零 此处已不存放数int i = 0;//i是v要存放的位置int k = 1;//i*2 + 1while (k < idx){if (k+1 < idx && heap[k+1] < heap[k]) k = k + 1;if (heap[k] >= v) break;heap[i] = heap[k];i = k;k = k*2+1;}heap[i] = v;return res;}
}

6.桶排序

乍一看和归并很像，其实不一样，最大的区别是桶排序的每个桶之间是有序的，如A桶的最大值小于B组的最小值。

桶排序通常是一中非常高效的排序算法，它通过空间换取时间，可以做到线性时间复杂度，具体算法介绍如下：

1. 在已知数据的范围的条件下，通过将数据装入对应范围的桶中,(桶内如插入排序 On)，最后扫描桶来实现排序。显然，这个算法应用的前提是需要知道所排序数据的范围，或者求出。

2. 桶排序举例

（1）对1万学生的数学成绩进行排序

假设对1万学生的数学成绩进行排序，分数默认为（0-100，假设为整数），应用桶排序的过程如下：

首先，建立101个桶，用数组a[0...100]表示，一次扫描1万条数据，根据每条数据的值，记录到对应下标的桶中。比如，小明的分数是90，则a[90]加一；然后扫描这101个桶，即可得到有序数组。如：

一个简单的示例：所有的数据都在0-5范围内：

4，5，2，3，1，4，3，2，1，5，2，2，4，5，1，3，4，1，3，2，2

排序后.....

1，1，1，1，2，2，2，2，2，2，3，3，3，3，4，4，4，4，5，5，5

（2）将20个范围为0-999的整数进行排序

如果按照1中的思路，则需要创建999个桶，然后进行一趟桶排序即可。

但是还有另外一种方式，只创建10个桶，但是要进行3趟桶排序。

10个桶对应0-9 一共10个不同的数字，说白了就是一个长度为10的整型数组。3趟桶排序是因为：0-999范围内的数由3个位组成：个位、十位、百位

（这里写反了吧，可以先对百位数排序一遍，再对十位数，再对个位数，高阶位不足的用0代替、放入0桶）

第一趟对个位数进行桶排序，根据个位数的值，将该数放入对应的桶中，比如425，个位数为5，则将425放到a[5]中---（这是将元素本身放到桶中，不是计数，这种方式待排序的元素个数不能超过桶的个数！！！）

第二趟对十位数进行桶排序，根据十位数.....

第三趟对百位数进行桶排序，根据百位数.....

具体的实现可以这样：

在第一趟桶排序时，将待排的20个数依次放到桶中。然后，再把这20个数拷贝回原数组，然后再根据十位数排序:根据十位数的大小将这20个数按顺序放到桶中，然后再把十位数有序的桶中的数据复制回原数组......百位数....

最终，原数组中的数据就是已经排好序的数据了。

3. 桶排序时间复杂度分析

（桶排序可以做到线性时间复杂度，比如上面的1万名学生的成绩排序。将1万条成绩数据输入，复杂度是O(N)，输出排序结果时遍历每个桶复杂度是O(M)，故总时间复杂度是O(M+N)。而这种情况下桶的个数远远小于数据条数。

对于使用多趟桶排序的情形，时间复杂度是O(p(N+b))，其中N是输入的数的据量，b是桶的个数，p是桶排序趟数。）

假设有n个数字，有m个桶，如果数字是平均分布的，则每个桶里面平均有n/m个数字。如果对每个桶中的数字采用快速排序，那么整个算法的复杂度是：O(n + m * n/m*log(n/m)) = O(n + nlogn – nlogm)

从上式看出，当m接近n的时候，桶排序复杂度接近O(n)

当然，以上复杂度的计算是基于输入的n个数字是平均分布这个假设的。这个假设是很强的，实际应用中效果并没有这么好。如果所有的数字都落在同一个桶中，那就退化成一般的排序了。

排序算法的时间复杂度都是O（n^2），也有部分排序算法时间复杂度是O(nlogn)。而桶式排序却能实现O（n）的时间复杂度。但桶排序的缺点是：

1）首先是空间复杂度比较高，需要的额外开销大。排序有两个数组的空间开销，一个存放待排序数组，一个就是所谓的桶，比如待排序值是从0到m-1，那就需要m个桶，这个桶数组就要至少m个空间。

2）其次待排序的元素都要在一定的范围内等等。

代码：

/****************************************************************************  @file       main.cpp*  @author     MISAYAONE*  @date       27  March 2017*  @remark     27  March 2017 *  @theme      Bucket Sort ***************************************************************************/#include <iostream>
#include <vector>
#include <time.h>
#include <Windows.h>
using namespace std;void Bucket_sort(double a[],size_t n)
{double **p = new double *[10];//p数组存放十个double指针，分为10个桶for (int i=0; i < 10; ++i){p[i] = new double[100];//每个指针都指向一块10个double的数组，每个桶都可以包含100个元素}int count[10] = {0};//元素全为0的数组for (int i = 0; i < n; ++i){double temp = a[i];int flag = (int)(temp*10);//判断每个元素属于哪个桶p[flag][count[flag]] = temp;//将每个元素放入到对应的桶中，从0开始int j = count[flag]++;//将对应桶的计数加1//在本桶之中与之前的元素做比较，比较替换（插入排序）for (;j > 0 && temp < p[flag][j-1];--j){p[flag][j] = p[flag][j-1];}p[flag][j] = temp;}//元素全部放完之后，需要进行重新链接的过程int k = 0;for (int i = 0; i < 10; ++i){for (int j = 0; j < count[i]; ++j)//桶中元素的个数count[i]{a[k++] = p[i][j];}}//申请内存的释放for (int i = 0 ; i<10 ;i++)  {  delete p[i];  p[i] =NULL;  }  delete []p;  p = NULL;  
}  void Bucket_sort(vector<double>::iterator begin,vector<double>::iterator end)
{double **p = new double*[10];//分10个桶for (int i = 0; i < 10; ++i){p[i] = new double[end-begin];//每个桶至多存放end-begin个元素}auto iter1 = begin;int count[10] = {0};//桶内元素计数for (iter1; iter1 != end; ++iter1){double temp = *iter1;//保存当前值int flag = (int)(temp*10);//确定桶序号p[flag][count[flag]] = temp;int j = count[flag]++;//桶内元素计数加一for (j;j >0 && temp < p[flag][j-1]; --j){p[flag][j] = p[flag][j-1];}p[flag][j] = temp;//将本值插入桶中的适当位置}for (int i = 0; i < 10; ++i){for (int j = 0; j < count[i]; ++j){*begin++ = p[i][j];}}for (int i = 0; i < 10; ++i){delete p[i];p[i] = NULL;}delete []p;p = NULL;
}//随机初始化数组[0,1)
void Initial_array(double a[],size_t n)
{for (size_t i = 0; i < n; ++i){//rand()的返回值应该是[0, RAND_MAX]，最小可能为0，最大可能为RAND_MAX。//rand()/(RAND_MAX+0.0)和rand()/(RAND_MAX+1.0)//当rand()返回0，前者为0，后者为0//当rand()返回RAND_MAX，前者为1，后者为非常接近1的一个小数。a[i] = rand()/double(RAND_MAX+1);}
}int main(int argc, char **argv)
{double a[50];Initial_array(a,50);vector<double> vec(a,a+50);Bucket_sort(a,50);for (int i = 0; i < 50; ++i){cout<<a[i]<<" ";}cout<<endl;Bucket_sort(vec.begin(),vec.end());for (int i = 0; i < 50; ++i){cout<<vec[i]<<" ";}cin.get();return 0;
}

下面是例题：

例题1：一年的全国高考考生人数为500 万，分数使用标准分，最低100 ，最高900 ，没有小数，你把这500 万元素的数组排个序。
对500W数据排序，如果基于比较的先进排序，平均比较次数为O(5000000*log5000000)≈1.112亿。但是我们发现，这些数据都有特殊的条件： 100=<score<=900。那么我们就可以考虑桶排序这样一个“投机取巧”的办法、让其在毫秒级别就完成500万排序。
创建801(900-100)个桶。将每个考生的分数丢进f(score)=score-100的桶中。这个过程从头到尾遍历一遍数据只需要500W次。然后根据桶号大小依次将桶中数值输出，即可以得到一个有序的序列。而且可以很容易的得到100分有***人，501分有***人。
实际上，桶排序对数据的条件有特殊要求，如果上面的分数不是从100-900，而是从0-2亿，那么分配2亿个桶显然是不可能的。所以桶排序有其局限性，适合元素值集合并不大的情况。

例题2：在一个文件中有 10G 个整数，乱序排列，要求找出中位数。内存限制为 2G。只写出思路即可（内存限制为 2G的意思就是，可以使用2G的空间来运行程序，而不考虑这台机器上的其他软件的占用内存）。

分析：既然要找中位数，很简单就是排序的想法。那么基于字节的桶排序是一个可行的方法。
思想：将整型的每1byte作为一个关键字，也就是说一个整形可以拆成4个keys，而且最高位的keys越大，整数越大。如果高位keys相同，则比较次高位的keys。整个比较过程类似于字符串的字典序。按以下步骤实施：
1、把10G整数每2G读入一次内存，然后一次遍历这536,870,912即（1024*1024*1024）*2 /4个数据。每个数据用位运算">>"取出最高8位(31-24)。这8bits(0-255)最多表示255个桶，那么可以根据8bit的值来确定丢入第几个桶。最后把每个桶写入一个磁盘文件中，同时在内存中统计每个桶内数据的数量，自然这个数量只需要255个整形空间即可。
2、继续以内存中的整数的次高8bit进行桶排序(23-16)。过程和第一步相同，也是255个桶。
3、一直下去，直到最低字节(7-0bit)的桶排序结束。我相信这个时候完全可以在内存中使用一次快排就可以了。

例题3：给定n个实数x1,x2,...,xn,求这n个实数在实轴上相邻2个数之间的最大差值M,要求设计线性的时间算法
典型的最大间隙问题。

要求线性时间算法。需要使用桶排序。桶排序的平均时间复发度是O(N).如果桶排序的数据分布不均匀，假设都分配到同一个桶中，最坏情况下的时间复杂度将变为O(N^2).
桶排序: 最关键的建桶，如果桶设计得不好的话桶排序是几乎没有作用的。通常情况下，上下界有两种取法，第一种是取一个10^n或者是2^n的数，方便实现。另一种是取数列的最大值和最小值然后均分作桶。对于这个题，最关键的一步是：由抽屉原理知：最大差值M>= (Max(V[n])-Min(V[n]))/(n-1)！所以，假如以

(Max(V[n])-Min(V[n]))/(n-1)为桶宽的话，答案一定不是属于同一个桶的两元素之差。因此，这样建桶，每次只保留桶里面的最大值和最小值即可。

leetcode例题：347. 前 K 个高频元素

    //347. 前 K 个高频元素 桶排序简单例题public int[] topKFrequent(int[] nums, int k) {Map<Integer,Integer> map = new HashMap<>();for(int n : nums) map.put(n,map.getOrDefault(n,0)+1);List<Integer> [] buckets = new List[nums.length+1];//将频率作为数组下标，对于出现频率不同的数字集合，存入对应的数组下标for(int key : map.keySet()){int v = map.get(key);if(buckets[v] == null) buckets[v] = new ArrayList<>();buckets[v].add(key);}List<Integer> res = new ArrayList<>();for(int i = buckets.length - 1;i >= 0 && res.size()<k;i--){if(buckets[i]!=null) res.addAll(buckets[i]);}return res.stream().mapToInt(Integer::valueOf).toArray();}

7.topk解法

问题描述：

从arr[1, n]这n个数中，找出最大的k个数，这就是经典的TopK问题。

栗子：

从arr[1, 12]={5,3,7,1,8,2,9,4,7,2,6,6} 这n=12个数中，找出最大的k=5个。

（桶排序也能解决topk问题）

一、排序

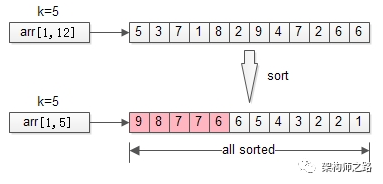
排序是最容易想到的方法，将n个数排序之后，取出最大的k个，即为所得。

伪代码：

sort(arr, 1, n);

return arr[1, k];

时间复杂度：O(n*lg(n))

分析：明明只需要TopK，却将全局都排序了，这也是这个方法复杂度非常高的原因。那能不能不全局排序，而只局部排序呢？这就引出了第二个优化方法。

二、局部排序

不再全局排序，只对最大的k个排序。

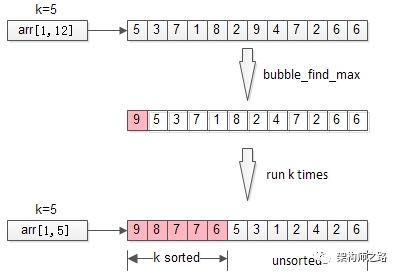
冒泡是一个很常见的排序方法，每冒一个泡，找出最大值，冒k个泡，就得到TopK

伪代码：

for(i=1 to k){

bubble_find_max(arr,i);

}

return arr[1, k];

时间复杂度：O(n*k)

分析：冒泡，将全局排序优化为了局部排序，非TopK的元素是不需要排序的，节省了计算资源。不少朋友会想到，需求是TopK，是不是这最大的k个元素也不需要排序呢？这就引出了第三个优化方法。

三、堆

思路：只找到TopK，不排序TopK。

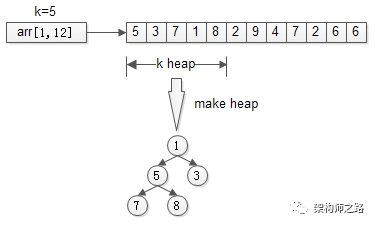
先用前k个元素生成一个小顶堆，这个小顶堆用于存储，当前最大的k个元素。(因为要与k个数中最小的数比较)

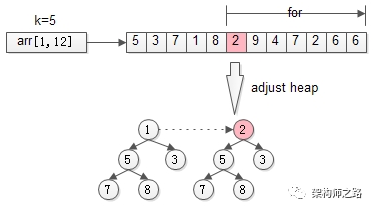
接着，从第k+1个元素开始扫描，和堆顶（堆中最小的元素）比较，如果被扫描的元素大于堆顶，则替换堆顶的元素，并调整堆，以保证堆内的k个元素，总是当前最大的k个元素。

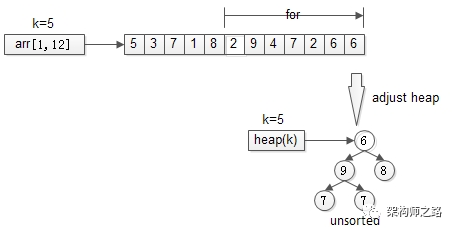
直到，扫描完所有n-k个元素，最终堆中的k个元素，就是猥琐求的TopK。

伪代码：

heap[k] = make_heap(arr[1, k]);

for(i=k+1 to n){

adjust_heap(heep[k],arr[i]);

}

return heap[k];

时间复杂度：O(n*lg(k))

画外音：n个元素扫一遍，假设运气很差，每次都入堆调整，调整时间复杂度为堆的高度，即lg(k)，故整体时间复杂度是n*lg(k)。

分析：堆，将冒泡的TopK排序优化为了TopK不排序，节省了计算资源。堆，是求TopK的经典算法，那还有没有更快的方案呢？

四、随机选择

随机选择算在是《算法导论》中一个经典的算法，其时间复杂度为O(n)，是一个线性复杂度的方法。

前序知识，一个所有程序员都应该烂熟于胸的经典算法：快速排序。

其伪代码是：

void quick_sort(int[]arr, int low, inthigh){

         if(low== high) return;

         int i = partition(arr, low, high);

         quick_sort(arr, low, i-1);

         quick_sort(arr, i+1, high);

}

其核心算法思想是，分治法。

分治法（Divide&Conquer），把一个大的问题，转化为若干个子问题（Divide），每个子问题“都”解决，大的问题便随之解决（Conquer）。这里的关键词是“都”。从伪代码里可以看到，快速排序递归时，先通过partition把数组分隔为两个部分，两个部分“都”要再次递归。

分治法有一个特例，叫减治法。

减治法（Reduce&Conquer），把一个大的问题，转化为若干个子问题（Reduce），这些子问题中“只”解决一个，大的问题便随之解决（Conquer）。这里的关键词是“只”。

二分查找binary_search，BS，是一个典型的运用减治法思想的算法，其伪代码是：

int BS(int[]arr, int low, inthigh, int target){

         if(low> high) return -1;

         mid= (low+high)/2;

         if(arr[mid]== target) return mid;

         if(arr[mid]> target)

                   return BS(arr, low, mid-1, target);

         else

                   return BS(arr, mid+1, high, target);

}

从伪代码可以看到，二分查找，一个大的问题，可以用一个mid元素，分成左半区，右半区两个子问题。而左右两个子问题，只需要解决其中一个，递归一次，就能够解决二分查找全局的问题。

通过分治法与减治法的描述，可以发现，分治法的复杂度一般来说是大于减治法的：

快速排序：O(n*lg(n))

二分查找：O(lg(n))

话题收回来，快速排序的核心是：

i = partition(arr, low, high);

这个partition是干嘛的呢？

顾名思义，partition会把整体分为两个部分。

更具体的，会用数组arr中的一个元素（默认是第一个元素t=arr[low]）为划分依据，将数据arr[low, high]划分成左右两个子数组：

左半部分，都比t大
右半部分，都比t小
中间位置i是划分元素

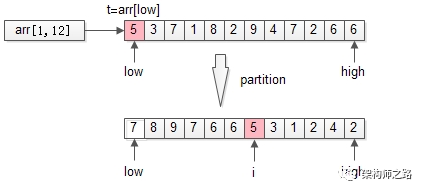
以上述TopK的数组为例，先用第一个元素t=arr[low]为划分依据，扫描一遍数组，把数组分成了两个半区：

左半区比t大
右半区比t小
中间是t

partition返回的是t最终的位置i。

很容易知道，partition的时间复杂度是O(n)。

画外音：把整个数组扫一遍，比t大的放左边，比t小的放右边，最后t放在中间N[i]。

partition和TopK问题有什么关系呢？

TopK是希望求出arr[1,n]中最大的k个数，那如果找到了第k大的数，做一次partition，不就一次性找到最大的k个数了么？

画外音：即partition后左半区的k个数。

问题变成了arr[1, n]中找到第k大的数。

再回过头来看看第一次partition，划分之后：

i = partition(arr, 1, n);

如果i大于k，则说明arr[i]左边的元素都大于k，于是只递归arr[1, i-1]里第k大的元素即可；

如果i小于k，则说明说明第k大的元素在arr[i]的右边，于是只递归arr[i+1, n]里第k-i大的元素即可；

画外音：这一段非常重要，多读几遍。

这就是随机选择算法randomized_select，RS，其伪代码如下：

int RS(arr, low, high, k){

if(low== high) return arr[low];

i= partition(arr, low, high);

temp= i-low; //数组前半部分元素个数

if(temp>=k)

return RS(arr, low, i-1, k); //求前半部分第k大

else

return RS(arr, i+1, high, k-i); //求后半部分第k-i大

}

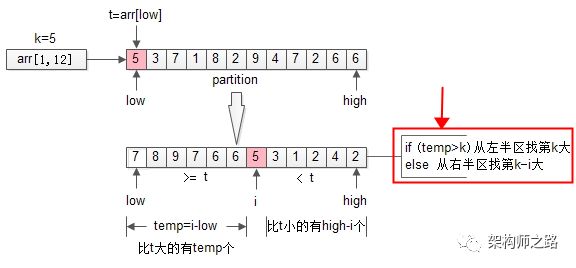
这是一个典型的减治算法，递归内的两个分支，最终只会执行一个，它的时间复杂度是O(n)。

再次强调一下：

分治法，大问题分解为小问题，小问题都要递归各个分支，例如：快速排序
减治法，大问题分解为小问题，小问题只要递归一个分支，例如：二分查找，随机选择

通过随机选择（randomized_select），找到arr[1, n]中第k大的数，再进行一次partition，就能得到TopK的结果。

例题：973. 最接近原点的 K 个点

inline int distToOrigin(vector<int> &p)
{return p[0] * p[0] + p[1] * p[1];}
class Solution {
public://快排思想void partion(vector<vector<int>>& points, int k,int left,int right){if(left==k) return;int l = left,r = right;vector<int> idx = points[left];int pv_idx = distToOrigin(idx);while(l<r){while(l<r && distToOrigin(points[r]) >= pv_idx) r--;points[l] = points[r];while(l<r && distToOrigin(points[l]) <= pv_idx) l++;points[r] = points[l];}points[l] = idx;if(l+1==k) return;else if(l+1<k) partion(points,k,l+1,right);else partion(points,k,left,l-1);}vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {partion(points,k,0,points.size()-1);return vector<vector<int>>(points.begin(),points.begin()+k);}
};

五、总结

TopK，不难；其思路优化过程，不简单：