0. Tips

1. 位运算

如何枚举一个二进制状态数字k的子集, 方法就是针对中的二进制为1的位开始进行减法，判断数字k的二进制子集, 像枚举(2^k-1) ~ 0一样枚举其子集；

    int sub = k;do {sub = (sub - 1) & k;} while(sub != k);

比如k = 10101的二进制子集有:
10101
10100
10001
10000
00101
00100
00001
00000

00000再-1为11111，&k后就等于k；

求1的个数
#include <cstdio>
int main(){int n, cnt;cnt = 0;scanf("%d", &n);while (n) {cnt += (n & 1);n >>= 1;}printf("%d\n", cnt);
}或者
int BitCount(unsigned int n)
{unsigned int c =0 ;for (c =0; n; ++c){n &= (n -1) ; // 清除最低位的1}return c ;
}

2. 快速幂

算法学习笔记(4)：快速幂 - 知乎

//递归快速幂
int qpow(int a, int n)
{if (n == 0)return 1;else if (n % 2 == 1)return qpow(a, n - 1) * a;else{int temp = qpow(a, n / 2);return temp * temp;}
}//递归快速幂（对大素数取模）
#define MOD 1000000007
typedef long long ll;
ll qpow(ll a, ll n)
{if (n == 0)return 1;else if (n % 2 == 1)return qpow(a, n - 1) * a % MOD;else{ll temp = qpow(a, n / 2) % MOD;return temp * temp % MOD;}
}//非递归快速幂
int qpow(int a, int n){int ans = 1;while(n){if(n&1)        //如果n的当前末位为1ans *= a;  //ans乘上当前的aa *= a;        //a自乘n >>= 1;       //n往右移一位}return ans;
}
//泛型的非递归快速幂
template <typename T>
T qpow(T a, ll n)
{T ans = 1; // 赋值为乘法单位元，可能要根据构造函数修改while (n){if (n & 1)ans = ans * a; // 这里就最好别用自乘了，不然重载完*还要重载*=，有点麻烦。n >>= 1;a = a * a;}return ans;
}

3. 字符串

匹配算法1

Rabin-Karp算法

Rabin-Karp算法：寻找字符串S中字符串T出现的位置或次数的问题属于字符串匹配问题

Rabin–Karp 把字符串转化为一个hash值 不断滑动窗口进出的思想，如何构造这一个hash值？

1044. 最长重复子串

    // 1044. 最长重复子串// 二分法 + 字符串匹配算法 -- Rabin–Karp 把字符串转化为一个hash值 不断滑动窗口// 子串长度[0,n) 在这个范围内枚举当前值mid 若存在mid长的重复子串 则更新l=mid+1 否则r=mid-1// https://www.cnblogs.com/grandyang/p/14497723.htmlstring longestDupSubstring(string S) {int n = S.size();int l = 0, r = n, mod = 1e7 + 7;string res;// power 记录每个位置的阶数vector<int> power(n,1);for (int i = 1; i < n; i++) {power[i] = (power[i-1]*26) % mod;}while (l < r) {int mid = l + (r-l)/2;// rabinKarp 检查是否存在长度为mid的重复子串string cur = rabinKarp(mid, S, power);if (cur.size() > res.size()) {res = cur;l = mid + 1;} else {// 注意二分的边界 r取不到,所以r=midr = mid;}}return res;}string rabinKarp(int len, string s, vector<int> power) {if (len == 0) return "";unordered_map<int, vector<int>> hash;int cur = 0, mod = 1e7 + 7;for (int i = 0; i < len; ++i) {cur = (cur * 26 + s[i]-'a') % mod;}hash[cur] = {0};for (int i = len; i < s.size(); ++i) {// 此处不加mod的话，%后可能小于modcur = ((cur - (s[i-len]-'a') * power[len-1]) % mod + mod) % mod;cur = (cur * 26 + (s[i]-'a')) % mod;if (hash.count(cur)) {for (int t : hash[cur]) {if (s.substr(i - len + 1, len) == s.substr(t, len)) {return s.substr(t, len);}}hash[cur].push_back(i - len + 1);} else {hash[cur] = {i- len + 1};}}return "";}

GO SDK库的RK算法： 

// PrimeRK is the prime base used in Rabin-Karp algorithm.
const PrimeRK = 16777619func HashStr(sep string) (uint32, uint32) {hash := uint32(0)for i := 0; i < len(sep); i++ {hash = hash*PrimeRK + uint32(sep[i])}var pow, sq uint32 = 1, PrimeRKfor i := len(sep); i > 0; i >>= 1 {if i&1 != 0 {pow *= sq}sq *= sq}return hash, pow
}func IndexRabinKarp(s, substr string) int {// Rabin-Karp searchhashss, pow := HashStr(substr)n := len(substr)var h uint32for i := 0; i < n; i++ {h = h*PrimeRK + uint32(s[i])}if h == hashss && s[:n] == substr {return 0}for i := n; i < len(s); {h *= PrimeRKh += uint32(s[i])h -= pow * uint32(s[i-n])i++if h == hashss && s[i-n:i] == substr {return i - n}}return -1
}

匹配算法2

KMP算法

彻底理解KMP_CSDN

1.字典树

字典树，又称 Trie 树，是一种树形结构。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串）。主要思想是利用字符串的公共前缀来节约存储空间。 

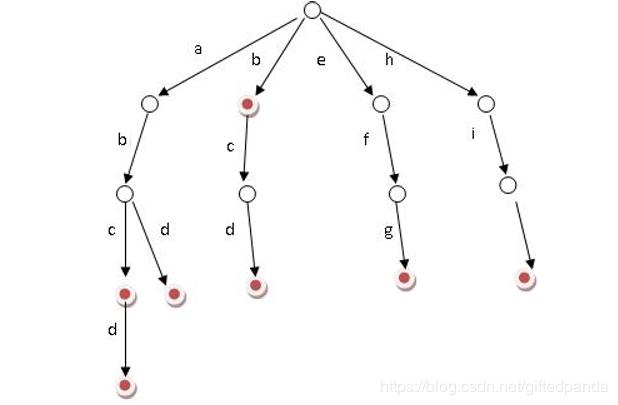
在实际运用中，比如我们要储存大量的单词在一个文本中，而且还要查找某个单词是否存在，如果存在，请输出出现了多少次。考虑到有大量的单词而且还要询问出现了多少次，考虑到无法用字符串直接存储并进行遍历，所以就有了字典树这种高级数据结构。字典树的主要思想是利用字符串的公共前缀来节约存储空间。

如上图所示，从根节点开始到每一个红色标记(end)的结点都是一个单词，上图中储存的字符串有"abc"、"abcd" 、"abd" 、"b"、"bcd"、"efg"、"hi"。当有大量单词是就可以利用字典树这种高级数据结构就可以节约存储空间。

字典树的实现方式有两种，1：通过结构体指针来实现，2：通过数组来实现

两种实现方式主要区别在于，数组实现的字典树比结构体指针实现的字典更节省内存，只要不是特别卡内存，建议用结构体指针实现，比较好写也易于理解，下面详细讲解一下字典树的结构体实现，以leetcode 472题为例

    static class TrieNode {TrieNode[] children;boolean isWord;//还可以在这里记录终止于此的单词个数 int numpublic TrieNode() {children = new TrieNode[26];}}private TrieNode trie_root;public List<String> findAllConcatenatedWordsInADict_(String[] words){List<String> res = new ArrayList<>();trie_root = new TrieNode();//初始化字典树for (String w:words) {TrieNode cur = trie_root;for(char c : w.toCharArray()){if(cur.children[c-'a']==null) cur.children[c-'a'] = new TrieNode();cur = cur.children[c-'a'];}cur.isWord = true;//cur.num++;}for (String w:words){if(find_word(w,0,0,trie_root)) res.add(w);}return res;}public boolean find_word(String word,int depth,int idx,TrieNode node){if(idx == word.length() && depth>1) return true;//记录深度 避免是自己for (int i = idx; i < word.length(); i++) {//迭代查找树node = node.children[word.charAt(i)-'a'];if(node == null) return false;//end 开启新一轮递归if (node.isWord && find_word(word,depth+1,i+1,trie_root)) return true;}return false;}

677. 键值映射

class MapSum {/* 1. 使用HashMap结构Map <String,Integer>map = new HashMap<>();public MapSum() {}public void insert(String key, int val) {map.put(key,val);}public int sum(String prefix) {int res = 0;for (var t:map.entrySet()) {String key = t.getKey();if(key.indexOf(prefix)==0) res += t.getValue();}return res;}*///2. 自己构造字典前缀树private class TrieNode{private int val;private TrieNode[] next;public TrieNode(){//this.val = val;next = new TrieNode[26];}}TrieNode root;public MapSum() {root = new TrieNode();}public void insert(String key, int val) {TrieNode cur = root;for (char c : key.toCharArray()){if(cur.next[c-'a']==null) cur.next[c-'a'] = new TrieNode();cur = cur.next[c-'a'];}cur.val = val;}public int sum(String prefix) {TrieNode cur = root;for (char c : prefix.toCharArray()){if(cur.next[c-'a']==null) return 0;cur = cur.next[c-'a'];}return getSum(cur);//前缀到此为止 下面用递归，迭代解决不了}public int getSum(TrieNode pre){//寻找后续的所有树枝int res = pre.val;for (TrieNode child : pre.next) {//遍历所有可能的子树if(child!=null) res += getSum(child);}return res;}
}

212. 单词搜索 II

class Solution {Set<String> res = new HashSet<String>();int[][] dir = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};public List<String> findWords(char[][] board, String[] words) {Trie root = new Trie();for (String word : words){root.insert(word);}for (int i = 0; i < board.length; ++i) {for (int j = 0; j < board[0].length; ++j){if (root.child[board[i][j]-'a'] != null){dfs(board, i, j, root);}}}return new ArrayList<String>(res);}public void dfs(char[][] board, int i, int j, Trie cur){char c = board[i][j];if (c == '.') return;if (cur.child[c-'a']==null) return;cur = cur.child[c - 'a'];//System.out.println(cur.word);if (cur.end){res.add(cur.word);//return; 继续搜索 bad case：oa oaa}board[i][j] = '.';for (int[] d: dir){int i2 = i + d[0], j2 = j + d[1];if (i2 >= 0 && i2 < board.length && j2 >= 0 && j2 < board[0].length) {dfs(board, i2, j2, cur);}}board[i][j] = c;}
}
class Trie{Trie[] child;boolean end = false;String word;public Trie(){word = "";child = new Trie[26];}public void insert(String word){Trie cur = this;//注意这种写法char [] chs = word.toCharArray();for (char c : chs){if(cur.child[c-'a']==null) cur.child[c-'a'] = new Trie();cur = cur.child[c-'a'];}cur.end = true;cur.word = word;}
}

2.并查集

并查集主要用于解决一些元素分组的问题。它管理一系列不相交的集合，并支持两种操作：

• 合并（Union）：把两个不相交的集合合并为一个集合。
• 查询（Find）：查询两个元素是否在同一个集合中。

先初始化

int fa[MAXN];
inline void init(int n)
{for (int i = 1; i <= n; ++i)fa[i] = i;
}

遍历查询 + 合并

//未压缩路径
int find(int x)
{if(fa[x] == x)return x;elsereturn find(fa[x]);
}

inline void merge(int i, int j)
{fa[find(i)] = find(j);
}

以leetcode 990. 等式方程的可满足性 为例

class Solution {int [] parent = new int[26];private void union(int a,int b){parent[find(a)] = find(b); }private int find(int x){if(x!=parent[x])parent[x] = find(parent[x]);return parent[x];}public boolean equationsPossible(String[] equations) {for(int i = 0;i<26;i++)parent[i] = i;for(String str : equations){if(str.charAt(1) == '=')union(str.charAt(0) - 'a',str.charAt(3) - 'a');}for(String str : equations){if(str.charAt(1) == '!' && find(str.charAt(0) - 'a') == find(str.charAt(3) - 'a'))return false;}return true;}
}

上面已经进行过路径压缩 

LeetCode 721. 账户合并

class Solution {//721. 账户合并 并查集class DSU{//放到class里int [] parent;public DSU(int n){parent = new int[n];for (int i = 0;i<n;i++)parent[i] = i;}public int find(int x){if(parent[x] != x)parent[x] = find(parent[x]);return parent[x];}public void union(int x,int y){parent[find(x)] = find(y);}}public List<List<String>> accountsMerge(List<List<String>> accounts) {HashMap<String,Integer> email_id = new HashMap<>();//记录每个邮箱地址的主人HashMap<String,String> email_name = new HashMap<>();//记录邮箱地址的id 后面进行同类邮箱地址合并DSU dsu = new DSU(10001);//邮箱地址的最大数量int id = 0;for (var account:accounts) {String name = "";for(String email : account){if(name==""){name = account.get(0);continue;}email_name.put(email,name);if(!email_id.containsKey(email)){email_id.put(email,id++);}dsu.union(email_id.get(account.get(1)),email_id.get(email));}}Map<Integer,List<String>> res = new HashMap<>();for(String email : email_id.keySet()){//同类邮箱地址整合int idx = dsu.find(email_id.get(email));res.computeIfAbsent(idx,a->new ArrayList()).add(email);}for(var list : res.values()){//添加名字Collections.sort(list);list.add(0,email_name.get(list.get(0)));}return new ArrayList<>(res.values());}
}

947. 移除最多的同行或同列石头  “二维”并查集 每个元素有两个属性；

    //二维并查集int parent[] = new int[20002];public int find(int x){if (parent[x] != x) parent[x] = find(parent[x]);return parent[x];}// 可以看成将x->y 这条边加入并查集 以y为代表public void union(int x,int y){//parent[find(x)] = find(y);int px = find(x);int py = find(y);if (px == py) return;parent[px] = py;}//思路是要先把每个石头的两个坐标元素整合为一个集合public int removeStones(int[][] stones) {int base = 10001;for (int[] st : stones) {parent[st[0]] = st[0];parent[st[1]+base] = st[1]+base;}//把x值相同的root即y去指向同一root 还要注意上面是怎么union的//举例(1,10);(2,10);(1,9);显然 set里会把前两个去掉；//第三个的话 1先指向10 union时再把1和10一起指向9；set.addd(find)时就去重了 要理解union本质for (int[] st : stones) union(st[0],st[1]+base);Set<Integer> set = new HashSet<>();for (int[] st : stones){set.add(find(st[1]+base));}return stones.length - set.size();}

3.单调栈

 单调栈就是栈里面存放的数据都是有序的,所以可以分为单调递增栈和单调递减栈两种。

402. 移掉K位数字

   //单调栈  从前到后遍历 高位删除较大的数public String removeKdigits(String num, int k) {if(num.length()==k) return "0";Deque<Character> deque = new LinkedList<>();for (char c:num.toCharArray()) {while (!deque.isEmpty() && deque.peekLast() > c && k >0){deque.pollLast();k--;}deque.offerLast(c);}while (k-- > 0) deque.pollLast();StringBuilder res = new StringBuilder();boolean frontZero = true;for (char c : deque){if (frontZero && c=='0') continue;frontZero = false;res.append(c);}return res.length()==0 ? "0" : res.toString();//避免删除后全是0的情况}

316. 去除重复字母

class Solution {//316. 去除重复字母 与1081 same.  like 321,402//azad zazd//压栈 类似单调栈 当栈顶大于当前的c且栈顶可以被替换(即后续的s中有栈顶元素) 删除栈顶public String removeDuplicateLetters(String s) {Stack<Character> stack = new Stack<>();for (int i = 0;i<s.length();i++) {char c = s.charAt(i);if (stack.contains(c)) continue;while (!stack.isEmpty() && stack.peek() > c && s.indexOf(stack.peek(),i)!=-1)stack.pop();stack.push(c);}StringBuilder sb = new StringBuilder();for (char c : stack) sb.append(c);return sb.toString();}
}

321. 拼接最大数

    //321. 拼接最大数  思路：最终的数组两部分来源于s1和s2，而且这两部分分别是各自s1和s2的最大值//两部分的长度和为k  遍历取最大值即可public int[] maxNumber(int[] nums1, int[] nums2, int k) {int[] res = new int[k];int maxI = Math.min(nums1.length,k);for (int i = Math.max(k-nums2.length,0); i <= maxI; i++) {//i表示s1的长度  k-i是s2的长度int[] cur = mergeArray(getMaxArray(nums1,i),getMaxArray(nums2,k-i));if(compareArray(cur,0,res,0)) res = cur;}return res;}//合并数组  不能按归并那样合并 如[7,6] [7,8] 可能产生 7 7 8 6；实际是7876public int[] mergeArray(int[] nums1, int[] nums2){int [] res = new int[nums1.length + nums2.length];int cur = 0, p1 = 0, p2 = 0;while (cur < nums1.length + nums2.length){if (compareArray(nums1, p1, nums2, p2))//如果当前值相等还需要比较后续哪个大res[cur++] = nums1[p1++];elseres[cur++] = nums2[p2++];}return res;}//获取长度为k的最大子序列   类似于单调栈public int[] getMaxArray(int[] nums,int k){int[] res = new int[k];int n = nums.length;int pop_cnt = n - k;//表示最多弹出的数量 再多弹的话凑不够k个数了int cur = 0;//cur-1表示栈顶，cur表示即将添加元素的位置for (int i = 0; i < n; i++) {while(cur>0 && res[cur-1] < nums[i] && pop_cnt>0){cur--;pop_cnt--;}if (cur<k) res[cur++] = nums[i];else pop_cnt--;//注意这里 要-- 不然pop_cnt偏大 会多弹导致不够k个}return res;}public boolean compareArray(int[] nums1, int p1, int[] nums2, int p2) {if (p2 >= nums2.length) return true;if (p1 >= nums1.length) return false;if (nums1[p1] > nums2[p2]) return true;if (nums1[p1] < nums2[p2]) return false;return compareArray(nums1, p1 + 1, nums2, p2 + 1);}

题外话：在遍历数组时，如果想获得比当前小的最大值，由后向前遍历；最小值，从前向后；

738. 单调递增的数字

    //倒序扫描数字，若当前数字比其右边一位大，则把该位数字减1，最后将flag右边的所有位改成9public int monotoneIncreasingDigits(int N) {if (N<10) return N;StringBuilder sb = new StringBuilder(String.valueOf(N));int flag = -1;//记录for (int i = sb.length()-2;i>=0;i--){//倒着 因为-1后可能左边又大于此处了if (sb.charAt(i)>sb.charAt(i+1)){sb.setCharAt(i,(char)(sb.charAt(i)-1));flag = i;/*while (++i< sb.length()){sb.setCharAt(i,'9');}*/}}if (flag==-1) return N;while (++flag < sb.length()) sb.setCharAt(flag,'9');return Integer.valueOf(sb.toString());}

4. 二分

二分思路梳理

34. 在排序数组中查找元素的第一个和最后一个位置 下面是二分的两种写法，第一种是未确定有序数组中是否含有target，寻找左边界，第二种是确定有的情况下寻找右边界（注意找左边界的时候，由右侧逼近；找右边界的时候，由左侧逼近）；

class Solution {public int[] searchRange(int[] nums, int target) {int l = 0,r = nums.length-1;int[] res = new int[]{-1,-1};if (nums.length==0) return res;//寻找左边界  还没起确定有没有target 所以写法不太一样while (l<r){//结束时l==rint mid = l+(r-l)/2;if (nums[mid]>=target) r = mid;else l = mid+1;}if(nums[l]!=target) return res;//判断res[0] = l;r = nums.length-1;//寻找右边界，已经确定有target了while (l<=r){int mid = l+(r-l)/2;if(nums[mid]<=target) l = mid+1;else r = mid-1;}res[1] = r;return res;}
}

笨蛋写法

private int findFirstPosition(int[] nums, int target) {int left = 0;int right = nums.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] == target) {// ① 不可以直接返回，应该继续向左边找，即 [left, mid - 1] 区间里找right = mid - 1;} else if (nums[mid] < target) {// 应该继续向右边找，即 [mid + 1, right] 区间里找left = mid + 1;} else {// 此时 nums[mid] > target，应该继续向左边找，即 [left, mid - 1] 区间里找right = mid - 1;}}// 此时 left 和 right 的位置关系是 [right, left]，注意上面的 ①，此时 left 才是第 1 次元素出现的位置// 因此还需要特别做一次判断if (left != nums.length && nums[left] == target) {return left;}return -1;
}private int findLastPosition(int[] nums, int target) {int left = 0;int right = nums.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] == target) {// 只有这里不一样：不可以直接返回，应该继续向右边找，即 [mid + 1, right] 区间里找left = mid + 1;} else if (nums[mid] < target) {// 应该继续向右边找，即 [mid + 1, right] 区间里找left = mid + 1;} else {// 此时 nums[mid] > target，应该继续向左边找，即 [left, mid - 1] 区间里找right = mid - 1;}}// 由于 findFirstPosition 方法可以返回是否找到，这里无需单独再做判断return right;
}

5.带标记函数dp

689. 三个无重叠子数组的最大和

    /*  题目是求三个无重叠子数组的最大和
    其实可以拓展到N个无重叠子数组的最大和
    1，定义如下：
    sums[i]代表以nums[i]结尾的前k个数的和
    dp[i][j]代表截止到nums[i]形成的第j个无重叠子数组的最大和
    path[i][j]代表截止到nums[i]形成的第j个无重叠子数组以哪个下标为结尾，用来回溯路径
    2，状态转移方程为 dp[i][j] = max{dp[i - 1][j], sums[i] + dp[i - k][j - 1]};
    对应的path[i][j] = path[i - 1][j]或i
*/

//689. 三个无重叠子数组的最大和//典型带标记函数的动态规划 甚至和书上的都一样public int[] maxSumOfThreeSubarrays(int[] nums, int k){return maxSumOf_N_Subarrays(nums, k, 3);}public int[] maxSumOf_N_Subarrays(int[] nums, int k,int n) {int len = nums.length;if (k < 1 || n * k > len) return null;int sum = 0;int [] prekSum = new int[len];for (int i = 0; i < len; i++) {sum += nums[i];if (i >= k) sum -= nums[i-k];if (i >= k-1) prekSum[i] = sum;}int [][] dp = new int[len][n+1];//省去了边界处理int [][] path = new int[len][n+1];//初始值dp[k-1][1] = prekSum[k-1];path[k-1][1] = k-1;for (int i = k; i < len; i++) {for (int j = 1; j <= n; j++) {dp[i][j] = dp[i-1][j];path[i][j] = path[i-1][j];if (dp[i-k][j-1] + prekSum[i] > dp[i][j]){dp[i][j] = dp[i-k][j-1]+prekSum[i];path[i][j] = i;}}}int idx = n;int[] res = new int[n];int c = path[len-1][idx];res[idx-1] = c - k + 1;while (--idx>0){c = path[c-k][idx];res[idx-1] = c - k + 1;}return res;}

6.树

450. 删除二叉搜索树中的节点

    //450. 删除二叉搜索树中的节点public TreeNode deleteNode(TreeNode root, int key) {if (root==null) return null;if (key < root.val){root.left = deleteNode(root.left,key);}else if (key > root.val){root.right = deleteNode(root.right,key);}else{TreeNode left = root.left;TreeNode right = root.right;//寻找右侧最小的叶子节点if (right==null) return left;if (left==null) return right;while (right!=null && right.left!=null) right = right.left;//将root的左子树拼接到右侧最小叶子节点的左子树right.left = left;return root.right;}return root;}

7.  图论

Kruskal 算法

1584. 连接所有点的最小费用

class Solution {//Kruskal 算法public int minCostConnectPoints(int[][] points) {int n = points.length;int[] dist = new int[n];Arrays.fill(dist, Integer.MAX_VALUE);boolean[] added = new boolean[n];int ans = 0;for (int i = 0; i < n; i++) {int min = 0;// 1)选出最小边;for (int j = 0; j < n; j++) {if (!added[j] && dist[j] < dist[min]) {min = j;}}// 2)最小边加入生成树added[min] = true;if (dist[min] != Integer.MAX_VALUE) {ans += dist[min];}// 3)更新当前生成树到其他点的边的权值for (int j = 0; j < n; j++) {if (!added[j]) {dist[j] = Math.min(dist[j], mdist(points[min], points[j]));}}}return ans;}int mdist(int[] x, int[] y) {return Math.abs(x[0] - y[0]) + Math.abs(x[1] - y[1]);}
}

与上面相似的  迪杰斯特拉求最短路，下面给出邻接矩阵求法。

743. 网络延迟时间 

    // 743. 网络延迟时间// 单源最短路径问题public int networkDelayTime(int[][] times, int n, int k) {int inf = Integer.MAX_VALUE;int res = 0;// 1. 初始化邻接矩阵int [][] graph = new int[n+1][n+1];for (int i = 0; i <= n; i++) {for (int j = 0; j <= n; j++) {graph[i][j] = i == j ? 0 : inf;}}for (int[] edge : times) {graph[edge[0]][edge[1]] = edge[2];}// 2. 邻接矩阵查找各个顶点的极值// 初始化 距离数组 和 visitedint[] distance = new int[n+1];Arrays.fill(distance, inf);for (int i = 1; i <= n; i++) {distance[i] = graph[k][i];}boolean[] visited = new boolean[n+1];// 初始化源点visited[k] = true;distance[k] = 0;for (int i = 1; i <= n; i++) { // 代表循环次数为节点数量(每次找到一个最近点) 无实际意义int min = inf; // 当前最短路int idx = -1; // 最短路的节点for (int j = 1; j <= n; j++) {if (!visited[j] && distance[j] < min) {min = distance[j];idx = j;}}if (idx == -1) {break;}visited[idx] = true;for (int j = 1; j <= n; j++) {// 这里要加idx能到j的判断  不然有越界问题if (!visited[j] && graph[idx][j] != inf && distance[idx] + graph[idx][j] < distance[j]) {distance[j] = distance[idx] + graph[idx][j];}}}// 3. 取最大路径for (int i = 1; i <= n; i++) {res = Math.max(res, distance[i]);}return res == inf ? -1 : res;}

8.全排列问题

剑指 Offer 38. 字符串的排列

dfs是得到从 idx 处开始，后面字符的全排列；

    int n;vector<string> permutation(string s) {n = s.size();vector<string> res;dfs(s,res,0);return res;}void dfs(string s,vector<string> &res,int idx){if (idx == n){res.push_back(s);return;}//dfs将得到idx后的那些字符的全排列 每次只要取idx处的不同字符即可for (int i = idx;i<n;i++){bool flag = true;for (int j = idx;j<i;j++){if (s[i] == s[j]){//剪枝 此时j处字符等于i i已经被放到idx处过了flag = false;break;}}if (flag){swap(s[idx],s[i]);dfs(s,res,idx+1);swap(s[idx],s[i]);}}}

注意，上面的dfs的swap中递归调用函数时是从idx+1开始的，不是i+1，要理解递归函数的本质意义，像下面这个就是从i+1开始

39. 组合总和 允许重复

class Solution {
public:vector<vector<int>> res;vector<vector<int>> combinationSum(vector<int>& candidates, int target) {vector<int> tmp;//Arrays.sort(candidates.begin(),candidates.end());help(tmp,candidates,target,0);return res;}void help(vector<int> &tmp, vector<int>& candidates,int tar,int idx){if(tar==0){res.push_back(tmp);return;}for(int i = idx;i<candidates.size();i++){if(candidates[i]<=tar){tmp.push_back(candidates[i]);help(tmp,candidates,tar-candidates[i],i);tmp.pop_back();}}}
};

40. 组合总和 II 不允许重复

    vector<vector<int>> res;vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());vector<int> tmp;help(candidates,tmp,target,0);return res;}void help(vector<int>& candidates,vector<int>& tmp, int target,int idx){if(target==0){res.push_back(tmp);return;}if(idx==candidates.size()||candidates[idx]>target) return;for(int i = idx;i<candidates.size()&&candidates[i]<=target;i++){if(i>idx&&candidates[i]==candidates[i-1]) continue;tmp.push_back(candidates[i]);help(candidates,tmp,target-candidates[i],i+1);tmp.pop_back();}return;}