
在机器学习中,高维数据的分类问题非常具有挑战性。有时候,非常简单的问题会因为这个“维度诅咒”问题变得非常复杂。在本文中,我们将了解不同分类器的准确性和性能是如何变化的。
理解数据
对于本文,我们将使用Kaggle的“EEG Brainwave Dataset”(https://www.kaggle.com/birdy654/eeg-brainwave-dataset-feeling-emotions) 。该机器学习数据集包含来自EEG headset的电子脑电波信号,并且是时间格式的。
首先,让我们先读取数据,Python代码如下:
import pandas as pdbrainwave_df = pd.read_csv('../data/emotions.csv', index_col=False)brainwave_df.head()

该机器学习数据集中有2549列,“label”是我们分类问题的目标列。其他所有列,如“mean_d_1_a”、“mean_d2_a”等,都描述了脑电波信号读取的特征。以“fft”前缀开始的列很可能是原始信号的“快速傅里叶变换”。我们的目标列“label”描述了情绪的程度。
正如Kaggle所说,这是一个挑战:“我们能从脑电波读数预测情绪吗?”
让我们首先理解列'label'中的类分布,Python代码如下:
import seaborn as snsimport matplotlib.pyplot as pltplt.figure(figsize=(12,5))sns.countplot(x=brainwave_df.label, color='mediumseagreen')plt.title('Emotional sentiment class distribution', fontsize=16)plt.ylabel('Class Counts', fontsize=16)plt.xlabel('Class Label', fontsize=16)plt.xticks(rotation='vertical');
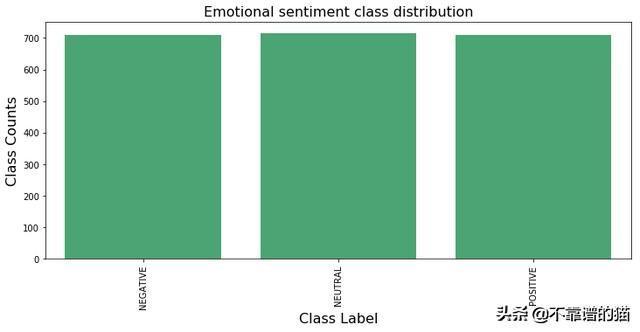
图1
因此,情绪有三个类别,“POSITIVE(正面)”,“NEGATIVE(负面)”和“NEUTRAL(中性)”。从条形图中可以清楚地看出,类分布没有偏态,它是一个带有目标变量“label”的“多类分类”问题。我们将尝试不同的分类器,看看准确度。
在应用任何分类器之前,应将“label”列与其他特征列分开('mean_d_1_a','mean_d2_a'等是特征)。
label_df = brainwave_df['label']brainwave_df.drop('label', axis = 1, inplace=True)brainwave_df.head()

由于这是一个“分类”问题,我们将按照以下约定对每个“分类器”进行尝试:
- 我们将在机器学习数据集上使用“交叉验证”(在我们的例子中将使用10 fold交叉验证)方法并取平均准确度。这将为我们提供分类器准确性的整体视图。
- 我们将使用基于“管道”的方法将所有预处理和主分类器计算结合起来。机器学习(ML)“管道”将所有处理阶段封装在一个单元中,并充当“分类器”本身。这样,所有阶段都可重用,并可用于形成其他“管道”。
- 我们将跟踪每种方法的构建和测试的总时间。
对于上述内容,我们将主要使用Python中的scikit-learn包。由于这里的特征数量非常多,因此将从一个适用于高维数据的分类器开始。
随机森林分类器
随机森林是一种基于树和bagging方法的集成分类器。采用概率熵计算方法,自动减少特征个数。让我们看看Python实现:
%%timefrom sklearn.pipeline import Pipelinefrom sklearn.ensemble import RandomForestClassifierfrom sklearn.model_selection import cross_val_score, train_test_splitpl_random_forest = Pipeline(steps=[('random_forest', RandomForestClassifier())])scores = cross_val_score(pl_random_forest, brainwave_df, label_df, cv=10,scoring='accuracy')print('Accuracy for RandomForest : ', scores.mean())

准确度非常好,达到97.7%,“总时间”非常短(仅限3.29秒)。
对于该分类器,不需要诸如缩放或噪声去除之类的预处理阶段,因为它完全基于概率并且完全不受缩放因子的影响。
逻辑回归分类器
“逻辑回归”是一种线性分类器,其工作方式与线性回归相同。
%%timefrom sklearn.pipeline import Pipelinefrom sklearn.preprocessing import StandardScalerfrom sklearn.linear_model import LogisticRegressionpl_log_reg = Pipeline(steps=[('scaler',StandardScaler()), ('log_reg', LogisticRegression(multi_class='multinomial', solver='saga', max_iter=200))])scores = cross_val_score(pl_log_reg, brainwave_df, label_df, cv=10,scoring='accuracy')print('Accuracy for Logistic Regression: ', scores.mean())

我们可以看到准确度(93.19%)低于'RandomForest','时间'更高(2分7秒)。
“逻辑回归”受到因变量的不同值范围的严重影响,因此强制“特征缩放”。这就是为什么来自scikit-learn的'StandardScaler'被添加为预处理阶段的原因。它根据具有零均值和单位方差的高斯分布自动缩放特征,因此所有变量的值范围从-1到+1。
花费大量时间的原因是因为高维性和缩放时间。数据集中有2549个变量,每个变量的系数应根据逻辑回归过程进行优化。此外,还有一个多重共线性的问题。这意味着线性相关变量应该组合在一起,而不是单独考虑它们。
多重共线性的存在影响准确性。所以现在的问题是,“我们能否减少变量的数量,减少多重共线性,并改善'花费的时间'呢?”
主成分分析(PCA)
PCA可以将原始的低级变量转换为更高维的空间,从而减少所需变量的数量。所有的共线性变量聚在一起。让我们做一个PCA的数据:
from sklearn.decomposition import PCAfrom sklearn.preprocessing import StandardScalerscaler = StandardScaler()scaled_df = scaler.fit_transform(brainwave_df)pca = PCA(n_components = 20)pca_vectors = pca.fit_transform(scaled_df)for index, var in enumerate(pca.explained_variance_ratio_): print("Explained Variance ratio by Principal Component 
:设计模式之工厂模式2)

理解)
打开cmd窗口)


:React中this.props.children续集)


)

:...数组拼接)





)
