🚀 优质资源分享 🚀
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| 🧡 Python实战微信订餐小程序 🧡 | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| 💛Python量化交易实战💛 | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
简介
复杂度分析法是对已知的代码进行效率分析的方法,与之相对的是使用实际数据运行代码的事后统计法。
复杂度分析法和事后统计法各有优劣,与复杂度分析法进行比较,事后统计法会有以下局限性:
- 测试结果非常依赖测试环境。硬件的不同会对测试结果有比较大的影响,比如不同处理器的执行时间会不一样
- 测试结果受数据的影响很大。对同一个排序算法,待排序数据的有序度会影响算法的执行时间;对于小规模的数据排序,插入排序的效率会比快速排序的效率更高
相比事后统计法,复杂度分析法更能表示一个算法在各个维度的综合性能。
复杂度
复杂度分为时间复杂度和空间复杂度,但是它们并不能准确地表示算法的执行时间和存储空间。
时间复杂度表示的是执行时间与数据规模之间的增长关系;空间复杂度表示的是存储空间与数据规模之间的增长关系。
复杂度表示法
常用的复杂度表示法就是大 O 复杂度表示法,时间复杂度和空间复杂度都能运用这个概念,在概念上可以进行类比。
在实际使用中,空间复杂度会比时间复杂度更简单些,下面只对时间复杂度做解析。
大 O 时间复杂度表示法
| | int cal(int n) { |
| | int sum = 0; |
| | int i = 1; |
| | for (; i <= n; ++i) { |
| | sum = sum + i; |
| | } |
| | return sum; |
| | } |对上述代码着手,解析这段代码的时间复杂度。
第 2 行和第 3 行仅会运行一次,但第 4、5、6 行是一个 for 循环,将会运行 n 次,因此,整个函数运行的次数可以简单地认为是 n + 2 次。
假如将一行代码的执行时间算作单位时间,以此做类比,则此函数的执行时间 T(n) 与代码的执行次数 n 成正比:
T(n)=O(f(n))其中,n 表示数据规模的大小;f(n) 表示每行代码执行的次数总和,因为这是一个公式,所以用 f(n) 来表示;T(n) 表示代码执行的时间。公式中的 O 表示代码的执行时间 T(n) 与 f(n) 表达式成正比。
大 O 时间复杂度实际上并不具体表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势。
所以,大 O 时间复杂度也叫作渐进时间复杂度(asymptotic time complexity),简称时间复杂度。
从定义上理解,大 O 符号是一种算法「复杂度」的「相对」「表示」方式:
- 复杂度:表示相对其他东西的度量结果
- 相对:只能比较相同的事物,不能将一个做算数乘法的算法和排序整数列表的算法进行比较
- 表示:大 O 符号把算法间的比较简化为一个单一变量
时间复杂度分析
变量法则
代码中的变量决定时间复杂度。
大 O 复杂度表示法是一种函数的表示方式,函数中存在至少一个变量,这其实就说明了大 O 复杂度表示法展示了代码执行时间随数据规模增长的变化趋势。
所以,在分析时间复杂度的时候,需要记住代码中的变量决定时间复杂度,观察代码中具体哪一个数据变量在实际运行中最能体现运行时间的趋势。
加法法则
总复杂度等于量级最大的那段代码的复杂度。
大 O 复杂度表示法只是表示一种变化趋势,一般认为,与公式中的高阶 n 值相比,常量、系数、低阶量级与算法的增长趋势关系不大。
为了降低复杂性以及提高对比性,通常会忽略掉公式中的常量、系数、低阶,只记录其中最大阶的量级即可。
因此,在分析一个算法、一段代码的时间复杂度时,一般只需关注循环执行次数最多的那一段代码即可。
通常,核心代码执行次数的 n 的量级,就是整段要分析代码的时间复杂度。
乘法法则
嵌套代码的复杂度等于嵌套内外代码复杂度的乘积。
在实际开发中,嵌套循环的代码比较常见,这里涉及到嵌套循环的时间复杂度分析。
如果把一次循环看作是 n 次,每次循环当中又会再做一次内循环,再把这次内循环看作是 m 次,这样整体循环就可以看作是 n×m 次,这就是乘法法则。
大部分算法复杂度分析中,会经常遇到如 n2、n3 这样的时间复杂度,也使用到乘法法则。
常见时间复杂度
常见的时间复杂度有很多,如 O(1)、O(logn)、O(n)、 O(nlogn)、O(n2)、O(n3)、O(nk)、O(2n)、O(n!) 等。
时间复杂度可以分为多项式量级和非多项式量级两种,多项式量级指的是以 n 作为底数,非多项式量级指的是不以 n 作为底数的非确定量级。
当数据规模 n 越来越大时,非多项式量级算法的执行时间会急剧增加,求解问题的执行时间会无限增长。
因此,非多项式时间复杂度的算法是非常低效的算法,实际编码中需要尽量避免这种情况出现。
常见的时间复杂度中,非多项式量级只有 O(2n)、O(n!) 两个,其他的都是多项式量级。
其实,时间复杂度超过 O(nlogn) 的算法就可以称为指数级增长的算法,应尽量避免。
常量级
O(1) 是常量级时间复杂度的一种表示方式,只要代码的执行时间不随 n 的增大而增长,这样代码的时间复杂度就被记作 O(1)。
一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是 O(1)。
对数级
对数级时间复杂度非常常见,同时也是最难分析的一种时间复杂度。
实际上,不管是以 2 为底、以 3 为底,还是以 10 为底,都可以把所有对数阶的时间复杂度都记为 O(logn)。
O(log3n)=O(log32)×O(log2n) => O(log3n)=O(C×log2n),其中 C=log32 是一个常量可忽略不计。
如果一段代码的时间复杂度是 O(logn),然后代码循环执行 n 遍,这段代码就是 O(nlogn) 的时间复杂度。
O(nlogn) 也是一种常见的算法时间复杂度。比如归并排序、快速排序的平均时间复杂度都是 O(nlogn)。
多变量级
顾名思义,多变量级时间复杂度受多个变量影响,表示一个时间复杂度由多个数据的规模来决定。
这种情况不能随意使用加法法则省略掉其中一个,而是两个变量都需要使用到,如 O(m×n)、O(m+n) 都是多变量级的复杂度。
时间复杂度维度
最好情况时间复杂度
最好情况时间复杂度就是,在最理想的情况下,执行这段代码的时间复杂度。
最坏情况时间复杂度
最坏情况时间复杂度就是,在最糟糕的情况下,执行这段代码的时间复杂度。
平均时间复杂度
平均时间复杂度会将所有可能情况下的执行次数和其发生的频率聚合起来计算加权平均值,这里涉及到概率论的知识,因此平均时间复杂度又被称为加权平均时间复杂度、期望时间复杂度。
均摊时间复杂度
均摊时间复杂度是一种适用场景更少的表示方式,对于某些特殊的场景(比如一种场景是大部分情况下时间复杂度都很低,只有个别情况下时间复杂度比较高,而且这些操作之间存在前后连贯的时序关系),可以引入摊还分析法计算得出均摊时间复杂度。
对于上面描述的场景,可以将这一组操作放在一起分析,尝试将较高时间复杂度那次操作的耗时平摊到其他那些时间复杂度较低的操作上。
均摊时间复杂度是一种特殊的平均时间复杂度。通常,在能够应用均摊时间复杂度分析的场合,一般均摊时间复杂度就等于最好情况时间复杂度。
复杂度变化趋势
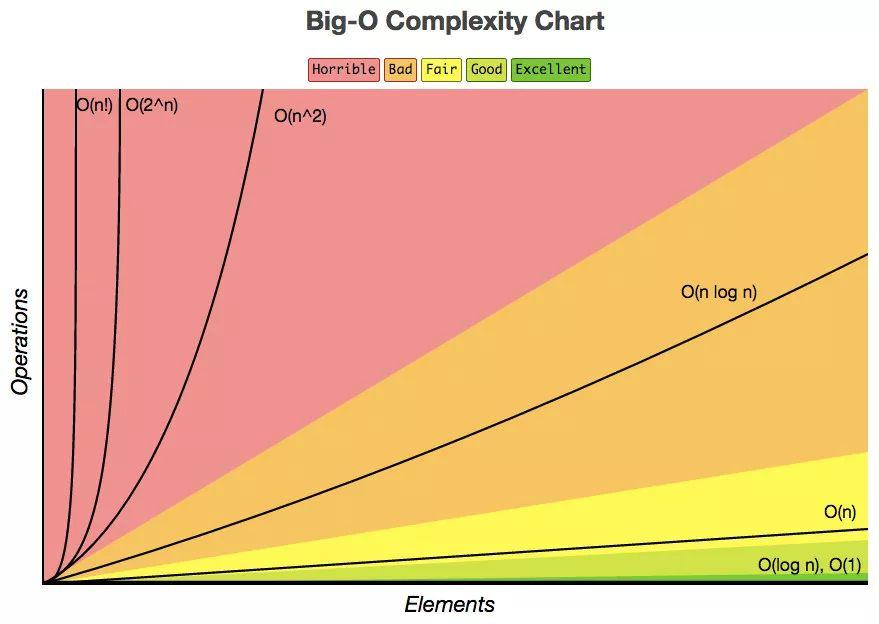
上图是常见复杂度的变化趋势,可以清晰地看到,超过 O(nlogn) 的复杂度就可以随着 n 的变化而急剧变化,在实际开发中,应尽量避免。



时钟配置和闪烁LED)


---A. Lights Out)

)

GPIO)


认识中断)




UART通信)
