源码

FFT.c

/*********************************************************************
快速傅里叶变换C程序包
函数简介：此程序包是通用的快速傅里叶变换C语言函数，移植性强，以下部分不依
赖硬件。此程序包采用联合体的形式表示一个复数，输入为自然顺序的复
数（输入实数是可令复数虚部为0），输出为经过FFT变换的自然顺序的
复数.此程序包可在初始化时调用create_sin_tab()函数创建正弦函数表，
以后的可采用查表法计算耗时较多的sin和cos运算，加快可计算速度.与
Ver1.1版相比较，Ver1.2版在创建正弦表时只建立了1/4个正弦波的采样值，
相比之下节省了FFT_N/4个存储空间
使用说明：使用此函数只需更改宏定义FFT_N的值即可实现点数的改变，FFT_N的
应该为2的N次方，不满足此条件时应在后面补0。若使用查表法计算sin值和
cos值，应在调用FFT函数前调用create_sin_tab()函数创建正弦表
函数调用：FFT(Compx);
作    者：吉帅虎
时    间：2010-2-20
版    本：Ver1.2
参考文献：
**********************************************************************/
#include <math.h>
#include "FFT.h"struct compx Compx[FFT_N] = {0};		//FFT输入和输出：从Compx[0]开始存放，根据大小自己定义
double SIN_TAB[FFT_N / 4 + 1];			//定义正弦表的存放空间/*******************************************************************
函数原型：struct compx EE(struct compx b1,struct compx b2)
函数功能：对两个复数进行乘法运算
输入参数：两个以联合体定义的复数a,b
输出参数：a和b的乘积，以联合体的形式输出
*******************************************************************/
struct compx EE(struct compx a, struct compx b)
{struct compx c;c.real = a.real*b.real - a.imag*b.imag;c.imag = a.real*b.imag + a.imag*b.real;return(c);
}/******************************************************************
函数原型：void create_sin_tab(double *sin_t)
函数功能：创建一个正弦采样表，采样点数与福利叶变换点数相同
输入参数：*sin_t存放正弦表的数组指针
输出参数：无
******************************************************************/
void create_sin_tab(double *sin_t)
{int i;for (i = 0; i <= FFT_N / 4; i++)sin_t[i] = sin(2 * PI*i / FFT_N);
}
/******************************************************************
函数原型：void sin_tab(double pi)
函数功能：采用查表的方法计算一个数的正弦值
输入参数：pi 所要计算正弦值弧度值，范围0--2*PI，不满足时需要转换
输出参数：输入值pi的正弦值
******************************************************************/
double sin_tab(double pi)
{int n;double a = 0;n = (int)(pi*FFT_N / 2 / PI);if (n >= 0 && n <= FFT_N / 4)a = SIN_TAB[n];else if (n>FFT_N / 4 && n<FFT_N / 2){n -= FFT_N / 4;a = SIN_TAB[FFT_N / 4 - n];}else if (n >= FFT_N / 2 && n<3 * FFT_N / 4){n -= FFT_N / 2;a = -SIN_TAB[n];}else if (n >= 3 * FFT_N / 4 && n<3 * FFT_N){n = FFT_N - n;a = -SIN_TAB[n];}return a;
}
/******************************************************************
函数原型：void cos_tab(double pi)
函数功能：采用查表的方法计算一个数的余弦值
输入参数：pi 所要计算余弦值弧度值，范围0--2*PI，不满足时需要转换
输出参数：输入值pi的余弦值
******************************************************************/
double cos_tab(double pi)
{double a, pi2;pi2 = pi + PI / 2;if (pi2>2 * PI)pi2 -= 2 * PI;a = sin_tab(pi2);return a;
}
/*****************************************************************
函数原型：void FFT(struct compx *xin)
函数功能：对输入的复数组进行快速傅里叶变换（FFT）
输入参数：*xin复数结构体组的首地址指针，struct型
输出参数：无
*****************************************************************/
void FFT(struct compx *xin)
{register int f, m, nv2, nm1, i, k, l, j = 0;struct compx u, w, t;nv2 = FFT_N / 2;					//变址运算，即把自然顺序变成倒位序，采用雷德算法nm1 = FFT_N - 1;for (i = 0; i < nm1; ++i){if (i < j)						//如果i<j,即进行变址{t = xin[j];xin[j] = xin[i];xin[i] = t;}k = nv2;						//求j的下一个倒位序while (k <= j)					//如果k<=j,表示j的最高位为1{j = j - k;					//把最高位变成0k = k / 2;					//k/2，比较次高位，依次类推，逐个比较，直到某个位为0}j = j + k;						//把0改为1}{int le, lei, ip;				//FFT运算核，使用蝶形运算完成FFT运算f = FFT_N;for (l = 1; (f = f / 2) != 1; ++l);				//计算l的值，即计算蝶形级数for (m = 1; m <= l; m++)						// 控制蝶形结级数{   //m表示第m级蝶形，l为蝶形级总数l=log（2）Nle = 2 << (m - 1);							//le蝶形结距离，即第m级蝶形的蝶形结相距le点lei = le / 2;                               //同一蝶形结中参加运算的两点的距离u.real = 1.0;								//u为蝶形结运算系数，初始值为1u.imag = 0.0;w.real = cos_tab(PI / lei);					//w为系数商，即当前系数与前一个系数的商w.imag = -sin_tab(PI / lei);for (j = 0; j <= lei - 1; j++)				//控制计算不同种蝶形结，即计算系数不同的蝶形结{for (i = j; i <= FFT_N - 1; i = i + le)	//控制同一蝶形结运算，即计算系数相同蝶形结{ip = i + lei;						//i，ip分别表示参加蝶形运算的两个节点t = EE(xin[ip], u);					//蝶形运算，详见公式xin[ip].real = xin[i].real - t.real;xin[ip].imag = xin[i].imag - t.imag;xin[i].real = xin[i].real + t.real;xin[i].imag = xin[i].imag + t.imag;}u = EE(u, w);							//改变系数，进行下一个蝶形运算}}}
}/*****************************************************************
函数原型：void Get_Result(struct compx *xin, double sample_frequency)
函数功能：求变换后结果的模值，存入复数的实部部分，频率存入复数的虚数部分，有效数据为前FFT_N/2个数
输入参数：*xin复数结构体组的首地址指针，struct型, sample_frequency: 采样频率
输出参数：无
*****************************************************************/
void Get_Result(struct compx *xin, double sample_frequency)
{int i = 0;for (i = 0; i < FFT_N / 2; ++i){          //求变换后结果的模值，存入复数的实部部分xin[i].real = sqrt(xin[i].real*xin[i].real + xin[i].imag*xin[i].imag) / (FFT_N >> (i != 0));xin[i].imag = i * sample_frequency / FFT_N;}
}/*****************************************************************
函数原型：void Refresh_Data(struct compx *xin, double wave_data)
函数功能：更新数据
输入参数：*xin复数结构体组的首地址指针, struct型, id: 标号, wave_data: 一个点的值
输出参数：无
*****************************************************************/
void Refresh_Data(struct compx *xin, int id, double wave_data)
{xin[id].real = wave_data;xin[id].imag = 0;
}

FFT.h

#ifndef FFT_H
#define FFT_H#define FFT_N 16                                        //定义傅里叶变换的点数
#define PI 3.14159265358979323846264338327950288419717  //定义圆周率值struct compx { double real, imag; };                    //定义一个复数结构extern struct compx Compx[];							//FFT输入和输出：从Compx[0]开始存放，根据大小自己定义
extern double SIN_TAB[];								//正弦信号表extern void Refresh_Data(struct compx *xin, int id, double wave_data);
extern void create_sin_tab(double *sin_t);
extern void FFT(struct compx *xin);
extern void Get_Result(struct compx *xin, double sample_frequency);#endif

使用方法

在FFT.h中修改 FFT_N 16，定义傅里叶变换的点数，由于FFT变换归一化后，除了0Hz的直流分量外，整个结果表是对称的，即若点数为16，则我们只看前8个点即可，所以这个傅里叶变换的点数可根据你的屏幕长方向上的像素数来决定，如128x64的屏幕可以考虑使用256点的FFT，我这里使用8x8的LED点阵屏来显示，故使用16点的FFT。

在运算前需调用一次 create_sin_tab(SIN_TAB) 建立正弦信号表, 之后将用查表法计算正弦值，加速计算

使用 Refresh_Data (Compx, i, wave_data)函数填入数据后

调用 FFT(Compx) 即可完成变换

使用 Get_Result (Compx, Sample_Frequency)函数求变换后结果的模值，存入复数的实部部分，频率存入复数的虚数部分，有效数据为前FFT_N/2个数

	#define Sample_Frequency 800			//采样频率 800Hz#define Frequency 100					//测试信号 100Hzfor (i = 0; i < FFT_N; ++i)				//使用Refresh_Data(Compx, i, wave_data)函数填入数据，这里建立一个100Hz的方波测试信号{ if (sin(2 * PI * Frequency * i / Sample_Frequency) > 0)Refresh_Data(Compx, i, 1);else if (sin(2 * PI * Frequency * i / Sample_Frequency) < 0)Refresh_Data(Compx, i, -1);elseRefresh_Data(Compx, i, 0);}										create_sin_tab(SIN_TAB);				//建立正弦信号表, 之后将用查表法计算正弦值，加速计算FFT(Compx);								//快速傅里叶变换Get_Result(Compx, Sample_Frequency);	//求变换后结果的模值，存入复数的实部部分，频率存入复数的虚数部分，有效数据为前FFT_N/2个数

效果

在这里插入图片描述
计算频率的方法：
采样频率为800Hz，共16个点，故一格 = 800Hz / 16 = 50 Hz
如图，在第三格和第七格各有一个峰，则对应的频率是2 x 50Hz = 100Hz 和 6 x 50Hz = 300Hz，该结果已由Get_Result函数计算并存在原数组的虚部中。

物理意义的解读见如何 FFT(快速傅里叶变换) 求幅度、频率（超详细含推导过程）—— Xav Pan

性能
晶振频率 11.0592MHz 6T模式（22.1184MHz 12T）
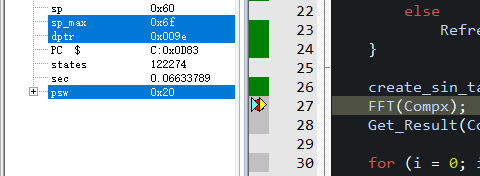
仿真下花费约 0.13222819 - 0.06633789 = 0.0658903 (s)
即完成一次16点的FFT变换，11.0592MHz 6T的51单片机花费 65.8903 ms
在这里插入图片描述

同样的程序，使用Vs 2015 跑65536个点的计算结果：

同样的数据使用python计算800个点的结果：
来源：使用python（scipy和numpy）实现快速傅里叶变换（FFT）最详细教程 —— LoveMIss-Y
在这里插入图片描述

其他部分的代码

点阵屏部分代码见【51单片机快速入门指南】2.4：IO扩展(串转并) 与 LED点阵屏

main.c

#include <REGX52.H>
#include "intrins.h"
#include "stdint.h"
#include "FFT.h"
#include <math.h>
#include "HC74595.h"void main(void)
{uint8_t i, j; double Largest = 0;#define Sample_Frequency 800			//采样频率 800Hz#define Frequency 100					//测试信号 100Hzfor (i = 0; i < FFT_N; ++i)				//使用Refresh_Data(Compx, i, wave_data)函数填入数据，这里建立一个100Hz的方波信号{ if (sin(2 * PI * Frequency * i / Sample_Frequency) > 0)Refresh_Data(Compx, i, 1);else if (sin(2 * PI * Frequency * i / Sample_Frequency) < 0)Refresh_Data(Compx, i, -1);elseRefresh_Data(Compx, i, 0);}										create_sin_tab(SIN_TAB);				//建立正弦信号表, 之后将用查表法计算正弦值，加速计算FFT(Compx);								//快速傅里叶变换Get_Result(Compx, Sample_Frequency);	//求变换后结果的模值，存入复数的实部部分，频率存入复数的虚数部分，有效数据为前FFT_N/2个数for (i = 0; i < FFT_N / 2; ++i)			//将计算结果处理成图像的部分{         if(Compx[i].real > Largest)Largest = Compx[i].real;}for(i = 0; i < 8; ++i){for(j = 0; j < (uint8_t)((Compx[i].real / Largest) * 8 + 0.5); ++j)Mat[8 - j - 1][i] = 1;}while(1){imshow(Mat);						//显示图像}
}