目录
- 源码
- FFT.c
- FFT.h
- 使用方法
- 初始化
- 输入数据
- FFT 快速傅里叶变换
- 解算FFT结果
- 使用python绘制FFT波形
- IFFT 快速傅里叶逆变换
- 解算IFFT结果
Windows 10 20H2
Visual Studio 2015
Python 3.8.12 (default, Oct 12 2021, 03:01:40) [MSC v.1916 64 bit (AMD64)] :: Anaconda, Inc. on win32
小改自用于ARM上的FFT与IFFT源代码(C语言,不依赖特定平台)—— syrchina V6.55版,其V6.6版改用了动态内存分配,可能不适用于部分单片机平台。
要使用窗函数处理,见常见窗函数的C语言实现及其形状,适用于单片机、DSP作FFT运算
经过仔细阅读和测试,syrchina大佬的版本(2011.05.22)应该是优化自吉帅虎大佬的版本(2010.2.20),主要是优化了查表和蝶形算法的部分,在VS2015中Debug模式下计算一轮1024点的FFT足足快了几乎一倍,且它们的输出结果是一样的。syrchina大佬的版本附有IFFT的算法,故这里稍作修改,做个记录,供以后使用。
吉帅虎版
syrchina版
源码
FFT.c
#include "FFT.h"Complex data_of_N_FFT[FFT_N]; //定义存储单元,原始数据与复数结果均使用之
double SIN_TABLE_of_N_FFT[FFT_N / 4 + 1];//创建正弦函数表 初始化FFT程序
void Init_FFT(void)
{int i;for (i = 0; i <= FFT_N / 4; i++){SIN_TABLE_of_N_FFT[i] = sin(2 * i * PI / FFT_N);}
}double Sin_find(double x)
{int i = (int)(FFT_N * x); //注意:i已经转化为0~N之间的整数了! i = i >> 1; // i = i / 2;if (i > FFT_N / 4){ //根据FFT相关公式,sin()参数不会超过PI, 即i不会超过N/2 i = FFT_N / 2 - i;//i = i - 2*(i-Npart4);}return SIN_TABLE_of_N_FFT[i];
}double Cos_find(double x)
{int i = (int)(FFT_N*x);//注意:i已经转化为0~N之间的整数了! i = i >> 1;if (i < FFT_N / 4){ //不会超过N/2 return SIN_TABLE_of_N_FFT[FFT_N / 4 - i];}else //i > Npart4 && i < N/2 {return -SIN_TABLE_of_N_FFT[i - FFT_N / 4];}
}//变址
void ChangeSeat(Complex *DataInput)
{int nextValue, nextM, i, k, j = 0;Complex temp;nextValue = FFT_N / 2; //变址运算,即把自然顺序变成倒位序,采用雷德算法nextM = FFT_N - 1;for (i = 0; i < nextM; i++){if (i < j) //如果i<j,即进行变址{temp = DataInput[j];DataInput[j] = DataInput[i];DataInput[i] = temp;}k = nextValue; //求j的下一个倒位序while (k <= j) //如果k<=j,表示j的最高位为1{j = j - k; //把最高位变成0k = k / 2; //k/2,比较次高位,依次类推,逐个比较,直到某个位为0}j = j + k; //把0改为1}
}//FFT运算函数
void FFT(void)
{int L = FFT_N, B, J, K, M_of_N_FFT;int step, KB;double angle;Complex W, Temp_XX;ChangeSeat(data_of_N_FFT); //变址 //CREATE_SIN_TABLE();for (M_of_N_FFT = 1; (L = L >> 1) != 1; ++M_of_N_FFT); //计算蝶形级数for (L = 1; L <= M_of_N_FFT; L++){step = 1 << L; //2^LB = step >> 1; //B=2^(L-1)for (J = 0; J < B; J++){//P = (1<<(M-L))*J;//P=2^(M-L) *J angle = (double)J / B; //这里还可以优化 W.real = Cos_find(angle); //使用C++时该函数可声明为inline W.real = cos(angle*PI);W.imag = -Sin_find(angle); //使用C++时该函数可声明为inline W.imag = -sin(angle*PI);for (K = J; K < FFT_N; K = K + step){KB = K + B;//Temp_XX = XX_complex(data[KB],W); 用下面两行直接计算复数乘法,省去函数调用开销 Temp_XX.real = data_of_N_FFT[KB].real * W.real - data_of_N_FFT[KB].imag*W.imag;Temp_XX.imag = W.imag*data_of_N_FFT[KB].real + data_of_N_FFT[KB].imag*W.real;data_of_N_FFT[KB].real = data_of_N_FFT[K].real - Temp_XX.real;data_of_N_FFT[KB].imag = data_of_N_FFT[K].imag - Temp_XX.imag;data_of_N_FFT[K].real = data_of_N_FFT[K].real + Temp_XX.real;data_of_N_FFT[K].imag = data_of_N_FFT[K].imag + Temp_XX.imag;}}}
}//IFFT运算函数
void IFFT(void)
{int L = FFT_N, B, J, K, M_of_N_FFT;int step, KB;double angle;Complex W, Temp_XX;ChangeSeat(data_of_N_FFT);//变址 for (M_of_N_FFT = 1; (L = L >> 1) != 1; ++M_of_N_FFT); //计算蝶形级数for (L = 1; L <= M_of_N_FFT; L++){step = 1 << L; //2^LB = step >> 1; //B=2^(L-1)for (J = 0; J<B; J++){angle = (double)J / B; //这里还可以优化 W.real = Cos_find(angle); //使用C++时该函数可声明为inline W.real = cos(angle*PI);W.imag = Sin_find(angle); //使用C++时该函数可声明为inline W.imag = sin(angle*PI);for (K = J; K < FFT_N; K = K + step){KB = K + B;//用下面两行直接计算复数乘法,省去函数调用开销 Temp_XX.real = data_of_N_FFT[KB].real * W.real - data_of_N_FFT[KB].imag*W.imag;Temp_XX.imag = W.imag*data_of_N_FFT[KB].real + data_of_N_FFT[KB].imag*W.real;data_of_N_FFT[KB].real = data_of_N_FFT[K].real - Temp_XX.real;data_of_N_FFT[KB].imag = data_of_N_FFT[K].imag - Temp_XX.imag;data_of_N_FFT[K].real = data_of_N_FFT[K].real + Temp_XX.real;data_of_N_FFT[K].imag = data_of_N_FFT[K].imag + Temp_XX.imag;}}}
}/*****************************************************************
函数原型:void Refresh_Data(int id, double wave_data)
函数功能:更新数据
输入参数:id: 标号; wave_data: 一个点的值
输出参数:无
*****************************************************************/
void Refresh_Data(int id, double wave_data)
{data_of_N_FFT[id].real = wave_data;data_of_N_FFT[id].imag = 0;
}
FFT.h
#ifndef FFT_H_
#define FFT_H_#include <math.h>#define PI 3.14159265358979323846264338327950288419716939937510 //圆周率#define FFT_N 1024 //傅里叶变换的点数 #define FFT_RESULT(x) (sqrt(data_of_N_FFT[x].real*data_of_N_FFT[x].real+data_of_N_FFT[x].imag*data_of_N_FFT[x].imag)/ (FFT_N >> (x != 0)))
#define FFT_Hz(x, Sample_Frequency) ((double)(x * Sample_Frequency) / FFT_N)#define IFFT_RESULT(x) (data_of_N_FFT[x].real / FFT_N)typedef struct //定义复数结构体
{double real, imag;
}Complex;extern Complex data_of_N_FFT[];
extern double SIN_TABLE_of_N_FFT[];void Init_FFT(void);
void FFT(void);
void IFFT(void);
void Refresh_Data(int id, double wave_data);#endif // !FFT_H_
使用方法
初始化
在FFT.h中修改FFT的点数
由于FFT变换归一化后,除了0Hz的直流分量外,整个结果表是对称的,即若点数为1024,则我们只看前512个点即可,所以这个傅里叶变换的点数可根据你的屏幕长方向上的像素数来决定,如128x64的屏幕可以考虑使用256点的FFT。
#define FFT_N 1024 //傅里叶变换的点数
初始化一遍,生成正弦表
Init_FFT(); //①初始化各项参数,此函数只需执行一次 ; 修改FFT的点数去头文件的宏定义处修改
输入数据
这里设采样频率为100Hz,产生一个0~5V,10Hz方波
void Refresh_Data(int id, double wave_data);
#define Sample_Frequency 100for (i = 0; i < FFT_N; i++)//制造输入序列 {if (sin(2 * PI * 10 * i / Sample_Frequency) > 0)Refresh_Data(i, 5);else if (sin(2 * PI * 10 * i / Sample_Frequency) < 0)Refresh_Data(i, 0);elseRefresh_Data(i, 2.5);}
FFT 快速傅里叶变换
FFT(); //③进行 FFT计算
解算FFT结果
使用 FFT_Hz (i, Sample_Frequency) 获取该点频率
使用 FFT_RESULT (i) 获取该点模值
由于FFT结果是对称的,故只需看前FFT_N / 2个点
我这里为了看波形用C++跑的,将生成的坐标保存进out.txt中
#include <iostream>
#include <fstream>
using namespace std;
ofstream out;out.open("out.txt");for (int i = 0; i < FFT_N / 2; ++i){out << FFT_Hz(i, Sample_Frequency) << " " << FFT_RESULT(i) << endl;}out.close();
使用python绘制FFT波形
import matplotlib.pyplot as pltx = []
y = []with open(r'D:\out.txt的路径\out.txt') as TXT_File:for line in TXT_File:tmp = line.split()x.append(float(tmp[0]))y.append(float(tmp[1]))fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(x, y)
plt.show()

IFFT 快速傅里叶逆变换
IFFT();//进行 IFFT计算
解算IFFT结果
使用 IFFT_RESULT (i) 读取每个点的波形
我这里同样为了看波形将生成的坐标保存进out1.txt中
ofstream out1;out1.open("out1.txt");for (int i = 0; i < FFT_N; ++i){out1 << i << " " << IFFT_RESULT(i) << endl;}out1.close();
可以看到,又转变回0~5V的方波了,故也许可以FFT后直接对特定频率的信号处理再逆变换回去,实现滤波。
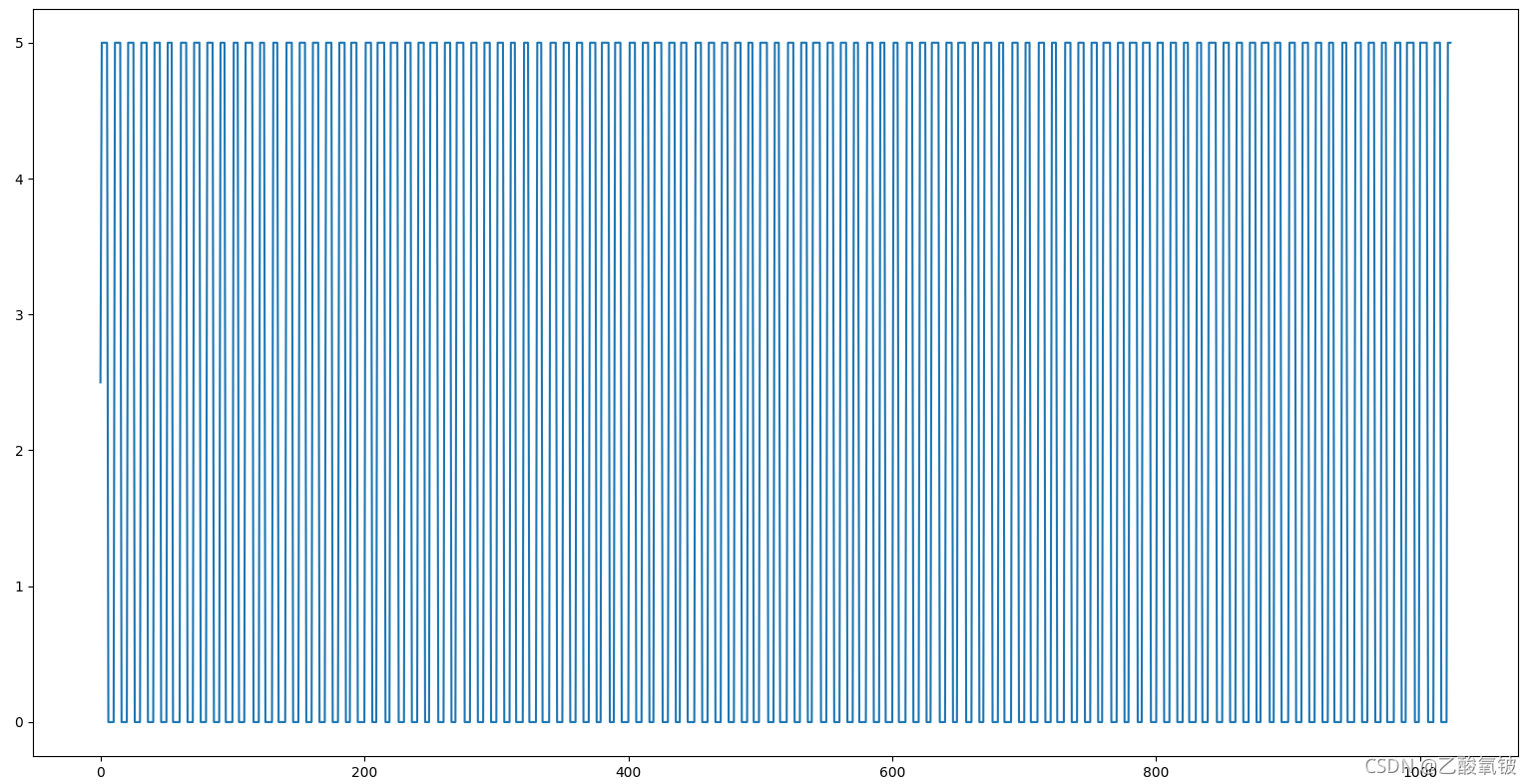
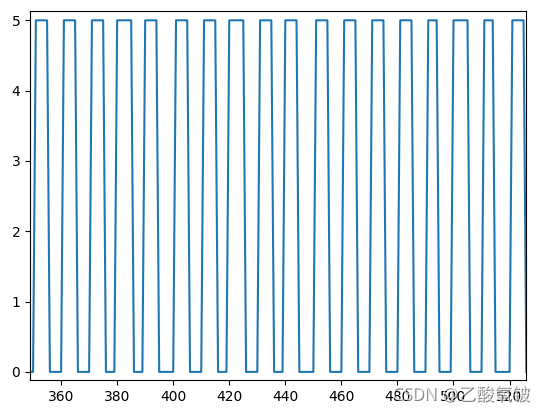
)




)






...)
锁简析)





)