2 概述

2.1 模型概述

2.1.1 预测房价问题

在我们要开始下面的问题前，我们先来看一些关于房价预测的例子。

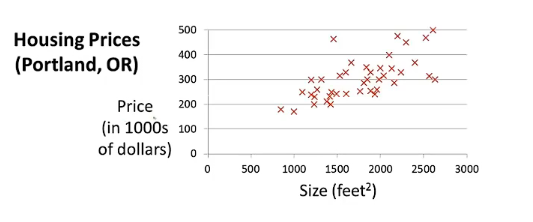
假设我们有一个朋友，它想要卖掉房子，而房子的大小是1250平方英尺，你想要告诉它们，你的房子能够卖多少钱。那你说出这句话的依据请问是什么？是猜测吗？显然不是。我们通过某个确定的模型，根据所拥有的数据集来确定一个具体的函数，然后根据这个函数输入房子的大小，然后输出房子卖出大概的估价，这也是你对朋友说这话的底气。

上面的问题实际上是一个有监督学习，因为它有确定的模型来给我们算出对应的函数，而它实际上又是一个回归问题，这是因为根据算出来的函数，我们可以通过连续地输入特征值来获取自己想要的预测值。

还是上面的例子，我们说了我们是通过已有的数据集来训练模型使其变为确定的函数，那么这部分拿来训练模型的数据集我们称之为训练集。

2.1.2 符号

在机器学习中我们会用到许许多多的符号，我们在这里先挑出几个比较常见的符号。

我们一般习惯用m来表示训练集的数目。用$x_n$来表示某一个样本的某一个特征，而用y来表示样本对应的输出，用$\hat{y}$来代表我们在训练好的模型上通过输入获得相应的预测值。

由于训练集中有多个样本，所以我们一般用$(x^i,y^i)$来表示第i个样本的特征和第i个样本对应的输出。

在这一讲下面的学习中，我们会用到最简单的模型来开始我们的机器学习之路，即线性回归模型。

2.2 代价函数

在这一小节中，我们来试着定义代价函数这一名词。代价函数也叫损失函数，你懂得，这是因为中文的多义性，它英文名实际上为loss function。

我们依旧使用2.1用过的例子来讲述我们接下来要探讨的问题，假如我们有m为47的样本数，我们采用的模型是线性模型，其中${\theta }_1$如同我们初中第一次学习一次函数中的k，而${\theta }_0$为b。但是我们后面不会用到k和b了，你要记住这是机器学习，符号的改变并不会影响最基本的思路。

在这个假定的模型中，我们要求的是一个具体的函数，即我们要求出${\theta }_0和{\theta }_1$的值。因为x是特征，y是预测，对吧？

但是这个${\theta }_0和{\theta }_1$并没有你想象的那么好选择，试想，如果你的${\theta }_0和{\theta }_1$选出来不能很好地去预测新的输入，那不就废了吗。而这个衡量能不能很好预测的标准就是，我们根据训练集训练出来的函数模型预测出来的结果和真实结果偏差应该尽可能的小。即$y和\hat{y}$之间的误差应该尽可能地小。

我们需要讨论一个问题，这个$y和\hat{y}$之间的误差用什么来衡量呢？$y-\hat{y}$吗？显然不是，因为它们的差值有可能出现负数，这对我们后续的计算可能造成干扰。实际上，误差有多种衡量方式，由于考虑到我们刚刚入门，所以我们采用最简单的平方误差来进行误差上的衡量。平方误差的表现形式是：$(\hat{y}-y{)}^2$，而我们有多个样本，所以需要对误差求总和然后计算平均误差，即$\frac{1}{m}(\hat{y}-y{)}^2$。

求最小值怎么求？在高中数学学习的过程中，我们可以总结出几种求最值的方法：

• 二次函数公式
• 基本不等式
• 求导
• …

在这里我们选择求导比较方便，而为了便于求导，我们将上面的公式改写为：$\frac{1}{2m}(\hat{y}-y{)}^2$，所以为了找出符合我们心中所想的那个函数，我们必须对这个损失函数$J({\theta }_0,{\theta }_1)=\frac{1}{2m}(\hat{y}-y{)}^2$进行最小化。

2.3 代价函数的用处

在上一小节中，我们提到了代价函数的数学形式，在这一小节中，我们会详细提到代价函数是用来做什么呢。

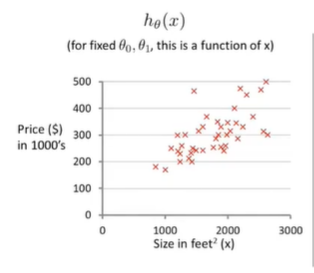
由于前面我们给定的模型是$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$，参数太多对新手不是很友好，所以我们把这个函数模型再简化一下变成$h_{\theta }(x)={\theta }_{1}x$。那么这个损失函数J就变为$J({\theta }_1)=\frac{1}{2m}(\hat{y}-y{)}^2$。

当我们${\theta }_1$取0.5时，两个函数的图像如下图所示：

也就是说，通过不同的${\theta }_1$的取值，如果其$J({\theta }_1)$的值越小，那么说明其画出来的函数直线更够更好的拟合所有的数据集。

$J({\theta }_1)$什么时候最小？我们可以根据求导来获取它的极小值。而为什么说是极小值而不是最小值，这是因为该问题的损失函数刚好是一个凸函数，在下一小节中，我们会遇到一个非凸函数。

2.4 回到问题

让我们回到原来那条损失函数，在上一小节中，我们对损失函数做了一个简化，在这一小节中，我们要讨论那个没有被简化的损失函数。

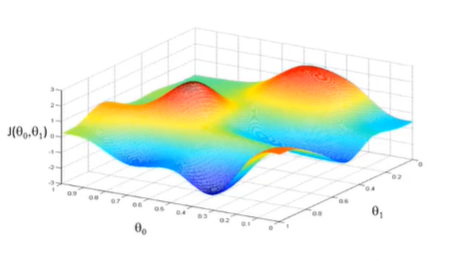
我们初始化${\theta }_0和{\theta }_1$。我们可以设定${\theta }_0=50,{\theta }_1=0.06$，那么可以得到我们第一条直线；而在损失函数中，由于上一小节我们使用的是简化版的损失函数，这也就导致了当时是一个二维的情形，现在引入两个参数，那么这个问题就会上升到三维：

我们的任务就是，找出这个长得像碗的函数的最低点，然后得到它的$({\theta }_0,{\theta }_1)$坐标，然后带回线性回归函数模型中，得到具体的函数，所得的函数即为对训练集拟合最好的函数。

2.5 梯度下降

我们前面定义的代价函数J，但是我们没说怎么让代价降低。我知道你现在肯定有些问题想要知道，以为自己学漏了什么，别担心，下面我就会告诉你学漏了什么。

我们接下来要一种算法，它可以让我们的参数缓慢的接近代价函数图像的极小值点。这种算法不仅被用在线性回归上，还被广泛用于机器学习的各种领域。

梯度下降我们可以分为以下的几个步骤：

我们要做的第一件事就是先给定${\theta }_0和{\theta }_1$的初始值。当然，通常我们初始值为(0,0)。

第二件事就是，我们会通过梯度下降算法不停地一点点改变${\theta }_0和{\theta }_1$。使得$J({\theta }_0,{\theta }_1)$变小，直到我们找到J的最小值。

让我们来看看在图像上梯度下降的工作原理吧。如下是一个非凸损失函数，这样的话我们实际上不知道哪个是最小值，只能知道极小值。

我们要做的就是，站在我们初始化的点所在的位置，然后朝四周看，我们应该走那个方向可以下山，然后朝那个方向迈出既定的一步；然后停下看往四周，重复上述的步骤，直到到达一个自己认为是最低点的位置。

我们来看一下梯度下降算法的数学表示形式吧，实际上，梯度下降的公式是：KaTeX parse error: Undefined control sequence: \part at position 26: …- \alpha \frac{\̲p̲a̲r̲t̲}{\part θ_j} J(…，我们可以这么理解这个公式：当我们发现损失，就往减少损失的方向走去，不断更新自身的位置，直到满意为止，而减少损失的方向在数学上我们叫做梯度，也许这个名词我换个说法更合适，它实际上就是微积分中的偏导，偏导的前面有一个$\alpha$符号，其代表我们应该往损失的方向迈一个多大的步子，我们把这个参数叫做学习率。

2.6 梯度下降知识点总结

让我们对上一小节学过的知识进行一个总结吧。上一小节中，我们学到了梯度下降公式，其中$\alpha$称为学习率，其控制我们以多大的幅度去更新这个参数${\theta }_j$。而$\alpha$后面的那一串我们叫做梯度（偏导）。

实际上对于学习率来说，其控制非常难。我们无法确定好一个合适的学习率。如果学习率过大，可能导致步子过大而错过损失函数的最低点；而如果学习率过小，可能导致步子过小而迭代速度缓慢。所以一般来说根据前人的经验我们可以选几个特定的值。也可以用自适应学习率算法(AdaGrad)动态地在迭代过程中不断更新学习率。

2.7 线性回归模型的梯度下降

我们上面学过的几个函数和算法如下所示：

我们使用梯度下降来处理损失函数时，时常会陷入局部最优。而对于线性回归的损失函数来说，其损失函数往往是一个凸函数，不会有这类担忧。

如果学过线性代数的同学可能知道一种解法，其可以直接解出损失函数的最低点，而不是像梯度下降一般一步一步迭代直至最低点，在后面我们也会详细介绍，这种方法叫正规方程，请不必担心。