致谢

如何理解无偏估计？无偏估计有什么用？什么是无偏估计？_@司南牧|知乎|博客|易懂教程|李韬-CSDN博客_无偏估计

无偏估计【统计学-通俗解释】_guomutian911的专栏-CSDN博客_自由度和无偏估计

8 随机森林

随机森林也叫决策森林。

在下面的小节中，我们会引入一个例子，来看看什么是随机森林，以及决策树为什么会过拟合。

8.1 引入

假如有一个男人，15岁到25岁之间，住在美国，有安卓手机，还在学校读书。喜欢网球和披萨，但不喜欢长时间在沙滩上长散步，那么他很可能下载pokemon go这个软件。

这种做法很不理想，看起来像是在记忆数据，这种情况称为过拟合。决策树经常会过拟合，如果我们选用连续特征也会出现这种问题。决策树有许多节点，它最终会呈现给我们很多个几乎用点相接的小方块。

换而言之，如果不设置特征信息增益的下限，则可能会使得每个叶子都只有一个样本点，从而划分地太细。即一个样本就是一类。

像下图如此，这种分法一般对数据不具备普适性。

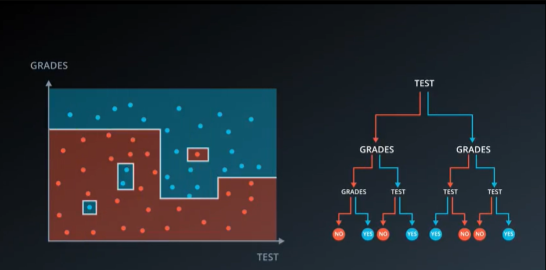
那我们应该如何解决这类问题呢？

我们可以随机从数据中挑选几列，并且根据这些列来构建决策树，就这样我们能构建很多决策树，当我们有一个新的预测时，我们就只需让所有的决策树做出预测，并且选取结果中显示最多的即可，这种方法称为决策森林。

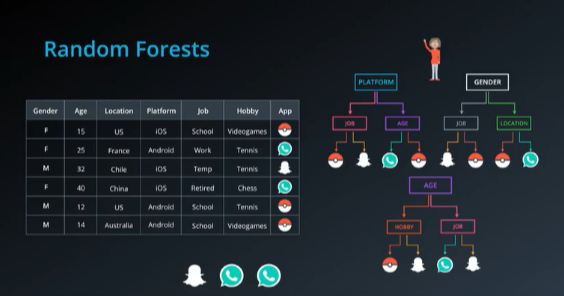
8.2 决策森林

8.2.1 集成学习方法

如果你不是很能听懂我上面的话，没关系，在下面有更多能让你听懂的例子。而在讲述随机森林之前，我们需要先知道什么是集成学习方法。

集成学习方法是通过建立几个模型组合的来解决单一预测问题，它的工作原理是生成多个分类器/模型，各自独立地学习和做出预测。这些预测最后结合成组合预测，因此优于任何一个单分类的做出预测。如同我们上面8.1小节所说，明显地，随机森林就是一种集成学习方法。

集成学习方法大多数分为两种，bagging和boosting。对了，bagging和包包没有关系，它指的是自动聚集。

假设我们现在要做一个测试。我们要做判断题，但是对于做完的选择题答案我们不是很确定，为此，我们找来了许多伙伴；我们从诸多伙伴中一个一个轮流来做这一份选择题。当所有的小伙伴做完这份选择题后，我们把所有的答案集成起来。

如何集成这些答案是一个问题。我们可以采取把所有答案列出来，对于某些题目，有些小伙伴选择对有些小伙伴选择错误。我们比对所有的小伙伴，看看是对的多还是错的多，谁多选谁。这样的话，就类似于雅典城邦的投票选举，我们集各家之长做的题目答案准确率肯定比自己一个人埋头苦干要高得多。

boosting实际上也是在做这么一件事，不过，它会进一步地汲取朋友们的智慧。

假如这份判断题中有很多类型的题目，有政治的有科学的。那么其会从你的小伙伴们挑选出对特定知识了解的相关人物，由它们来解决特定的题目准确率可以进一步提高。

在以上的例子中，我们单个小伙伴叫做弱学习器，而把小伙伴们叫做强学习器。当然弱学习器并不是真的弱，只是相对于强学习器来说的罢了。

8.2.2 什么是随机森林

在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

如下图所示：假如你将一个训练集随机选取五份，即训练了五个决策树分类器，其中四个决策树分类器结果为true，一个决策树分类器结果为false，那么则取大多数人同意的那个结果，即true。

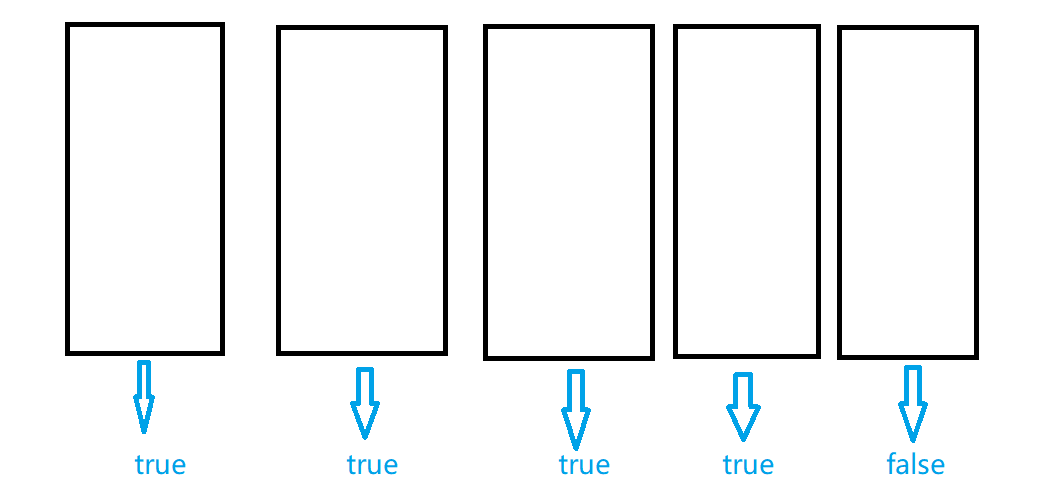
但是其实还有比随机选取列更好的方法。比如说剪枝。但是我们在这一小节暂时先不讲，后面我如果不懒就会提到。

8.2.3 无偏估计

在继续下面的讲解中，我们需要先谈谈无偏估计。而无偏估计与之相对的就是有偏估计。顾名思义，无偏估计就是没有偏差的估计。我们引入一个例子：

假如现在我们要从全市的小学统计出所有小学生数学成绩的平均值。你想想，全市的小学生啊，这是多么庞大的数量，在统计学中，不能全部统计的我们通常会采用抽样统计。即抽取少部分样本，以少部分样本的结果来代替全局结果。

试想，如果你从全市的小学生中随机抽取50个小学生，然后统计50个小学生的平均值。明显地，这具有随机性，用来代替全局结果并不过分，但是明显地，全局结果肯定不会和局部结果相等，这和你抽取的手气有关，说不定你抽到的刚好就是全市学习最差的那几个小学生呢。

上述的过程中实际上出现一个问题。我们每次抽取一个小学生的成绩后是否放回总样本中。如果放回，则说明你的局部样本平均数是总体样本平均数的无偏估计。因为你采用这种方法估算，估算的期望值并没有系统上的误差，无偏估计的误差来源于随机因素；但是，如果你采取不放回，这说明当你抽取多个样本时，如果恰好被你抽走了一些差的，那么剩下的那些肯定是好的，你计算这样的局部概率有意思吗？这样的概率能拿来代替全局概率吗？

8.2.4 决策森林原理过程

在8.2.2中我们提到了随机，那么随机到底怎么个随机法？在决策森林中，我们通常采用BootStrap抽样(随机有放回抽样)，如8.2.3所说，我们之所以选择这种抽样，是为了保持局部决策树的无偏估计性，保证每个决策树做出的决策都是公平的，而不会出现有偏。

在随机森林随机时，对于训练集，我们要保证做到BootStrap抽象。对于特征，我们要从M个特征中随机抽取m个特征，且M>>m，这样的好处是可以起到降维的效果。

8.2.5 决策森林算法实现

说完上述原理，我们来看一下如何实现随机森林。

sklearn.ensemble.RandomForestClassifier(n_estimators = 10,criterion = ‘gini’,max_depth = None,bootstrap = True,random_state = None,min_samples_split = 2)

随机森林分类器
n_estimators：整数类型，指森林里的树木数量，默认为10。通常为120,200,300,500,800,1200。
criterion：字符串类型，默认基尼系数’gini’，你也可以换成熵。
max_depth：整数类型，默认None，用于指定树的最大深度。通常为5,8,15,25,30。
max_features ：字符串类型，每个决策树的最大特征数量，有’auto’,‘sqrt’,‘log2’,'None’四种选择。
bootstrap：布尔类型，默认开启，指是否在构建森林时使用返回抽样
min_samples_split：结点划分最少样本数
min_samples_leaf：叶子结点的最小样本数。
其中n_estimator,max_depth,min_samples_split,min_samples_leaf可以使用超参数网格搜索进行调参。

下面让我们那鸢尾花开刀试一下。

# 导入模块
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCVdef decision_iris():"""随机森林算法"""# 1 获取数据集iris = load_iris()x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=4)# 2 预估器实例化estimator = RandomForestClassifier(criterion="entropy")# 3 指定超参数集合param_dict = {"n_estimators": [120, 200, 300, 500, 800, 1200], "max_depth": [5, 8, 15, 25, 30]}# 4 加入超参数网格搜索和交叉验证estimator = GridSearchCV(estimator, param_grid=param_dict, cv=10)# 5 训练数据集estimator.fit(x_train, y_train)# 6 模型评估y_predict = estimator.predict(x_test)print("y_predict:\n", y_predict)print("直接对比真实值和预测值：\n", y_test == y_predict)score = estimator.score(x_test, y_test)print("准确率为：\n", score)decision_iris()