线性代数(二)

2 解线性方程组

1 Ax = b的列图像实质是A的列向量有各种线性组合，b为其中的一种组合结果。

2 Ax = b可以写为 $Ax = x_1a_1+...+x_na_n = b$ ，其中 $a_1,a_2...a_n$ 为A中的列向量。

3 当Ax = 0时，x有一个取值方式为0向量。

4 若A中有三条列向量，任意一条向量可以由另外两条向量所表示时，我们说该矩阵为奇异矩阵。

5 列图像可以用于解决矩阵乘法

在这一讲中，我们着重要谈论的是关于解方程组的问题。我们先来看下面这样一组等式。

两个方程两个未知数
$0\\ -x+2y = 3$

我们想要解这个方程组，如果按照高中学过的知识，我们会将其直接消元或变量代换，解出其方程。

通过简单的计算，我们很容易得到问题的解：x = 1,y = 2。

实际上，我们可以用矩阵的形式来表示上面的方程组。如我们把方程组中未知数的系数全部提取，然后用一个中括号括起，就可以得到一个系数矩阵。
$[2−1−12]\left[\begin{array}{cc} 2 & -1 \\ -1 & 2 \end{array}\right]$
故我们实际上可以把上面的方程组表示为：
$[2−1−12][xy]=[03]\left[\begin{array}{cc} 2 & -1 \\ -1 & 2 \end{array}\right] \left[\begin{array}{cc} x \\ y \end{array}\right] = \left[\begin{array}{cc} 0 \\ 3 \end{array}\right]$
我们可以将上面的形式进一步简化，看做是Ax = b。

2.1 行图像

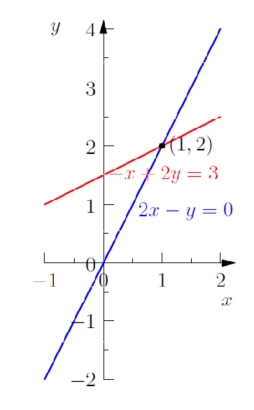
行图像(row picture)为行视角下的图像。我们把一条方程看做一条直线，那么在二维直角坐标系中我们可以轻松地画出方程组的图像。

我们可以很快画出以上的图像，这是一个学生应有的基本素养。

从图像上我们可以看到，对于两方程来说，其解即为行视角下两条直线的交点，即(1,2)为两方程的解。

2.2 列图像

让我们以列图像(column picture)的方式思考一次。

我们可以将上述的方程按照列向量的形式来写出。
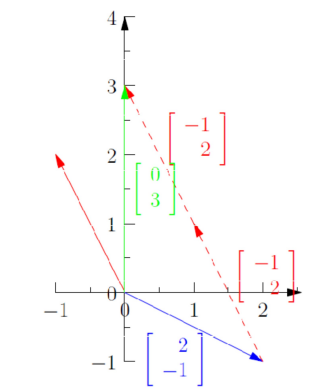
$x[2−1]+y[−12]=[03]x\left[\begin{array}{cc} 2 \\-1 \end{array}\right]+y\left[\begin{array}{cc} -1 \\2 \end{array}\right] = \left[\begin{array}{cc} 0 \\3 \end{array}\right]$
从上面的形式来看，不难看出我们把解方程的问题转为求合适的x、y，使得上述线性组合满足等式。上面的形式我们也能很简单地看出解，我们只需要取一份的列向量1和两份的列向量2即可构造出b。

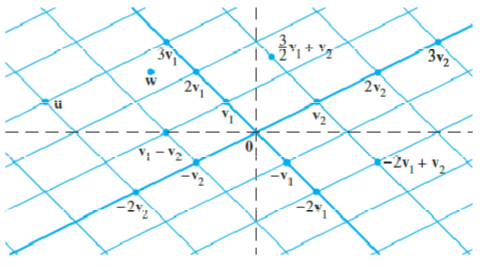
让我们试着以向量的形式将上述的列视角观点画于图像之中。

从图像上看也能验证我们上述的观点。

我们不妨想象。在列图像中，如果col1和col2分别为A中的两条列向量，且它们不共线，那么对于整个平面直角坐标系上的任意一条向量，都可以用col1和col2表示。

换而言之，对于 $x[2−1]+y[−12]x\left[\begin{array}{cc} 2 \\-1 \end{array}\right]+y\left[\begin{array}{cc} -1 \\2 \end{array}\right]$ 来说，由于x，y可任取，故对于平面直角坐标系来说任何一条向量都可以由这两条列向量的线性组合表示。

2.3 三维情况

我们不妨将上述的二维情况推至三维。

三个方程三个未知数
$6\\ 2x+5y+2z = 4\\ 6x-3y+z = 2$

xyz三个未知数可以是不存在的，但是对于本例来说它是存在的。

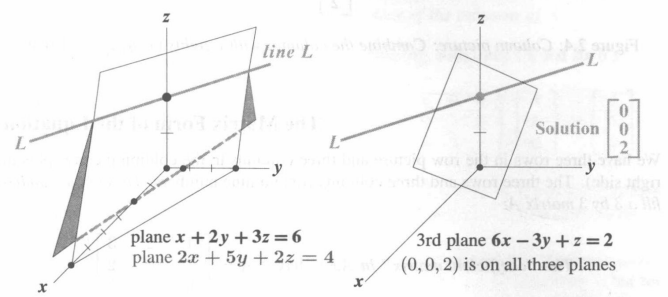
同样地，我们可以将画出上面的行图像。

从图像上不难看出，我们在高维度时最好不要往行视角的方向考虑，因为行图像很难画。

我们不妨从列视角的角度去考虑上面的方程组。
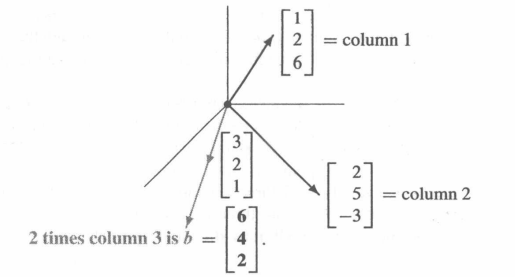
$x[126]+y[25−3]+z[321]=[642]x\left[\begin{array}{cc} 1 \\2\\6 \end{array}\right]+y\left[\begin{array}{cc} 2 \\5\\-3 \end{array}\right]+z\left[\begin{array}{cc} 3\\2\\1 \end{array}\right] = \left[\begin{array}{cc} 6\\4\\2 \end{array}\right]$
同样地，我们在列图像上画出上面的列向量。

通过计算，我们可以知道(x,y,z) = (0,0,2)。

2.4 奇异

我们来思考这样一个问题，当处于三维情况时，我们有Ax = b。那么对于任意的b，是否都能求解Ax = b？

或许我们可以换种问法，对于上述列向量的线性组合，是否能覆盖着整个线性空间。

答案明显是否定的，假如有三条列向量col1,col2,col3。且三条向量均处于同一个平面，此时对于Ax来说，无论如何组合，其得出的新向量都只会在三条列向量所处的平面中，而不会逃离平面。我们把这种情况称为奇异，而把Ax对应的系数矩阵A称为奇异矩阵。

奇异矩阵的研究有多种特殊情况，故在最开始时，我们先暂时不关注奇异问题。

2.5 等式的矩阵形式

我们前面谈论过方程组可以写为矩阵形式。
$[2−1−12][xy]=[03]\left[\begin{array}{cc} 2 & -1 \\ -1 & 2 \end{array}\right] \left[\begin{array}{cc} x \\ y \end{array}\right] = \left[\begin{array}{cc} 0 \\ 3 \end{array}\right]$
那么请问，这个矩阵怎么做乘法呢？

在后面的章节中，我们会提供多种方法供矩阵相乘，现在让我们先用几个老方法来解决这个问题。

2.5.1 点积

我们可以采取点积的形式来完成矩阵的乘法，演示如下：
$[2513][12]=[2×1+5×21×1+3×2]=[127]\left[\begin{array}{cc} 2 & 5 \\ 1 & 3 \end{array}\right] \left[\begin{array}{cc} 1 \\ 2 \end{array}\right] = \left[\begin{array}{cc} 2×1+5×2 \\ 1×1+3×2 \end{array}\right] = \left[\begin{array}{cc} 12\\7 \end{array}\right]$

2.5.2 转换为列图像处理

我们可以可以把矩阵相乘用列视角的观点来看待，演示如下。
$[2513][12]=1[21]+2[53]=[21]+[106]=[127]\left[\begin{array}{cc} 2 & 5 \\ 1 & 3 \end{array}\right] \left[\begin{array}{cc} 1 \\ 2 \end{array}\right] = 1\left[\begin{array}{cc} 2\\1 \end{array}\right]+2 \left[\begin{array}{cc} 5 \\ 3 \end{array}\right] = \left[\begin{array}{cc} 2 \\ 1 \end{array}\right]+\left[\begin{array}{cc} 10 \\ 6 \end{array}\right] = \left[\begin{array}{cc} 12 \\ 7 \end{array}\right]$
这种方式简洁，而且计算不复杂，相对于传统点积形式，我们更应该学会第二种方式来解决矩阵的乘法问题。