傅里叶变换与大数乘法

我们知道，两个 N 位数字的整数的乘法，如果使用常规的算法，时间复杂度是 O(N²)。然而，使用快速傅里叶变换，时间复杂度可以降低到 O(N logN loglogN)。

假设我们要计算以下两个 N 位数字的乘积：

a = (a_N-1a_N-2...a₁a₀)₁₀ = a_N-1x10^N-1 + a_N-2x10^N-2 + ... + a₁x10¹ + a₀x10⁰

b = (b_N-1b_N-2...b₁b₀)₁₀ = b_N-1x10^N-1 + b_N-2x10^N-2 + ... + b₁x10¹ + b₀x10⁰

将上面两个式子相乘，得到以下公式 (共 2N - 1 项)：

c = a x b = c_2N-2x10^2N-2 + c_2N-3x10^2N-3 + ... + c₁x10¹ + c₀x10⁰

非常容易验证，上式中的 c_k ( 0 ≤ k ≤ 2N-2 ) 满足以下公式：

c_k = a₀xb_k + a₁xb_k-1 + ... + a_k-2xb₂ + a_k-1xb₁
+ a_kxb₀ + a_k+1xb_-1 + ... + a_N-2xb_-(N-2-k) + a_N-1xb_-(N-1-k)

上式共有 N 项，a_i 和 b_j 的下标 i 和 j 满足 i + j = k。若不满足 0 ≤ i, j ≤ N-1 时，则令 a_i = b_j = 0。

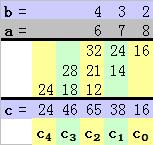
我们以两个 3 ( N = 3 ) 位数 a = 678 和 b = 432 的乘积来说明以上过程吧。

a = (678)₁₀ = 6x10² + 7x10¹ + 8x10⁰

b = (432)₁₀ = 4x10² + 3x10¹ + 2x10⁰

由此：

c₀ = a₀xb₀ + a₁xb_-1 + a₂xb_-2 = 8x2 + 7x0 + 6x0 = 16 + 0 + 0 = 16

c₁ = a₀xb₁ + a₁xb₀ + a₂xb_-1 = 8x3 + 7x2 + 6x0 = 24 + 14 + 0 = 38

c₂ = a₀xb₂ + a₁xb₁ + a₂xb₀ = 8x4 + 7x3 +6x2 = 32 + 21 + 12 = 65

c₃ = a₀xb₃ + a₁xb₂ + a₂xb₁ = 8x0 + 7x4 + 6x3 = 0 + 28 + 18 = 46

c₄ = a₀xb₄ + a₁xb₃ + a₂xb₂ = 8x0 + 7x0 + 6x4 = 0 + 0 + 24 = 24

最后：

c = a x b = 10⁴xc₄ + 10³xc₃ + 10²xc₂ + 10¹xc₁ + 10⁰xc₀
= 10000x24 + 1000x46 + 100x65 + 10x38 + 1x16
= 292896

如果按以上方法计算大整数的乘法，时间复杂度是 O(N²)。

但是，我们注意到，向量 {c_k} 是向量 {a_i} 和向量 {b_j} 的卷积。根据卷积定理，向量卷积的离散傅里叶变换是向量离散傅里叶变换的乘积。于是，我们可以按照以下步骤来计算大整数乘法：

分别求出向量 {a_i} 和向量 {b_j} 的离散傅里叶变换 {A_i} 和 {B_j}。
将 {A_i} 和 {B_j} 逐项相乘得到向量 {C_k}。
对 {C_k} 求离散傅里叶逆变换，得到的向量 {c_k} 就是向量 {a_i} 和向量 {b_j} 的卷积。
对的向量 {c_k} 进行适当的进位就得到了大整数 a 和 b 的乘积 c。

对于复数向量 { x_N-1, ..., x₁, x₀ }，离散傅里叶变换公式为：

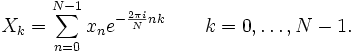
离散傅里叶逆变换公式为：

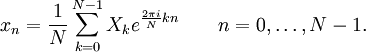
注意到离散傅里叶逆变换除了指数的符号相反以及结果需要乘以归一化因子 1/N 外，与离散傅里叶变换是相同的。所以计算离散傅里叶变换的程序稍做修改也可以用于计算逆变换。

在我们的例子中，乘积 c = 292896，共 6 位数字，N 需要扩展到 2³ = 8。那么，向量 {a_i} 和向量 {b_j} 如下所示：

{ a₇, a₆, a₅, a₄, a₃, a₂, a₁, a₀ } = { 0, 0, 0, 0, 0, 6, 7, 8 }

{ b₇, b₆, b₅, b₄, b₃, b₂, b₁, b₀ } = { 0, 0, 0, 0, 0, 4, 3, 2 }

为了求出以上向量的离散傅里叶变换，我们令

ω = e^-2πi/N = e^-2πi/8 = e^-πi/4 = cos(-π/4) + i sin(-π/4) = √2 / 2 - i √2 / 2 ≈ 0.7-0.7i

为了方便计算，我们预先求出 ω 的各次方，如下：

ω⁸ = ω⁰ = e⁰ = 1

ω⁹ = ω¹ = e^-πi/4 = cos(-π/4) + i sin(-π/4) ≈ 0.7-0.7i

ω¹⁰ = ω² = e^-πi/2 = cos(-π/2) + i sin(-π/2) = -i

ω¹¹ = ω³ = e^-3πi/4 = cos(-3π/4) + i sin(-3π/4) ≈ -0.7-0.7i

ω¹² = ω⁴ = e^-πi = cos(-π) + i sin(-π) = -1

ω¹³ = ω⁵ = e^-5πi/4 = cos(-5π/4) + i sin(-5π/4) ≈ -0.7+0.7i

ω¹⁴ = ω⁶ = e^-3πi/2 = cos(-3π/2) + i sin(-3π/2) = i

ω¹⁵ = ω⁷ = e^-7πi/4 = cos(-7π/4) + i sin(-7π/4) ≈ 0.7+0.7i

注意到当 n > 2 时，a_n = 0，于是：

A₀ = a₀xω^0x0 + a₁xω^1x0 + a₂xω^2x0 = 8xω⁰ + 7xω⁰ + 6xω⁰ = 8x1 + 7x1 + 6x1 = 21

A₁ = a₀xω^0x1 + a₁xω^1x1 + a₂xω^2x1 = 8xω⁰ + 7xω¹ + 6xω² ≈ 8x1 + 7x(0.7 - 0.7i) + 6x(-i) = 12.9-10.9i

A₂ = a₀xω^0x2 + a₁xω^1x2 + a₂xω^2x2 = 8xω⁰ + 7xω² + 6xω⁴ = 8x1 + 7x(-i) + 6x(-1) = 2-7i

A₃ = a₀xω^0x3 + a₁xω^1x3 + a₂xω^2x3 = 8xω⁰ + 7xω³ + 6xω⁶ ≈ 8x1 + 7x(-0.7 - 0.7i) + 6xi = 3.1+1.1i

A₄ = a₀xω^0x4 + a₁xω^1x4 + a₂xω^2x4 = 8xω⁰ + 7xω⁴ + 6xω⁸ = 8x1 + 7x(-1) + 6x1 = 7

A₅ = a₀xω^0x5 + a₁xω^1x5 + a₂xω^2x5 = 8xω⁰ + 7xω⁵ + 6xω¹⁰ ≈ 8x1 + 7x(-0.7 + 0.7i) + 6x(-i) = 3.1-1.1i

A₆ = a₀xω^0x6 + a₁xω^1x6 + a₂xω^2x6 = 8xω⁰ + 7xω⁶ + 6xω¹² = 8x1 + 7xi + 6x(-1) = 2+7i

A₇ = a₀xω^0x7 + a₁xω^1x7 + a₂xω^2x7 = 8xω⁰ + 7xω⁷ + 6xω¹⁴ ≈ 8x1 + 7x(0.7 + 0.7i) + 6xi = 12.9+10.9i

同样，当 n > 2 时，b_n = 0，于是：

B₀ = b₀xω^0x0 + b₁xω^1x0 + b₂xω^2x0 = 2xω⁰ + 3xω⁰ + 4xω⁰ = 2x1 + 3x1 + 4x1 = 9

B₁ = b₀xω^0x1 + b₁xω^1x1 + b₂xω^2x1 = 2xω⁰ + 3xω¹ + 4xω² ≈ 2x1 + 3x(0.7 - 0.7i) + 4x(-i) = 4.1-6.1i

B₂ = b₀xω^0x2 + b₁xω^1x2 + b₂xω^2x2 = 2xω⁰ + 3xω² + 4xω⁴ = 2x1 + 3x(-i) + 4x(-1) = -2-3i

B₃ = b₀xω^0x3 + b₁xω^1x3 + b₂xω^2x3 = 2xω⁰ + 3xω³ + 4xω⁶ ≈ 2x1 + 3x(-0.7 - 0.7i) + 4xi = -0.1+1.9i

B₄ = b₀xω^0x4 + b₁xω^1x4 + b₂xω^2x4 = 2xω⁰ + 3xω⁴ + 4xω⁸ = 2x1 + 3x(-1) + 4x1 = 3

B₅ = b₀xω^0x5 + b₁xω^1x5 + b₂xω^2x5 = 2xω⁰ + 3xω⁵ + 4xω¹⁰ ≈ 2x1 + 3x(-0.7 + 0.7i) + 4x(-i) = -0.1-1.9i

B₆ = b₀xω^0x6 + b₁xω^1x6 + b₂xω^2x6 = 2xω⁰ + 3xω⁶ + 4xω¹² = 2x1 + 3xi + 4x(-1) = -2+3i

B₇ = b₀xω^0x7 + b₁xω^1x7 + b₂xω^2x7 = 2xω⁰ + 3xω⁷ + 4xω¹⁴ ≈ 2x1 + 3x(0.7 + 0.7i) + 4xi = 4.1+6.1i

这样，向量 {a_i} 和向量 {b_j} 的离散傅里叶变换 {A_i} 和 {B_j} 如下所示：

{ A₇, A₆, A₅, A₄, A₃, A₂, A₁, A₀ } = { 12.9+10.9i, 2+7i, 3.1-1.1i, 7, 3.1+1.1i, 2-7i, 12.9-10.9i, 21 }

{ B₇, B₆, B₅, B₄, B₃, B₂, B₁, B₀ } = { 4.1+6.1i, -2+3i, -0.1-1.9i, 3, -0.1+1.9i, -2-3i, 4.1-6.1i, 9 }

现在，将她们逐项相乘得到向量 {C_k}，即 { C₇, C₆, C₅, C₄, C₃, C₂, C₁, C₀ }

= { -13.6+123.4i, -25-8i, -2.4-5.8i, 21, -2.4+5.8i, -25+8i, -13.6-123.4i, 189 }

为了求出向量 {C_k} 的离散傅里叶逆变换，我们令

ω = e^2πi/N = e^2πi/8 = e^πi/4 = cos(π/4) + i sin(π/4) = √2 / 2 + i √2 / 2 ≈ 0.7+0.7i

为了方便计算，我们预先求出 ω 的各次方(注意 ω^k+8 = ω^k)，如下：

ω⁰ = e⁰ = 1

ω¹ = e^πi/4 = cos(π/4) + i sin(π/4) ≈ 0.7+0.7i

ω² = e^πi/2 = cos(π/2) + i sin(π/2) = i

ω³ = e^3πi/4 = cos(3π/4) + i sin(3π/4) ≈ -0.7+0.7i

ω⁴ = e^πi = cos(π) + i sin(π) = -1

ω⁵ = e^5πi/4 = cos(5π/4) + i sin(5π/4) ≈ -0.7-0.7i

ω⁶ = e^3πi/2 = cos(3π/2) + i sin(3π/2) = -i

ω⁷ = e^7πi/4 = cos(7π/4) + i sin(7π/4) ≈ 0.7-0.7i

于是：

c₀ = (1/N) x ( C₀xω^0x0 + C₁xω^1x0 + C₂xω^2x0 + C₃xω^3x0
                  + C₄xω^4x0 + C₅xω^5x0 + C₆xω^6x0 + C₇xω^7x0 )
    = (1/8) x ( 189xω⁰ + (-13.6-123.4i)xω⁰ + (-25+8i)xω⁰ + (-2.4+5.8i)xω⁰
                  + 21xω⁰ + (-2.4-5.8i)xω⁰ + (-25-8i)xω⁰ + (-13.6+123.4i)xω⁰ )
    = 0.125 x ( 189x1 + (-13.6-123.4i)x1 + (-25+8i)x1 + (-2.4+5.8i)x1
                  + 21x1 + (-2.4-5.8i)x1 + (-25-8i)x1 + (-13.6+123.4i)x1 )
    = 0.125 x 128 = 16

c₁ = (1/N) x ( 8xc₁ = C₀xω^0x1 + C₁xω^1x1 + C₂xω^2x1 + C₃xω^3x1
                  + C₄xω^4x1 + C₅xω^5x1 + C₆xω^6x1 + C₇xω^7x1 )
    = (1/8) x ( 189xω⁰ + ( -13.6-123.4i)xω¹ + (-25+8i)xω² + (-2.4+5.8i)xω³
                  + 21xω⁴ + (-2.4-5.8i)xω⁵ + (-25-8i)xω⁶ + (-13.6+123.4i)xω⁷ )
    ≈ 0.125 x ( 189x1 + (-13.6-123.4i)x(0.7+0.7i) + (-25+8i)x(i) + (-2.4+5.8i)x(-0.7+0.7i)
                  + 21x(-1) + (-2.4-5.8i)x(-0.7-0.7i) + (-25-8i)x(-i) + (-13.6+123.4i)x(0.7-0.7i) )
    = 0.125 x 300.96 = 37.62 ≈ 38

c₂ = (1/N) x ( C₀xω^0x2 + C₁xω^1x2 + C₂xω^2x2 + C₃xω^3x2
                  + C₄xω^4x2 + C₅xω^5x2 + C₆xω^6x2 + C₇xω^7x2 )
    = (1/8) x ( 189xω⁰ + (-13.6-123.4i)xω² + (-25+8i)xω⁴ + (-2.4+5.8i)xω⁶
                  + 21xω⁸ + (-2.4-5.8i)xω¹⁰ + (-25-8i)xω¹² + (-13.6+123.4i)xω¹⁴ )
    = 0.125 x ( 189x1 + (-13.6-123.4i)x(i) + (-25+8i)x(-1) + (-2.4+5.8i)x(-i)
                  + 21x1 + (-2.4-5.8i)x(i) + (-25-8i)x(-1) + (-13.6+123.4i)x(-i) )
    ≈ 0.125 x 518.4 = 64.8 ≈ 65

c₃ = (1/N) x ( C₀xω^0x3 + C₁xω^1x3 + C₂xω^2x3 + C₃xω^3x3
                  + C₄xω^4x3 + C₅xω^5x3 + C₆xω^6x3 + C₇xω^7x3 )
    = (1/8) x ( 189xω⁰ + (-13.6-123.4i)xω³ + (-25+8i)xω⁶ + (-2.4+5.8i)xω⁹
                  + 21xω¹² + (-2.4-5.8i)xω¹⁵ + (-25-8i)xω¹⁸ + (-13.6+123.4i)xω²¹ )
    ≈ 0.125 x ( 189x1 + (-13.6-123.4i)x(-0.7+0.7i) + (-25+8i)x(-i) + (-2.4+5.8i)x(0.7+0.7i)
                  + 21x(-1) + (-2.4-5.8i)x(0.7-0.7i) + (-25-8i)x(i) + (-13.6+123.4i)x(-0.7-0.7i) )
    = 0.125 x 364.32 = 45.54 ≈ 46

c₄ = (1/N) x ( C₀xω^0x4 + C₁xω^1x4 + C₂xω^2x4 + C₃xω^3x4
                  + C₄xω^4x4 + C₅xω^5x4 + C₆xω^6x4 + C₇xω^7x4 )
    = (1/8) x ( 189xω⁰ + (-13.6-123.4i)xω⁴ + (-25+8i)xω⁸ + (-2.4+5.8i)xω¹²
                  + 21xω¹⁶ + (-2.4-5.8i)xω²⁰ + (-25-8i)xω²⁴ + (-13.6+123.4i)xω²⁸ )
    = 0.125 x ( 189x1 + (-13.6-123.4i)x(-1) + (-25+8i)x1 + (-2.4+5.8i)x(-1)
                  + 21x1 + (-2.4-5.8i)x(-1) + (-25-8i)x1 + (-13.6+123.4i)x(-1) )
    = 0.125 x 192 = 24

c₅ = (1/N) x ( C₀xω^0x5 + C₁xω^1x5 + C₂xω^2x5 + C₃xω^3x5
                  + C₄xω^4x5 + C₅xω^5x5 + C₆xω^6x5 + C₇xω^7x5 )
    = (1/8) x ( 189xω⁰ + (-13.6-123.4i)xω⁵ + (-25+8i)xω¹⁰ + (-2.4+5.8i)xω¹⁵
                  + 21xω²⁰ + (-2.4-5.8i)xω²⁵ + (-25-8i)xω³⁰ + (-13.6+123.4i)xω³⁵ )
    ≈ 0.125 x ( 189x1 + (-13.6-123.4i)x(-0.7-0.7i) + (-25+8i)x(i) + (-2.4+5.8i)x(0.7-0.7i)
                  + 21x(-1) + (-2.4-5.8i)x(0.7+0.7i) + (-25-8i)x(-i) + (-13.6+123.4i)x(-0.7+0.7i) )
    = 0.125 x 3.04 = 0.38 ≈ 0

c₆ = (1/N) x ( C₀xω^0x6 + C₁xω^1x6 + C₂xω^2x6 + C₃xω^3x6
                  + C₄xω^4x6 + C₅xω^5x6 + C₆xω^6x6 + C₇xω^7x6 )
    = (1/8) x ( 189xω⁰ + (-13.6-123.4i)xω⁶ + (-25+8i)xω¹² + (-2.4+5.8i)xω¹⁸
                  + 21xω²⁴ + (-2.4-5.8i)xω³⁰ + (-25-8i)xω³⁶ + (-13.6+123.4i)xω⁴² )
    = 0.125 x ( 189x1 + (-13.6-123.4i)x(-i) + (-25+8i)x(-1) + (-2.4+5.8i)x(i)
                  + 21x1 + (-2.4-5.8i)x(-i) + (-25-8i)x(-1) + (-13.6+123.4i)x(i) )
    = 0.125 x 1.6 = 0.2 ≈ 0

c₇ = (1/N) x ( C₀xω^0x7 + C₁xω^1x7 + C₂xω^2x7 + C₃xω^3x7
                  + C₄xω^4x7 + C₅xω^5x7 + C₆xω^6x7 + C₇xω^7x7 )
    = (1/8) x ( 189xω⁰ + (-13.6-123.4i)xω⁷ + (-25+8i)xω¹⁴ + (-2.4+5.8i)xω²¹
                  + 21xω²⁸ + (-2.4-5.8i)xω³⁵ + (-25-8i)xω⁴² + (-13.6+123.4i)xω⁴⁹ )
    ≈ 0.125 x ( 189x1 + (-13.6-123.4i)x(0.7-0.7i) + (-25+8i)x(-i) + (-2.4+5.8i)x(-0.7-0.7i)
                  + 21x(-1) + (-2.4-5.8i)x(-0.7+0.7i) + (-25-8i)x(i) + (-13.6+123.4i)x(0.7+0.7i) )
    = 0.125 x 3.68 = 0.46 ≈ 0

这样，我们就使用离散傅里叶变换和逆变换计算出了向量 {a_i} 和向量 {b_j} 的卷积向量 {c_k}，如下所示：

{ c₇, c₆, c₅, c₄, c₃, c₂, c₁, c₀ } = { 0, 0, 0, 0, 24, 46, 65, 38, 16 }

这和我们在前面直接使用向量 {a_i} 和向量 {b_j} 来计算卷积的结果是一样的。

但是，这个算法的时间复杂度还是 O(N²)。我们绕了这么一大圈，不是白费劲了吗？

现在就到了关键时刻，关键在于：直接进行离散傅里叶变换的计算复杂度是 O(N²)。快速傅里叶变换可以计算出与直接计算相同的结果，但只需要 O(N logN) 的计算复杂度。 N logN 和 N² 之间的差别是巨大的。例如，当 N = 10⁶ 时，在一个每秒运算百万次的计算机上，粗略地说，它们之间就是占用 30 秒 CPU 时间和两星期 CPU 时间的差别。

快速傅里叶变换的要点如下：一个界长为 N 的离散傅里叶变换可以重新写成两个界长各为 N/2 的离散傅里叶变换之和。其中一个变换由原来 N 个点中的偶数点构成，另一个变换由奇数点构成。这个过程可以递归地进行下去，直到我们将全部数据细分为界长为 1 的变换。什么是界长为 1 的傅里叶变换呢？它正是把一个输入值复制成它的一个输出值的恒等运算。要实现以上算法，最容易的情况是原始的 N 为 2 的整幂次项，如果数据集的界长不是 2 的幂次时，则可添上一些零值，直到 2 的下一幂次。在这个算法中，每递归一次需 N 阶运算，共需要 log N 次递归，所以快速傅里叶变换算法的时间复杂度是 O(N logN)。

由于快速傅里叶变换是采用了浮点运算，因此我们需要足够的精度，以使在出现舍入误差时，结果中每个组成部分的准确整数值仍是可辨认的。长度为 N 的 B 进制数可产生大到 B²N 阶的卷积分量。我们知道，双精度浮点数的尾数是 53 个二进位，所以：

2 x log₂B + log₂N + 几个 x log₂log₂N < 53

上式中左边最后一项是为了快速傅里叶变换的舍入误差。

所以，为了能够计算尽量大的整数，一般 B 不会取得太大。在计算机程序中经常使用 256 进制进行运算。但是如果经常需要将计算结果和十进制互相转换，则往往使用 100 进制进行运算。

关于快速傅里叶变换以及卷积定理的更深入的知识，请参阅文末的参考文献。这一篇随笔主要是讲述相关的原理，在下一篇随笔中，我将给出一个使用快速傅里叶变换进行任意精度的算术运算的 C# 程序。

顺便说一句，我在准备正文的例题的时候，是使用 google 计算器来进行复杂的复数运算的。发现她非常好用。以计算 c₂ 为例，只要将要计算的表达式复制到 goole 搜索栏，然后按回车，就能得到计算结果：

(189 x 1) + (((-13.6) - (123.4 * i)) x i) + (((-25) + (8 * i)) x (-1)) + (((-2.4) + (5.8 * i)) x (-i)) + (21 x 1) + (((-2.4) - (5.8 * i)) x i) + (((-25) - (8 * i)) x (-1)) + (((-13.6) + (123.4 * i)) x (-i)) = 518.4 - 1.77635684 × 10^-15 i
Google 计算器详情

找不到和您的查询 "189x1 + (-13.6-123.4i)x(i) + (-25+8i)x(-1) + (-2.4+5.8i)x(-i) + 21x1 + (-2.4-5.8i)x(i) + (-25-8i)x(-1) + (-13.6+123.4i)x(-i)" 相符的网页。

参考文献：