Humans have plenty of cognitive strengths, but one area that most of us struggle with is estimating, explaining and preparing for improbable events. This theme underpins two of Nassim Taleb’s major works: Fooled by Randomness and The Black Swan: The Impact of the Highly Improbable. In the latter work, Taleb defines a black swan events as having three characteristics: the event is a surprise (to the observer), it has a major effect, and people incorrectly try to rationalize it in hindsight (emphasis mine).

人类具有大量的认知能力，但是我们大多数人都在努力的领域之一是估计，解释和为不可能的事件做准备。 这个主题奠定了纳西姆·塔莱布 ( Nassim Taleb )的两部主要作品的基础： 愚弄随机和《黑天鹅：高度不可能的影响》 。 在后者的工作中，塔莱布将黑天鹅事件定义为具有三个特征：(对观察者而言)该事件是一个意外事件，具有重大影响，并且人们事后错误地尝试将其合理化 (强调我的观点 )。

Taleb focuses on black swan events on the world stage, such as the creation of the internet, World War I, and the dissolution of the Soviet Union. I believe that humans behave similarly, and to their detriment, with less unlikely events predicted by statistical models as long as they’re important. We’ve seen this recently in the results of the 2016 presidential election results. Models published by The Huffington Post, The New York Times, and 538 all had Hillary Clinton at a 71–98% chance of winning. After she lost the election, a common reaction was whether we could trust polls [and the models that rely on their data] again, which I was surprise to see even from statistically minded friends. Why is our gut reaction to scrutinize the model that said Trump had a 29% chance of winning? We wouldn’t question the fairness of a coin that comes up tails twice (25% chance) or a 1 of a rolled die (17% chance); both of which are lower than the odds given to Trump winning the 2016 election.

塔莱布(Taleb)专注于世界舞台上的黑天鹅事件，例如互联网的创建，第一次世界大战和苏联解体。 我相信人类的行为类似，并且对他们有害，只要它们很重要，统计模型就可以预测不太可能发生的事件。 我们最近在2016年总统选举结果中看到了这一点。 《赫芬顿邮报》 ， 《纽约时报》和538发表的模型都以希拉里·克林顿的获胜机率达71–98％。 在她失去选举后，一个普遍的React是我们是否可以再次信任民意测验(以及依赖于他们数据的模型)，即使是从统计学角度看的朋友，我也感到惊讶。 为什么我们的直觉会仔细审查表示特朗普有29％获胜机会的模型？ 我们不会质疑两次出现尾巴的硬币的公平性(25％的机率)或一枚掷骰子的硬币的公平性(17％的机率)； 两者都低于特朗普赢得2016年大选的机会。

I posit that this reaction, which is a form of rationalization by hindsight, is due to the lack of a mental framework to grapple with real world event probabilities, and that not having this framework can result in irrational decision-making. In order to illustrate this, let’s move away from the world of election modeling to a more common situation encountered in the business world.

我认为，这种React是事后回想的一种合理化形式，是由于缺乏解决现实世界事件概率的心理框架，而没有这个框架会导致非理性的决策。 为了说明这一点，让我们从选举建模的世界转移到商业世界中遇到的更常见的情况。

最黑暗的时间表 (The darkest timeline)

Imagine you’re a data scientist who models the probability of closing sales with potential clients at a business-to-business tech company. Your company is in the process of courting a particularly large client, Megacorp, and so the CEO checks your model every day to track the odds of closing the sale.

想象一下，您是一位数据科学家，他对企业对企业技术公司与潜在客户达成销售的可能性进行建模。 您的公司正在寻求一个特别大的客户Megacorp，因此CEO每天都要检查您的模型以跟踪完成交易的几率。

Thursday: 98% of closing sale

星期四 ：收盘价的98％

Incredible news! Whatever your teammates are doing looks like it’s working.

令人难以置信的消息！ 无论您的队友在做什么，都看起来很正常。

Friday: 99% of closing sale

星期五 ：成交价的99％

Even better! The CEO starts planning the changes he’ll need to make to your business after the anticipated windfall. Hire more employees? Acquire a competitor? Buy a superbowl ad?

更好！ 首席执行官开始计划在预期的意外收获后需要对您的业务进行的更改。 雇用更多员工？ 收购竞争对手？ 购买超级碗广告？

Monday: 0% of closing sale

星期一 ：收盘价的0％

What happened?! You learn that the prospective client chose to go with a competitor at the last minute. This is a huge blow to everybody’s morale, and the time and energy the CEO spent dreaming about expansion after the sale he thought was practically guaranteed was wasted.

发生了什么？！ 您了解到，潜在客户在最后一刻选择了与竞争对手同行。 这对每个人的士气都造成了巨大的打击，而CEO认为梦想中的扩张实际上浪费了很多时间和精力。

What’s a common reaction to this fiasco? “The model must be wrong!” the CEO declares during the postmortem meeting he calls with you. “We should have known that this wasn’t as likely as you said it was. I don’t want to hear from you until it’s fixed.”

对这场惨败的普遍React是什么？ “模型一定是错误的！” CEO在事后会议上宣布与您通话。 “我们应该知道，这种可能性不如您所说的那样大。 在解决问题之前，我不希望收到您的来信。”

产生问题 (Creating a problem)

It’s possible that the CEO is correct. Your model could have predicted a lower chance of closing the sale that your company didn’t end up getting. However, it’s also possible that the model is fine. Your company had a very high chance of closing that sale, but the unlikely happened, and you just didn’t get it.

CEO可能是正确的。 您的模型可能会预测完成您的公司最终没有获得的销售的机会较低。 但是，该模型也可能很好。 贵公司有很高的机会完成那笔交易，但是发生的可能性很小，而您却没有得到。

You are now in an uncomfortable position. It’s possible that the only way of “improving” the model, is to produce one that estimates lower odds of closing the Megacorp sale at the expense of modeling future sales accurately. This is called overfitting. By complying with your CEO’s request in order to stay in his good graces, you’re doing damage to your model — and the company — by distorting predictions of future sales.

您现在处于不舒服的位置。 “改善”模型的唯一方法可能是产生一种估计Megacorp销售的较低赔率的方法，而以准确建模未来销售为代价 。 这称为过拟合 。 通过遵守CEO的要求以保持他的良好风度，您正在歪曲对未来销售的预测，从而损害了您的模型以及整个公司。

回归本源 (Back to basics)

Before we get to my proposed mental framework that can help folks better understand complex, real world event probabilities, let’s start with a simple example. Imagine you have a fair six sided die. You roll the die over and over and start recording results. After many rolls, you observe what you’d expect: around the same number of rolls come up with each number, one through six.

在我们提出可以帮助人们更好地理解复杂的，现实世界中的事件概率的心理框架之前，让我们从一个简单的示例开始。 想象您有一个公平的六面模。 您将骰子一遍又一遍地滚动并开始记录结果。 经过多次掷骰后，您会观察到期望的结果：每个号码都会出现相同数目的掷骰，从一到六。

After a few hundred rolls, you get an unlikely, and unlucky (in most games) streak. A 1, followed by another 1, followed by another 1! The odds of this happening are 1/216 = ~0.5%. This is an unlikely event. Are you surprised? Do you doubt the fairness of the die? Do you tell the die it better fix itself before you roll it again?

经过几百次掷骰后，您会获得不太可能的，不幸的(在大多数游戏中)连胜纪录。 一个1，然后是另一个1，然后是另一个1！ 发生这种情况的几率是1/216 =〜0.5％。 这是不太可能发生的事件。 你惊喜吗？ 您是否怀疑死亡的公平性？ 您是否告诉模子在再次滚动之前更好地自我修复？

Most people, even those without any statistical training, would say no. What happened was unlikely, but the die was behaving as expected otherwise. Additionally, if we think hard enough about it, we can explain the mechanism behind the randomness of the die rolls. Once the die leaves your hand, it is subject to the laws of physics, and is entirely predictable. The reason die throws are random is that slight changes in the velocity and orientation immediately after release result in different outcomes. Nobody has the fine motor skills necessary to cheat at die rolling, which would allow them to let some numbers appear more frequently than others.

大多数人，甚至没有经过统计学培训的人也会拒绝。 发生的事情不太可能发生，但是死亡的行为与预期相反。 此外，如果我们认真考虑一下，就可以解释模头辊随机性背后的机理。 一旦模具离开您的手，它就受物理定律的约束，并且完全可以预测。 掷骰子是随机的，原因是释放后立即改变速度和方向会导致不同的结果。 没有人具有在压铸时作弊的必要的高级运动技能，这会使他们让某些数字比其他数字更频繁地出现。

We can use the idea of statistical populations, which are “a set of similar items or events which is of interest for some question or experiment” (Wikipedia). In this case, the items of interest are die rolls. As velocity and orientation vary, we get different outcomes.

我们可以使用统计种群的概念，即“一些问题或实验都感兴趣的一组相似的项目或事件”( 维基百科 )。 在这种情况下，感兴趣的项目是模具卷。 随着速度和方向的变化，我们得到不同的结果。

When we roll the die, what we’re doing is sampling from this population. The population of all possible throws (even the ones where the die drops out of your hand or is hurled out of an open window) contains equal shares of each outcome. If we think of this in terms of area, as is shown in the diagram above, we can imagine that the population has equal areas for each outcome, one through six.

当我们掷骰子时，我们正在做的是从这个总体中采样。 所有可能的掷出的总数(甚至是骰子掉落到您手中或被掷出一个打开的窗口的那些掷出)所包含的每个结果的份额相等。 如上图所示，如果我们以面积为单位来考虑这一点，我们可以想象每个结果中的人口具有相等的面积，从1到6。

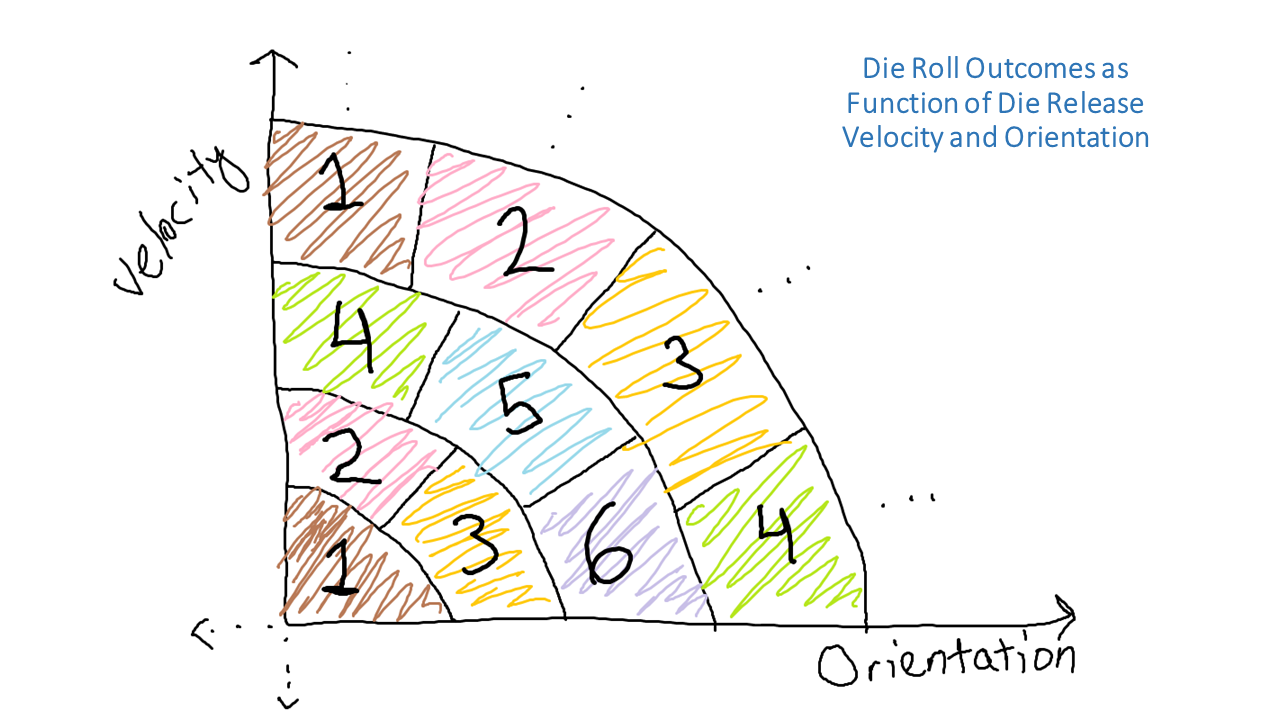
Before we add some complexity, I want to reinforce the idea that although there are only six equally likely die roll outcomes, there are infinite combinations of velocity and orientation, which when obeying the unchanging laws of physics, result in those outcomes. We can imagine doing two distinct types of work with this strong understanding of die rolling:

在我们增加一些复杂性之前，我想强调一下这样的观点：尽管只有六个同样可能的掷骰结果，但速度和方向有无限的组合，当遵循物理不变的定律时，会导致这些结果。 我们可以想象在对压铸有深入了解的情况下进行两种截然不同的工作：

1. We can use our understanding of the equally weighted population outcomes to come up with optimal strategies in different areas such as games, gambling, and business.

   我们可以使用对加权平均结果的理解来提出不同领域(例如游戏，赌博和商业)的最佳策略。

2. We could try to use our understanding of the mechanism driving the equal probabilities, namely that the velocity and orientation of the die after release can perfectly predict its outcome, to try to get certain outcomes to happen more frequently. A human couldn’t do this, but perhaps we could create a robot that can throw a die that results in 6s every time.

   我们可以尝试使用对驱动相等概率的机制的理解，即释放后模具的速度和方向可以完美地预测其结果，从而尝试使某些结果更频繁地发生。 人类无法做到这一点，但是也许我们可以创造一个可以掷出骰子的机器人，每次导致6s的死亡。

增加复杂性 (Adding back complexity)

What’s the statistical population in our sales example? Most folks would answer that it’s all possible sales clients. I’ve always found something frustrating with this definition: we can’t use it to explain why our model returns a 99% chance of landing the sale that we didn’t get without admitting that it must be model error. If that’s the case, our CEO — who is not an expert in probability and statistics— feels justified in his request.

我们的销售示例中的统计人口是多少？ 大多数人会回答这是所有可能的销售客户。 我总是对这个定义感到沮丧：我们不能用它来解释为什么我们的模型在没有承认一定是模型错误的情况下获得了99％的机会获得了我们没有得到的销售。 如果是这样，我们的首席执行官(不是概率和统计专家)会觉得有道理。

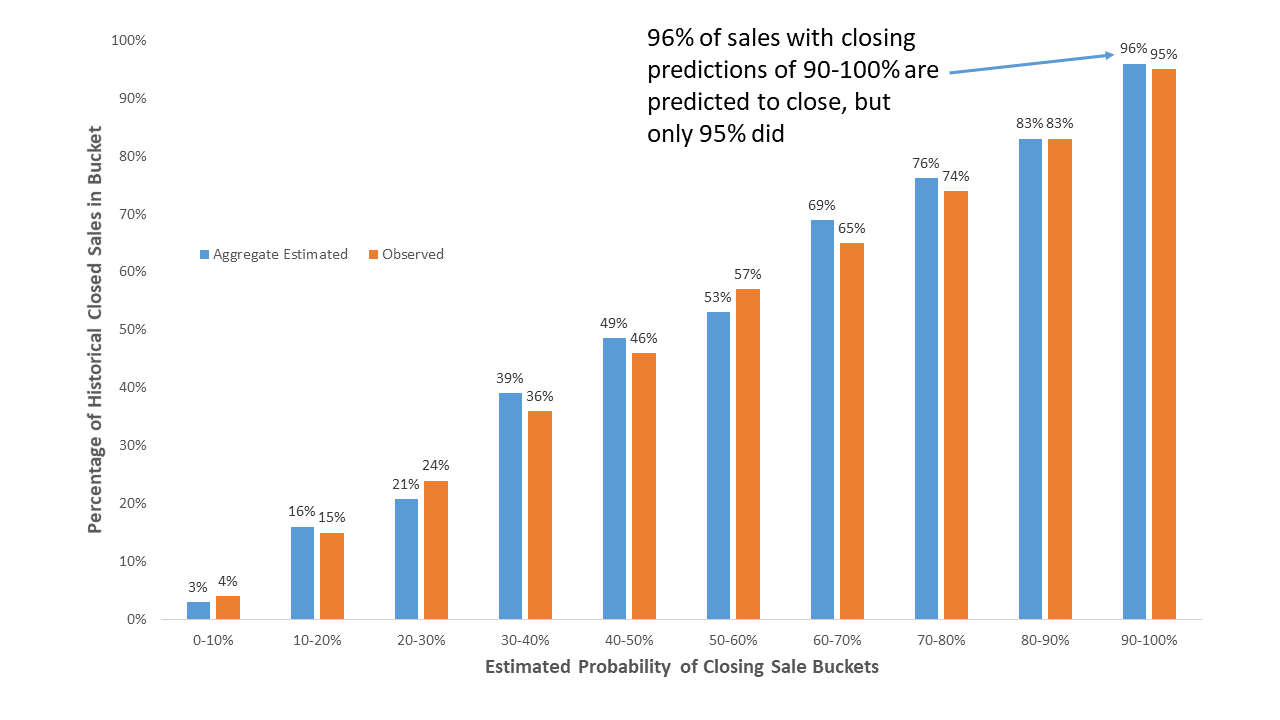
One way we could address this is to group predictions together in accuracy buckets (e.g. 0–10%, 10–20%, … 90–100%) and chart their accuracies jointly. A well performing model will show that these predictions behave around what’s observed in aggregate.

我们可以解决这个问题的一种方法是将预测合并到准确度组中(例如0–10％，10–20％，…90–100％)，并共同绘制其准确性。 表现良好的模型将表明，这些预测与总体观察到的结果一致。

This still doesn’t satisfy my need to understand that predicted 99%. Imagine that in aggregate, we predict 96% of the sales in the 90–100% predicted bucket to be closed, but only 95% are. One could still argue that by fixing the model, and bringing down our predicted 99%, we still improve this aggregate accuracy.

这仍然不能满足我对99％预测值的理解。 想象一下，总体而言，我们预计90-100％的预测存储段中的96％的销售将关闭，但只有95％的交易将关闭。 仍然可以说，通过修复模型并降低我们的预测99％，我们仍然可以提高这一总体准确性。

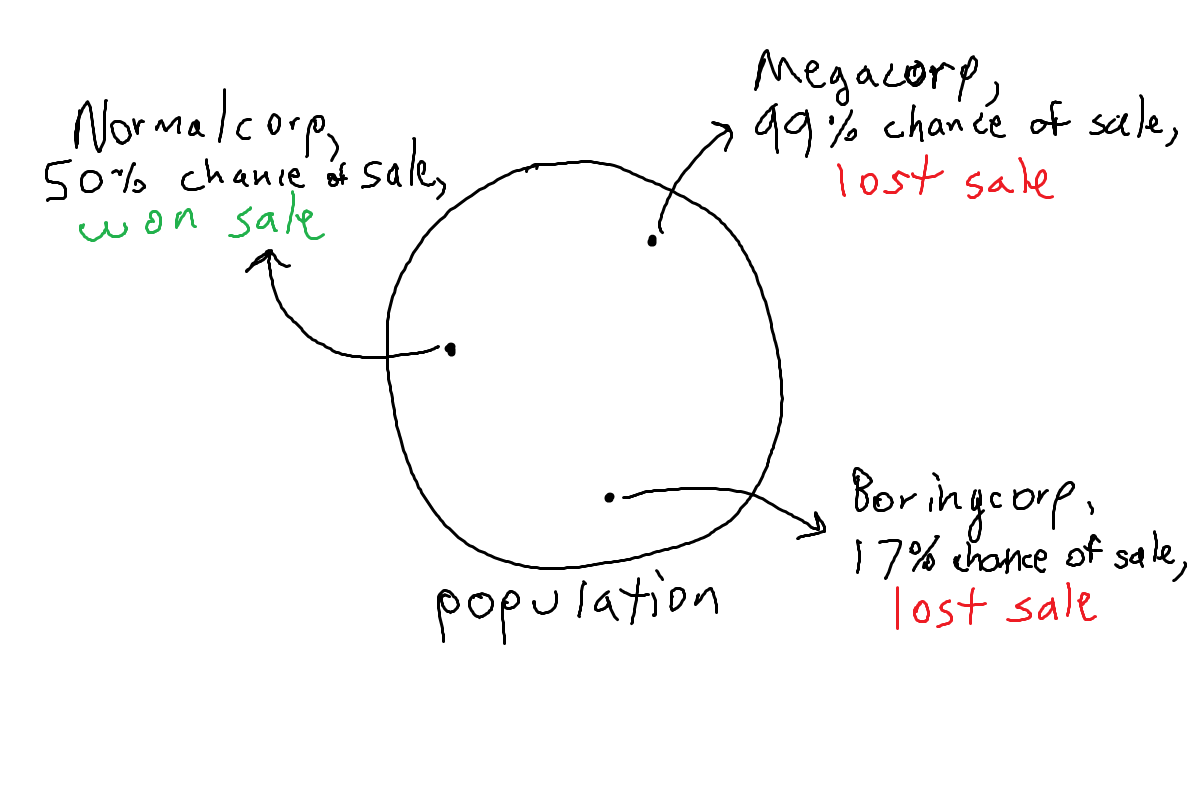
Unlike in the die rolling example, we can’t easily resample from the population. We can’t relive history, pitching Megacorp 100 times in 100 slightly different ways and land that sale 99 out of those 100 times. But we can imagine doing so with multiverse theory! In multiverse theory, specifically Level III: The Many-Worlds Interpretation, all possible outcomes of probabilistic events happen in some universe and do so in proportion to their probabilities. I’d like to define a multiverse population as the statistical populations (in this example: all potential clients) in all possible universes. Expanding upon the statistical population example above, we can turn every dot, which represented each potential client, into a circle which represents that potential client’s outcomes in all universes. The higher the likelihood of winning that client’s business, the greater the proportion of universes in which their business is won, and therefore the larger the area in the client circle. Note that if I shaded in the entire multiverse population, it would resemble the die rolling diagram I shared earlier.

与模版滚动示例不同，我们无法轻松地从总体中重新采样。 我们无法重温历史，以100种略有不同的方式向Megacorp推销100次，并在这100次中售出99次。 但是我们可以想象用多元宇宙理论来做到这一点！ 在多元宇宙理论中 ，特别是在第III层级：“多世界解释”中 ，概率事件的所有可能结果都发生在某个宇宙中，并且与它们的概率成比例地发生。 我想将多宇宙人口定义为所有可能宇宙中的统计人口(在本例中为所有潜在客户) 。 扩展上面的统计总体示例，我们可以将代表每个潜在客户的每个点变成一个圆圈，该圆圈代表所有宇宙中该潜在客户的结果。 赢得该客户的业务的可能性越高，赢得其业务的Universe的比例就越大，因此客户圈子的面积越大。 请注意，如果我在整个多宇宙总体中进行阴影处理，则它将类似于我之前共享的模具滚动图。

拥有多元宇宙心理框架的好处 (Benefits of having a multiverse mental framework)

Astute readers have noticed that we cannot use this multiverse approach to probabilities to prove that our model is correct. We can’t hop from universe to universe, tabulating the proportion in which we win the Megacorp sale to show our CEO that our model is working as intended. In fact, it’s impossible to show that any model perfectly explains the world. The best we can do is to know that a model reasonably predicts samples from our population of interest, often by contrasting it with other, less accurate models. Even then, we still rely on assumptions to do so, one of the most important of which is that the systems does not undergo unanticipated structural changes. All of our predictions will be off if such a change happens. In our example, a strong competitor entering or leaving the market would represent such a change.

精明的读者已经注意到，我们不能使用这种多元方法来证明我们的模型是正确的。 我们无法在宇宙之间跳来跳去，列出赢得Megacorp交易的比例以向我们的CEO展示我们的模型正在按预期工作。 实际上，不可能显示出任何模型都能完美地解释世界。 我们能做的最好的事情就是知道一个模型可以合理地从我们感兴趣的人群中预测样本，通常是将其与其他不太准确的模型进行对比。 即使到那时，我们仍然要依靠假设来做到这一点，其中最重要的一项是系统不会发生意外的结构变化。 如果发生这种变化，我们所有的预测都将失效。 在我们的示例中，强大的竞争者进入或退出市场将代表这种变化。

In my experience, many data scientists ignore or even dismiss non-empiric ideas such as this multiverse theory approach to grappling with probabilities, but they are doing so at their own peril. The first benefit of using the theory is that it is an accessible way of explaining probabilities to those who don’t have a strong background in them, like the CEO in our example. It’s possible that explaining your model outputs using multiverse theory helps consumers of your models become more comfortable with how to interpret them. It can be done on its own or addition to a short explanation on overfitting to persuade our hypothetical CEO to drop his (potentially) irrational demand to tweak your model until it brings down the Megacorp sale probability.

以我的经验，许多数据科学家会忽略甚至忽略非经验性的想法，例如这种采用多元理论来解决概率问题的方法，但这样做的后果自负。 使用该理论的第一个好处是，它是一种向那些没有较深背景的人(例如我们的示例中的CEO)解释概率的一种可访问的方法。 使用多元宇宙理论解释模型的输出可能会帮助模型的使用者对如何解释它们感到更自在。 它可以单独完成，也可以在简短说明中补充说服力，以说服我们假设的首席执行官放弃(可能)不合理的需求来调整您的模型，直到降低Megacorp的销售概率。

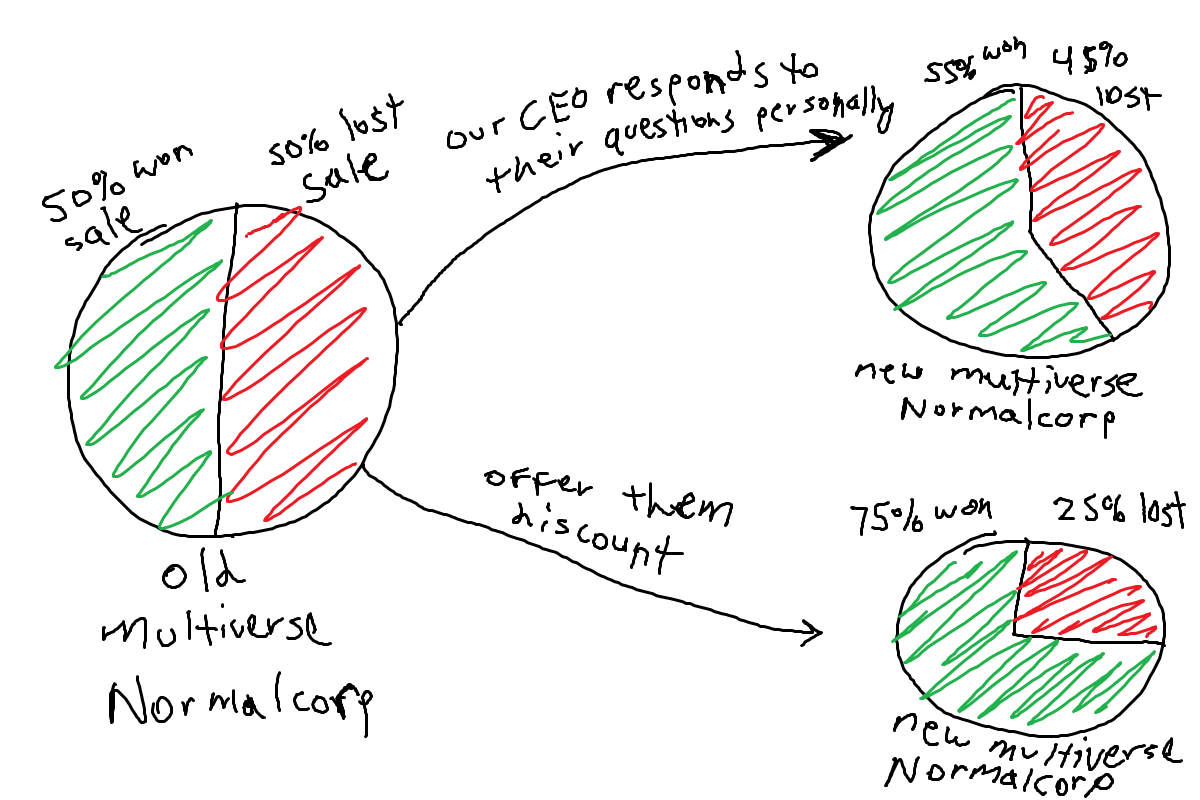
The second benefit is that the multiverse theory approach to interpreting probabilities is that it gives us a useful structure for what-if analyses. Remember the mechanism for randomness in our die rolling example? I shared that the reason a fair die comes up with each outcome in the same proportion is because small changes — smaller than we can control with our fine motor skills — result in different outcomes. We can show that using a little more force or a different orientation turns a throw that would result in a 1 into one that results in a 2. Unfortunately, business outcomes cannot be predicted perfectly by a system as consistent as classical mechanics. However, we can try to imagine what we could have done differently to increase our chances of closing the Megacorp sale and use it to help with future ones. People do this all the time when they do what-if analyses: one can imagine the CEO thinking “if only I had answered Megacorp’s questions about our service personally” or “I wonder what would have happened if we gave them a discount because they’d be an impressive client to have.” We need to understand that neither of these actions guarantees the sale, but they can increase its odds, and applying the multiverse theory we can imagine flipping universes in which the sale is not made to ones in which it is. In the below diagram, I demonstrate what this would look like for the Normalcorp client, which originally has a 50% chance of sale, as increases from 50% are easier to see.

第二个好处是，用于解释概率的多元宇宙理论方法为我们提供了一种假设分析的有用结构。 还记得我们的掷骰示例中的随机性机制吗？ 我分享了每个结果以相同比例出现的原因是因为微小的变化(小于我们可以用自己的精细运动技能控制的变化)导致不同的结果。 我们可以证明，使用更多的力或使用不同的方向可以将导致1的掷变成2的掷。不幸的是，系统无法像传统力学一样完美地预测业务结果。 但是，我们可以尝试想象我们可以做些什么来增加我们完成Megacorp交易的机会，并用它来帮助将来的交易。 人们总是在做假设分析时一直这样做：人们可以想象CEO在思考“如果只有我亲自回答了Megacorp关于我们服务的问题”或“我想知道如果我们给他们折扣，会发生什么，因为他们成为令人印象深刻的客户。” 我们需要了解的是，这些行为都不能保证销售，但是它们可以增加销售的几率，而运用多元宇宙理论，我们可以想象将没有进行销售的宇宙翻转为进行销售的宇宙。 在下图中，我演示了Normalcorp客户的情况，该客户最初有50％的销售机会，因为从50％的增长很容易看到。

I hope that viewing event probabilities using multiverse theory helps close the gap between understanding simple probabilities often used in stats courses (e.g. flipping coins, rolling dice, or pulling cards out a deck) and complex ones in the real world (e.g. probability of closing a sale, likelihood of converting a user to a paid subscription plan). For some fun explorations of thinking about probabilities through multiverses, I’d recommend the Remedial Chaos Theory episode (and subsequent ones that reference it) of Community, in which a die roll creates multiple timelines, and all of Rick and Morty. Try it out for yourself, share and discuss the idea with others — including me, I’ll do my best to respond to comments here or on Twitter, and see if it helps makes sense of complex real world phenomena and enables more rational decision-making.

我希望使用多元宇宙论来查看事件概率有助于缩小理解统计课程中经常使用的简单概率(例如，掷硬币，掷骰子或从牌组中抽出卡)与现实世界中复杂的概率(例如，关闭概率)之间的差距。销售，将用户转换为付费订阅计划的可能性)。 对于通过多元宇宙思考概率的一些有趣的探索，我建议使用“社区的补救混沌理论”一集(以及随后的参考书集) ，其中掷骰创建多个时间轴，以及所有Rick和Morty 。 亲自尝试一下，与他人分享并讨论这个想法-包括我在内，我将尽力在此处或在Twitter上回应评论，看看它是否有助于理解现实世界中的复杂现象并做出更合理的决策-制造。