FPCA is traditionally implemented with R but the “FDASRSF” package from J. Derek Tucker will achieve similar (and even greater) results in Python.

FPCA传统上是使用R实现的，但是J. Derek Tucker的“ FDASRSF ”软件包将在Python中获得相似(甚至更高)的结果。

If you have reached this page, you are probably familiar with PCA.

如果您已到达此页面，则可能熟悉PCA。

Principal Components Analysis is part of the Data Science exploration toolkit as it provides many benefits: reducing dimensions of a large dataset, preventing multi-collinearity, etc.

主成分分析是数据科学探索工具包的一部分，因为它具有许多优点：减少大型数据集的维数，防止多重共线性等。

There are many articles out there that explain the benefits of PCA and, if needed, I suggest you to have a look at this one which summarizes my understanding of this methodology:

那里有很多文章解释了PCA的好处，如果需要的话，我建议您看一下这篇文章，总结一下我对这种方法的理解：

“功能性” PCA背后的直觉 (The intuition behind the “Functional” PCA)

In a standard PCA process, we define Eigenvectors to convert the original dataset into a smaller one with fewer dimensions and for which most of the initial dataset variance is preserved (usually 90 or 95%).

在标准PCA流程中，我们定义特征向量以将原始数据集转换为尺寸较小的较小数据集，并为此保留了大部分初始数据集差异(通常为90％或95％)。

Now let’s imagine that the patterns of the time-series have more importance than their absolute variance. For example, you would like to compare physical phenomena such as signals, temperatures’ variation, production batches, etc.. Functional Principal Components Analysis will act this way by determining the corresponding underlying functions!

现在，让我们想象一下时间序列的模式比其绝对方差更重要。 例如，您想比较诸如信号，温度变化，生产批次等物理现象。功能主成分分析将通过确定相应的基础功能来执行此操作！

Let’s take the example of the temperatures’ variation over a year across different locations in a four-seasons country: we can assume that there is a global trend from cold in winter to hot during summertime.

让我们以一个四个季节的国家中不同位置一年中温度的变化为例：我们可以假设存在从冬季寒冷到夏季炎热的全球趋势。

We can also assume that the regions close to the ocean will follow a different pattern than the ones close to mountains (i.e.: smoother temperature variations on the sea-side Vs extremely low temperatures during winter in the mountains).

我们还可以假设，靠近海洋的地区将遵循与靠近山脉的地区不同的模式(即：海边的温度变化更为平稳，而山区冬季的极端低温则相对较低)。

We will now use this methodology to identify such differences between French regions in 2019. This example is directly inspired by the traditional “Canadian weather” FPCA example developed in R.

现在，我们将使用此方法来确定2019年法国各地区之间的差异。此示例直接受到R中开发的传统“加拿大天气” FPCA示例的启发。

2019年按地区划分的法国温度数据集 (Dataset creation with French temperatures by regions in 2019)

We start by getting daily temperature records since 2018 in France by regions* and prepare the corresponding dataset.

我们首先获取自2018年以来法国各地区的每日温度记录*，并准备相应的数据集。

(*the temperatures are recorded at the “department” level, which is a smaller scale than regions in France (96 departments Vs 13 regions). However, we rename “Department” into “Region” for an easier understanding of readers.)

(*温度记录在“部门”级别，该范围比法国的区域小(96个部门对13个区域)。但是，我们将“部门”重命名为“区域”，以便于读者理解。)

We select 7 regions spread across France that correspond to different weather patterns (they will be disclosed later on): 06, 25, 59, 62, 83, 85, 75.

我们选择了分布在法国的7个区域，分别对应不同的天气模式(稍后将进行披露)：06、25、59、62、83、85、75。

import pandas as pd
import numpy as np# Import the CSV file with only useful columns
# source: https://www.data.gouv.fr/fr/datasets/temperature-quotidienne-departementale-depuis-janvier-2018/
df = pd.read_csv("temperature-quotidienne-departementale.csv", sep=";", usecols=[0,1,4])# Rename columns to simplify syntax
df = df.rename(columns={"Code INSEE département": "Region", "TMax (°C)": "Temp"})# Select 2019 records only
df = df[(df["Date"]>="2019-01-01") & (df["Date"]<="2019-12-31")]# Pivot table to get "Date" as index and regions as columns 
df = df.pivot(index='Date', columns='Region', values='Temp')# Select a set of regions across France
df = df[["06","25","59","62","83","85","75"]]display(df)# Convert the Pandas dataframe to a Numpy array with time-series only
f = df.to_numpy().astype(float)# Create a float vector between 0 and 1 for time index
time = np.linspace(0,1,len(f))

FDASRSF软件包在数据集上的安装和使用 (FDASRSF package installation and use on the dataset)

To install the FDASRSF package in your current environment, you simply need to run:

要在当前环境中安装FDASRSF软件包，您只需要运行：

pip install fdasrsf

(note: based on my experience, you might need to install manually one or two additional packages to complete the installation properly. You just need to check the anaconda logs in case of failure to identify them.)

(注意：根据我的经验，您可能需要手动安装一个或两个其他软件包才能正确完成安装。您只需检查anaconda日志以防无法识别它们。)

The FDASRSF package from J. Derek Tucker provides a number of interesting functions and we will use two of them: Functional Alignment and Functional Principal Components Analysis (see corresponding documentation below):

J. Derek Tucker的FDASRSF软件包提供了许多有趣的功能，我们将使用其中两个功能 ： 功能对齐和功能主成分分析 (请参见下面的相应文档) ：

Functional Alignment will synchronize time-series in case they are not perfectly aligned. The illustration below provides a relatively simple example to understand this mechanism. The time-series are processed from both phase and amplitude’s perspectives (aka x and y axis).

如果它们未完全对齐， 功能对齐将同步时间序列。 下图提供了一个相对简单的示例来了解此机制。 从相位和幅度的角度(也称为x和y轴)角度处理时间序列。

To understand more precisely the algorithms involved, I highly recommend you to have a look at “Generative models for functional data using phase and amplitude separation” from J. Derek Tucker, Wei Wu, and Anuj Srivastava.

为了更精确地理解所涉及的算法，我强烈建议您看一下J. Derek Tucker，Wei Wu和Anuj Srivastava的“ 使用相位和幅度分离的功能数据生成模型 ”。

Even though this is quite hard to notice by simply looking at the Original and Warped Data, we can observe that the Warping functions do have some small inflections (see the yellow curve slightly lagging below the x=y axis), which means than these functions have synchronized the time series when needed. (As you might have guessed, temperature records are — by design — well aligned since they are captured simultaneously.)

尽管仅通过查看原始数据和变形数据很难注意到这一点，但我们可以观察到变形函数确实有一些小变形(请参见黄色曲线略微滞后于x = y轴)，这意味着这些函数比在需要时已同步时间序列。 (您可能已经猜到，温度记录在设计上是一致的，因为它们是同时捕获的。)

Functional Principal Components Analysis

功能主成分分析

Now that our dataset is “warped”, we can run a Functional Principal Components Analysis. The FDASRSF package allows horizontal, vertical, or joint analysis. We will use the vertical one and plot the corresponding functions and coefficients for PC1 & PC2.

现在我们的数据集已经“扭曲”了，我们可以运行功能主成分分析了。 FDASRSF软件包允许进行水平，垂直或联合分析。 我们将使用垂直的一个，并绘制PC1和PC2的相应函数和系数。

from fdasrsf import fPCA, time_warping, fdawarp, fdahpca# Functional Alignment
# Align time-series
warp_f = time_warping.fdawarp(f, time)
warp_f.srsf_align()warp_f.plot()# Functional Principal Components Analysis# Define the FPCA as a vertical analysis
fPCA_analysis = fPCA.fdavpca(warp_f)# Run the FPCA on a 3 components basis 
fPCA_analysis.calc_fpca(no=3)
fPCA_analysis.plot()import plotly.graph_objects as go# Plot of the 3 functions
fig = go.Figure()# Add traces
fig.add_trace(go.Scatter(y=fPCA_analysis.f_pca[:,0,0], mode='lines', name="PC1"))
fig.add_trace(go.Scatter(y=fPCA_analysis.f_pca[:,0,1], mode='lines', name="PC2"))
fig.add_trace(go.Scatter(y=fPCA_analysis.f_pca[:,0,2], mode='lines', name="PC3"))fig.update_layout(title_text='<b>Principal Components Analysis Functions</b>', title_x=0.5,
)fig.show()# Coefficients of PCs against regions
fPCA_coef = fPCA_analysis.coef# Plot of PCs against regions
fig = go.Figure(data=go.Scatter(x=fPCA_coef[:,0], y=fPCA_coef[:,1], mode='markers+text', text=df.columns))fig.update_traces(textposition='top center')fig.update_layout(autosize=False,width=800,height=700,title_text='<b>Function Principal Components Analysis on 2018 French Temperatures</b>', title_x=0.5,xaxis_title="PC1",yaxis_title="PC2",
)
fig.show()

Now we can add the different weather patterns on the plot, according to the weathers observed in France:

现在，根据法国观察到的天气，我们可以在地块上添加不同的天气模式：

很容易看出聚类与法国观测到的天气的吻合程度。 (It is easy to see how well the clustering fits with the observed weathers in France.)

It is also important to mention that I have chosen the departments arbitrarily according to the places where I live, work and travel frequently but they have not been selected because they were providing good results for this demo. I would expect the same quality of results with other regions.

还要提一提的是，我根据我经常居住，工作和旅行的地点随意选择了部门，但由于他们在此演示中提供了良好的结果，因此未选择这些部门。 我希望结果与其他地区的质量相同。

Maybe you are wondering if a standard PCA would also provide an interesting result?

也许您想知道标准PCA是否还会提供有趣的结果？

The plot here-below of standard PC1 and PC2 extracted from the original dataset shows that it is not performing as well as FPCA:

以下是从原始数据集中提取的标准PC1和PC2的图，显示其性能不如FPCA：

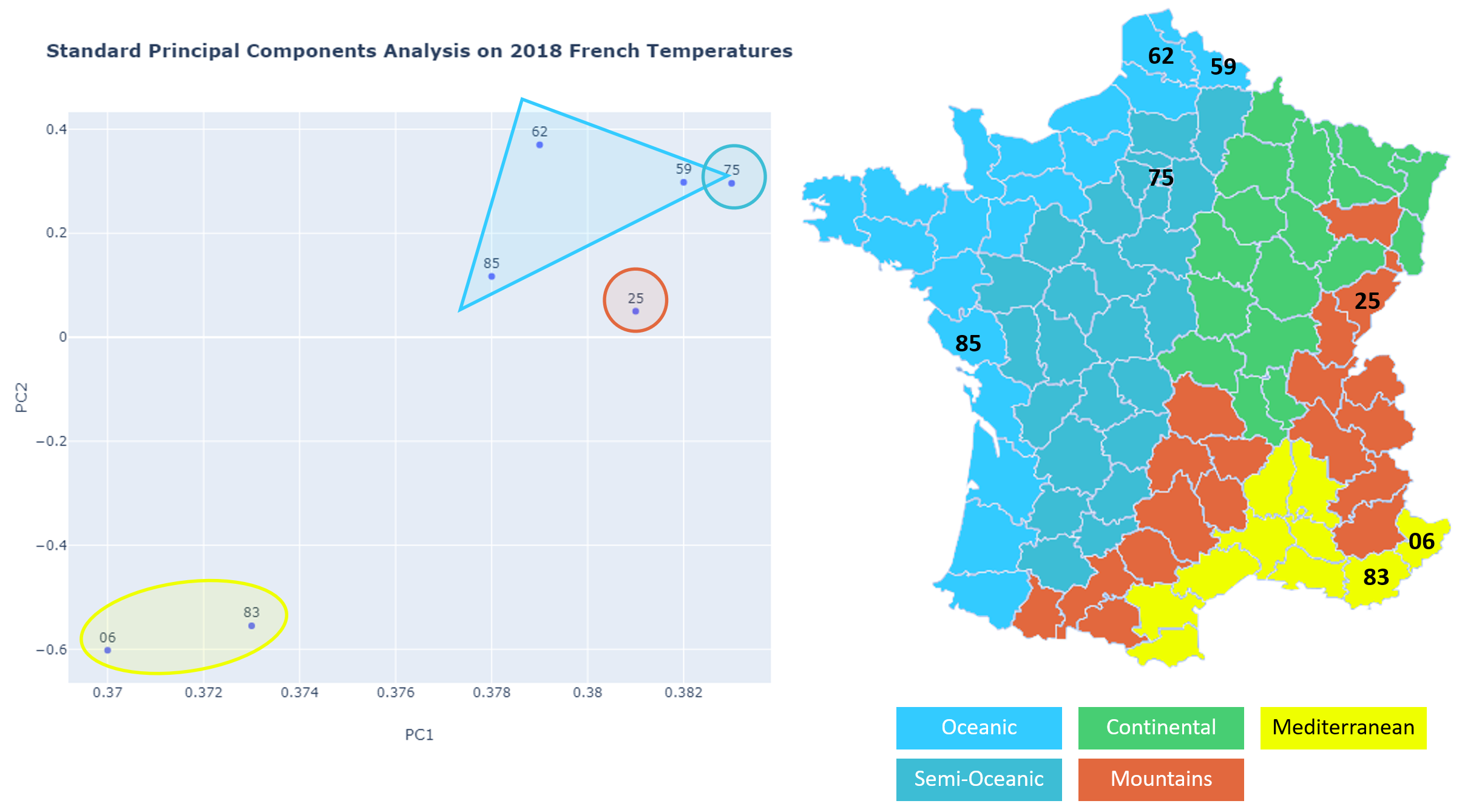
I hope this article has provided a better understanding of the Functional Principal Components Analysis to you.

希望本文为您提供了对功能主成分分析的更好理解。

I would also like to warmly thank J. Derek Tucker who has been kind enough to patiently guide me through the use of the FDASRSF package.

我还要衷心感谢J. Derek Tucker，他很友好地耐心指导我使用FDASRSF软件包。

The complete notebook is stored here.

完整的笔记本存储在此处 。

Here are some other articles you might like as well:

以下是您可能还会喜欢的其他一些文章：