为什么需要中间件
我们可能需要对每个请求/返回做一些特定的操作,比如
- 记录请求的 log 信息
- 在返回中插入一个 Header
- 部分接口进行鉴权
这些都需要一个统一的入口。这个功能可以通过引入 middleware 中间件来解决。Go 的 net/http 设计的一大特点是特别容易构建中间件。apiserver 所使用的 gin 框架也提供了类似的中间件。
gin里面的中间件
在 gin 中可以设置 3 种类型的 middleware:
- 全局中间件
router := gin.New()
// 添加自定义的 logger 中间件
router.Use(middleware.Logger(), gin.Recovery())
- 单个路由中间件
userRouter.GET("/profile/", middleware.Auth(), handler.UserProfile)
userRouter.POST("/update", middleware.Auth(), handler.UpdateUserProfile)
- 群组中间件
authorized := router.Group("/", MyMiddelware())
// 或者这样用:
authorized := router.Group("/")
authorized.Use(MyMiddelware())
{authorized.POST("/login", loginEndpoint)
}
在请求和返回的 Header 中插入 X-Request-Id
X-Request-Id 值为 32 位的 UUID,用于唯一标识一次 HTTP 请求
func RequestId() gin.HandlerFunc{return func(c *gin.Context) {requestId := c.Request.Header.Get("X-Request-Id")if requestId==""{v4:= uuid.NewV4()requestId=v4.String()}c.Set("X-Request-Id", requestId)c.Writer.Header().Set("X-Request-Id", requestId)c.Next()}日志中间件
- 获取请求路径,并且进行匹配(只对业务逻辑进行日志记录)
path := c.Request.URL.Pathreg:= regexp.MustCompile("(/v1/user|/login)")if !reg.MatchString(path) {return}// Skip for the health check requests.if path == "/sd/health" || path == "/sd/ram" || path == "/sd/cpu" || path == "/sd/disk" {return}
- 获取请求中的IP等信息,并且给请求重新赋值(请求读取完会被置空)
var bodys []byteif c.Request.Body!=nil{bodys, _ = ioutil.ReadAll(c.Request.Body)}c.Request.Body = ioutil.NopCloser(bytes.NewBuffer(bodys))method := c.Request.Methodip := c.ClientIP()- 将响应重定向到指定IO流,并且提取里面的信息
blw := &bodyLogWriter{body: bytes.NewBufferString(""),ResponseWriter: c.Writer,}c.Writer=blwc.Next()var response handler.Responseif err := json.Unmarshal(blw.body.Bytes(), &response); err != nil {log.Println(err, "response body can not unmarshal to model.Response struct, body: %s", string(blw.body.Bytes()))code = errno.InternalServerError.Codemessage = err.Error()} else {code = response.Codemessage = response.Message}}
func (w bodyLogWriter) Write(b []byte) (int, error) {w.body.Write(b)return w.ResponseWriter.Write(b)
- 将从请求与响应中提取的信息进行输出
log.Printf("%-13s | %-12s | %s %s | {code: %d, message: %s}", sub, ip, pad.Right(method, 5, ""), path, code, message)
测试
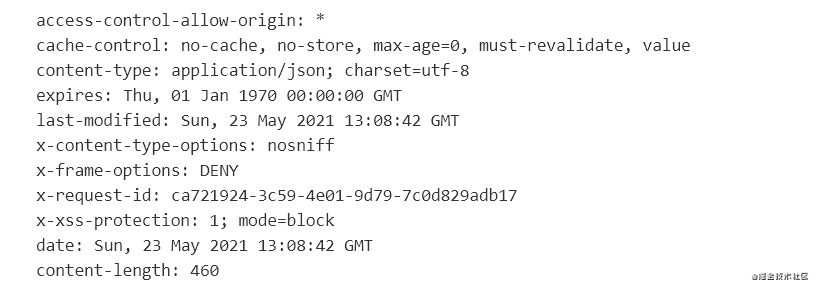
X-Request-id
可以看到,HTTP 返回的 Header 有 32 位的 UUID:
日志
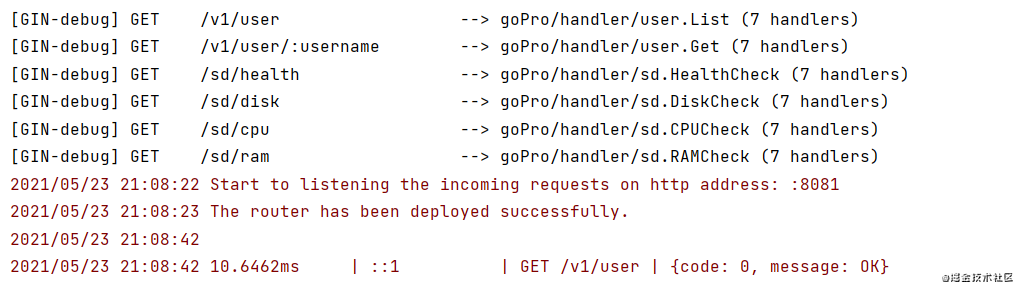
每个请求的日志信息分为4个部分
- 耗时
- 请求 IP
- HTTP 方法 HTTP 路径
- 返回的 Code 和 Message



)













)

