线性回归–最小二乘法(Least Square Method)
线性回归:
什么是线性回归?
举个例子,某商品的利润在售价为2元、5元、10元时分别为4元、10元、20元, 我们很容易得出商品的利润与售价的关系符合直线:y=2x. 在上面这个简单的一元线性回归方程中,我们称“2”为回归系数,即斜率为其回归系数。 回归系数表示商品的售价(x)每变动一个单位,其利润(y)与之对应的变动关系。
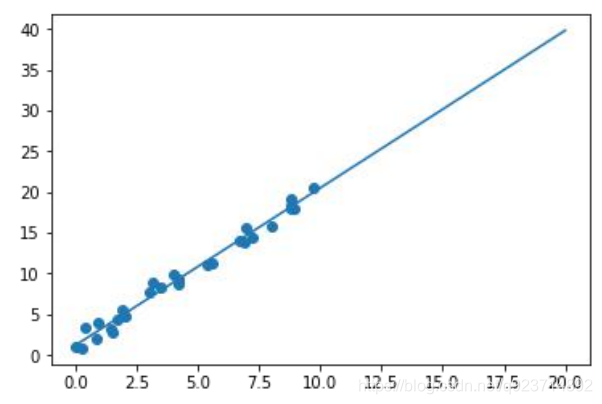
线性回归表示这些离散的点总体上“最逼近”哪条直线。
实现方法:
• 它通过最小化误差的平方和,寻找数据的最佳函数匹配。
• 利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方 和为最小。
• 假设我们现在有一系列的数据点(xi,yi) (i=1,…,m),那么由我们给出的拟合函数h(x)得到的估计量就 是h(xi)
• 残差:ri = h(xi) – yi
最小二乘法(Least Square Method)的概念
• 残差:ri = h(xi) – yi
• 三种范数:
1.∞-范数:残差绝对值的最大值,即所有数据点中残差距离的最大值:

2. 1-范数:绝对残差和,即所有数据点残差距离之和:
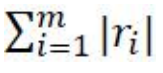
3. 2-范数:残差平方和:
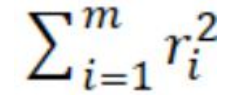
• 拟合程度,用通俗的话来讲,就是我们的拟合函数h(x)与待求解的函数y之间的相似性。那么 2-范数越小,自然相似性就比较高了。
最小二乘法的定义:
由此,我们可以写出最小二乘法的定义了:
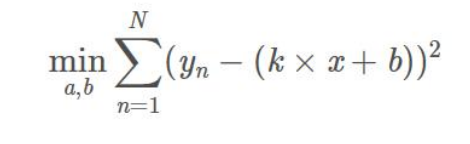
这是一个无约束的最优化问题,分别对k和b求偏导,然后令偏导数为0,即可获得极值点。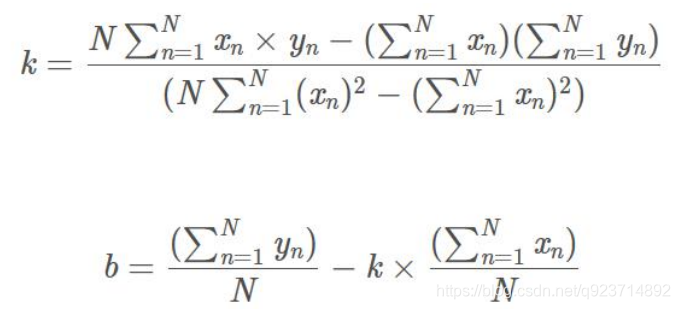
最小二乘法的代码实现:
import pandas as pdsales=pd.read_csv('train_data.csv',sep='\s*,\s*',engine='python') #读取CSV
X=sales['X'].values #存csv的第一列
Y=sales['Y'].values #存csv的第二列#初始化赋值
s1 = 0
s2 = 0
s3 = 0
s4 = 0
n = 4 ####你需要根据的数据量进行修改#循环累加
for i in range(n):s1 = s1 + X[i]*Y[i] #X*Y,求和s2 = s2 + X[i] #X的和s3 = s3 + Y[i] #Y的和s4 = s4 + X[i]*X[i] #X**2,求和#计算斜率和截距
k = (s2*s3-n*s1)/(s2*s2-s4*n)
b = (s3 - k*s2)/n
print("Coeff: {} Intercept: {}".format(k, b))
实验结果:
输入:
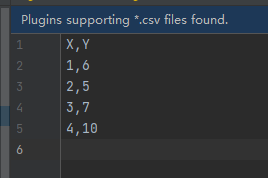
输出:

RANSAC(随机采样一致性)
RANSAC与最小二乘法
• 生产实践中的数据往往会有一定的偏差。
• 例如我们知道两个变量X与Y之间呈线性关系,Y=aX+b,我们想确定参数a与b的具体值。通过实验, 可以得到一组X与Y的测试值。虽然理论上两个未知数的方程只需要两组值即可确认,但由于系统误 差的原因,任意取两点算出的a与b的值都不尽相同。我们希望的是,最后计算得出的理论模型与测 试值的误差最小。
• 最小二乘法:通过计算最小均方差关于参数a、b的偏导数为零时的值。事实上,很多情况下,最小 二乘法都是线性回归的代名词。
• 遗憾的是,最小二乘法只适合于误差较小的情况。
• 在模型确定以及最大迭代次数允许的情况下,RANSAC总是能找到最优解。(对于包含80%误差的数 据集,RANSAC的效果远优于直接的最小二乘法。)
• 由于一张图片中像素点数量大,采用最小二乘法运算量大,计算速度慢。
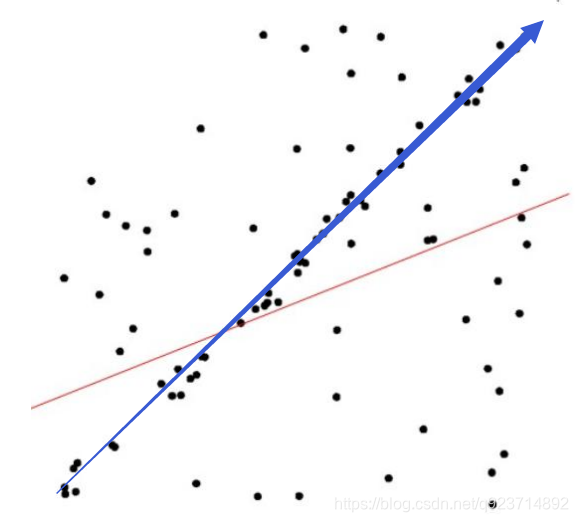
比如说:上图,通过肉眼很明显可以看出来拟合的线应该是蓝色的,然而经过最小二乘法后得到的是红色的线。
RANSAC的步骤:
RANSAC算法的输入:
- 一组观测数据(往往含有较大的噪声或无效点),
- 一个用于解释观测数据的参数化模型
- 一些可信的参数。
RANSAC算法的实现: - 在数据中随机选择几个点设定为内群
- 计算适合内群的模型
- 把其它刚才没选到的点带入刚才建立的模型中,计算是否为内群
- 记下内群数量
- 重复以上步骤
- 比较哪次计算中内群数量最多,内群最多的那次所建的模型就是我们所要求的解
注意:不同问题对应的数学模型不同,因此在计算模型参数时方法必定不同,RANSAC的作用不在于计 算模型参数,而是提供更好的输入数据(样本)。(这导致ransac的缺点在于要求数学模型已知)
RANSAC的参数确定:
这里有几个问题:
- 一开始的时候我们要随机选择多少点(n)
- 以及要重复做多少次(k)
• 假设每个点是真正内群的概率为 w: w = 内群的数目/(内群数目+外群数目)
• 通常我们不知道 w 是多少, w^n是所选择的n个点都是内群的机率, 1-w^n 是所选择的n个点至少有一个 不是内群的机率, (1 − wn)k 是表示重复 k 次都没有全部的n个点都是内群的机率, 假设算法跑 k 次以后 成功的机率是p,那么, 1 − p = (1 − wn)k p = 1 − (1 − wn)k
• 我们可以通过P反算得到抽取次数K,K=log(1-P)/log(1-w^n)。
• 所以如果希望成功机率高:
• 当n不变时,k越大,则p越大; 当w不变时,n越大,所需的k就越大。
• 通常w未知,所以n 选小一点比较好。
RANSAC的代码实现:
import numpy as np
import scipy as sp
import scipy.linalg as sldef ransac(data, model, n, k, t, d, debug = False, return_all = False):"""输入:data - 样本点model - 假设模型:事先自己确定n - 生成模型所需的最少样本点k - 最大迭代次数t - 阈值:作为判断点满足模型的条件d - 拟合较好时,需要的样本点最少的个数,当做阈值看待输出:bestfit - 最优拟合解(返回nil,如果未找到)iterations = 0bestfit = nil #后面更新besterr = something really large #后期更新besterr = thiserrwhile iterations < k {maybeinliers = 从样本中随机选取n个,不一定全是局内点,甚至全部为局外点maybemodel = n个maybeinliers 拟合出来的可能符合要求的模型alsoinliers = emptyset #满足误差要求的样本点,开始置空for (每一个不是maybeinliers的样本点){if 满足maybemodel即error < t将点加入alsoinliers }if (alsoinliers样本点数目 > d) {%有了较好的模型,测试模型符合度bettermodel = 利用所有的maybeinliers 和 alsoinliers 重新生成更好的模型thiserr = 所有的maybeinliers 和 alsoinliers 样本点的误差度量if thiserr < besterr{bestfit = bettermodelbesterr = thiserr}}iterations++}return bestfit"""iterations = 0bestfit = Nonebesterr = np.inf #设置默认值best_inlier_idxs = Nonewhile iterations < k:maybe_idxs, test_idxs = random_partition(n, data.shape[0])print ('test_idxs = ', test_idxs)maybe_inliers = data[maybe_idxs, :] #获取size(maybe_idxs)行数据(Xi,Yi)test_points = data[test_idxs] #若干行(Xi,Yi)数据点maybemodel = model.fit(maybe_inliers) #拟合模型test_err = model.get_error(test_points, maybemodel) #计算误差:平方和最小print('test_err = ', test_err <t)also_idxs = test_idxs[test_err < t]print ('also_idxs = ', also_idxs)also_inliers = data[also_idxs,:]if debug:print ('test_err.min()',test_err.min())print ('test_err.max()',test_err.max())print ('numpy.mean(test_err)',numpy.mean(test_err))print ('iteration %d:len(alsoinliers) = %d' %(iterations, len(also_inliers)) )# if len(also_inliers > d):print('d = ', d)if (len(also_inliers) > d):betterdata = np.concatenate( (maybe_inliers, also_inliers) ) #样本连接bettermodel = model.fit(betterdata)better_errs = model.get_error(betterdata, bettermodel)thiserr = np.mean(better_errs) #平均误差作为新的误差if thiserr < besterr:bestfit = bettermodelbesterr = thiserrbest_inlier_idxs = np.concatenate( (maybe_idxs, also_idxs) ) #更新局内点,将新点加入iterations += 1if bestfit is None:raise ValueError("did't meet fit acceptance criteria")if return_all:return bestfit,{'inliers':best_inlier_idxs}else:return bestfitdef random_partition(n, n_data):"""return n random rows of data and the other len(data) - n rows"""all_idxs = np.arange(n_data) #获取n_data下标索引np.random.shuffle(all_idxs) #打乱下标索引idxs1 = all_idxs[:n]idxs2 = all_idxs[n:]return idxs1, idxs2class LinearLeastSquareModel:#最小二乘求线性解,用于RANSAC的输入模型 def __init__(self, input_columns, output_columns, debug = False):self.input_columns = input_columnsself.output_columns = output_columnsself.debug = debugdef fit(self, data):#np.vstack按垂直方向(行顺序)堆叠数组构成一个新的数组A = np.vstack( [data[:,i] for i in self.input_columns] ).T #第一列Xi-->行XiB = np.vstack( [data[:,i] for i in self.output_columns] ).T #第二列Yi-->行Yix, resids, rank, s = sl.lstsq(A, B) #residues:残差和return x #返回最小平方和向量 def get_error(self, data, model):A = np.vstack( [data[:,i] for i in self.input_columns] ).T #第一列Xi-->行XiB = np.vstack( [data[:,i] for i in self.output_columns] ).T #第二列Yi-->行YiB_fit = sp.dot(A, model) #计算的y值,B_fit = model.k*A + model.berr_per_point = np.sum( (B - B_fit) ** 2, axis = 1 ) #sum squared error per rowreturn err_per_pointdef test():#生成理想数据n_samples = 500 #样本个数n_inputs = 1 #输入变量个数n_outputs = 1 #输出变量个数A_exact = 20 * np.random.random((n_samples, n_inputs))#随机生成0-20之间的500个数据:行向量perfect_fit = 60 * np.random.normal( size = (n_inputs, n_outputs) ) #随机线性度,即随机生成一个斜率B_exact = sp.dot(A_exact, perfect_fit) # y = x * k#加入高斯噪声,最小二乘能很好的处理A_noisy = A_exact + np.random.normal( size = A_exact.shape ) #500 * 1行向量,代表XiB_noisy = B_exact + np.random.normal( size = B_exact.shape ) #500 * 1行向量,代表Yiif 1:#添加"局外点"n_outliers = 100all_idxs = np.arange( A_noisy.shape[0] ) #获取索引0-499np.random.shuffle(all_idxs) #将all_idxs打乱outlier_idxs = all_idxs[:n_outliers] #100个0-500的随机局外点A_noisy[outlier_idxs] = 20 * np.random.random( (n_outliers, n_inputs) ) #加入噪声和局外点的XiB_noisy[outlier_idxs] = 50 * np.random.normal( size = (n_outliers, n_outputs)) #加入噪声和局外点的Yi#setup model all_data = np.hstack( (A_noisy, B_noisy) ) #形式([Xi,Yi]....) shape:(500,2)500行2列input_columns = range(n_inputs) #数组的第一列x:0output_columns = [n_inputs + i for i in range(n_outputs)] #数组最后一列y:1debug = Falsemodel = LinearLeastSquareModel(input_columns, output_columns, debug = debug) #类的实例化:用最小二乘生成已知模型linear_fit,resids,rank,s = sp.linalg.lstsq(all_data[:,input_columns], all_data[:,output_columns])#run RANSAC 算法ransac_fit, ransac_data = ransac(all_data, model, 50, 1000, 7e3, 300, debug = debug, return_all = True)if 1:import pylabsort_idxs = np.argsort(A_exact[:,0])A_col0_sorted = A_exact[sort_idxs] #秩为2的数组if 1:pylab.plot( A_noisy[:,0], B_noisy[:,0], 'k.', label = 'data' ) #散点图pylab.plot( A_noisy[ransac_data['inliers'], 0], B_noisy[ransac_data['inliers'], 0], 'bx', label = "RANSAC data" )else:pylab.plot( A_noisy[non_outlier_idxs,0], B_noisy[non_outlier_idxs,0], 'k.', label='noisy data' )pylab.plot( A_noisy[outlier_idxs,0], B_noisy[outlier_idxs,0], 'r.', label='outlier data' )pylab.plot( A_col0_sorted[:,0],np.dot(A_col0_sorted,ransac_fit)[:,0],label='RANSAC fit' )pylab.plot( A_col0_sorted[:,0],np.dot(A_col0_sorted,perfect_fit)[:,0],label='exact system' )pylab.plot( A_col0_sorted[:,0],np.dot(A_col0_sorted,linear_fit)[:,0],label='linear fit' )pylab.legend()pylab.show()if __name__ == "__main__":test()实现结果:
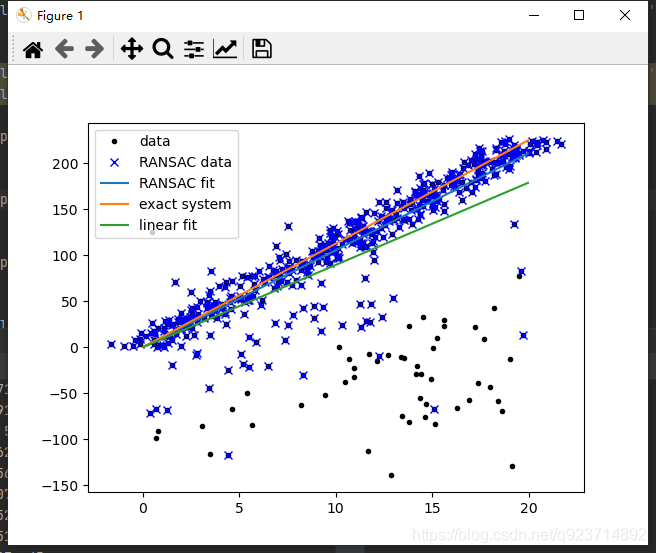
注意:特别注意:这个算法应该数据是随机初始的,可能出现did't meet fit acceptance criteria的错误,多运行几次有几率解决。
结果很明显可以看出:ransac模型比linear模型更加接近exact system。
RANSAC的应用:
全景拼接:
流程:
- 针对某个场景拍摄多张/序列图像
- 通过匹配特征(sift匹配)计算下一张图像与上一张图像之间的变换结构。
- 图像映射,将下一张图像叠加到上一张图像的坐标系中
- 变换后的融合/合成



RANSAC的优缺点:
优点:
- 它能鲁棒的估计模型参数。例如,它能从包含大量局外点的数据集中估计出高精度的参数。
缺点:
- 它计算参数的迭代次数没有上限;如果设置迭代次数的上限,得到的结果可能不是最优的结果,甚至可能得到错误的结果。
- RANSAC只有一定的概率得到可信的模型,概率与迭代次数成正比。
- 它要求设置跟问题相关的阀值。
- RANSAC只能从特定的数据集中估计出一个模型,如果存在两个(或多个)模型,RANSAC不能找到 别的模型。
- 要求数学模型已知(这个缺点最致命)




)

和归一化实现)


 or ‘1type‘ as a synonym of type is deprecated解决办法)
转移方式及参数传递)








