To study structure,tear away all flesh soonly the bone shows.

要研究结构，请尽快撕掉骨头上所有的肉。

Linear algebra. Graph theory. If you are a data scientist, you have encountered both of these fields in your study or work at some point. They are part of a standard curriculum, frequently used tools in the kit of every engineer.

线性代数。 图论。 如果您是数据科学家，则在研究或工作中有时会遇到这两个领域。 它们是标准课程的一部分，是每个工程师工具包中常用的工具。

What is rarely taught, however, is that they have a very close and fruitful relationship. Graphs can be used to prove strong structural results about matrices easily and beautifully.

但是，很少有人教给他们，他们之间的关系非常密切而富有成果。 图可以用来轻松，美观地证明矩阵的强大结构结果。

To begin our journey, first, we shall take a look at how a matrix can be described with a graph.

首先，我们将看看如何用图形描述矩阵。

矩阵作为图 (Matrices as graphs)

Suppose that we have a square matrix

假设我们有一个方矩阵

We say that the weighted and directed graph

我们说加权有向图

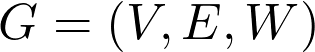
corresponds to A if

对应于A，如果

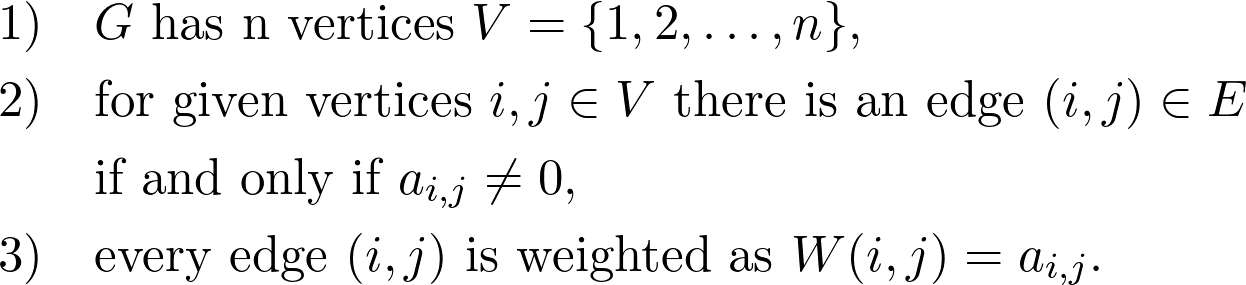
If this sounds complicated, here is an example.

如果这听起来很复杂，请举一个例子。

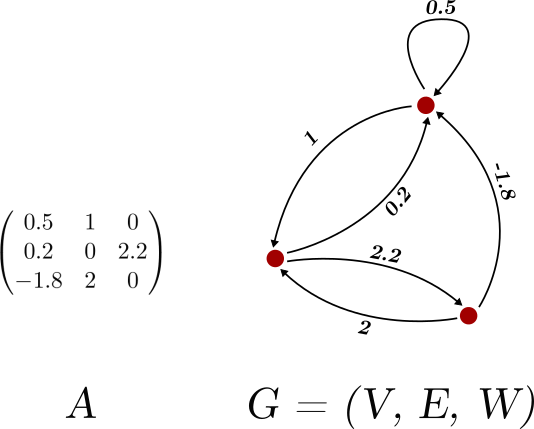
So, for every square matrix, we have a weighted and directed graph. In general, having distinct representations for the same object is colossally useful in mathematics. Sometimes, complex things can be significantly simplified the moment you start looking at things from a different perspective.

因此，对于每个方阵，我们都有一个加权有向图。 通常，对于同一对象具有不同的表示形式在数学中非常有用。 有时，从开始以不同的角度看待事物时，复杂的事物就可以大大简化。

Such as the case of matrices and graphs.

例如矩阵和图形的情况。

在图上走动 (Walking around the graph)

A great feature of the graph representation is the ability to visualize matrix powers.

图形表示的一个很大的特点是可视化矩阵幂的能力。

Suppose that the k-th power of A is denoted by

假设A的k次幂表示为

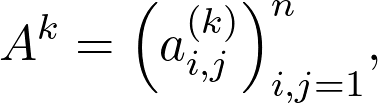
where k can be any positive integer. For k = 2, it is calculated by

其中k可以是任何正整数。 对于k = 2 ，其计算公式为

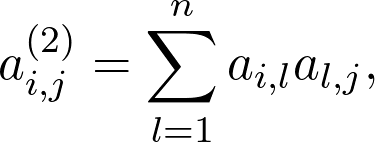
which seems pretty mystical.

这似乎很神秘。

With graphs, there is a pretty simple explanation.

对于图形，有一个非常简单的解释。

For any two nodes i and j, there are several ways to go from one to another. These are called walks. In general, a walk is defined by the sequence of vertices

对于任何两个节点i和j ，有几种方法可以从一个转移到另一个。 这些被称为步行 。 通常，走行由顶点序列定义

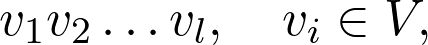
where there must be an edge between vᵢ and vᵢ₊₁. Since the graph of the matrix is weighted, we can define the weight of the walk as well by multiplying the weights of each edge traversed:

在vᵢ和vᵢ₊₁之间必须有一条边。 由于矩阵的图形是加权的，因此我们也可以通过将遍历的每个边的权重相乘来定义步行的权重：

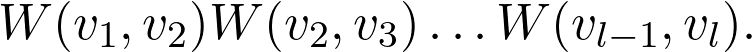
(To motivate the definition, let’s suppose we are talking about a transition graph of a discrete Markov chain. In this case, the weight of a walk would equal to the probability of having consecutive states corresponding to the prescribed walk.)

(为激发定义，让我们假设我们正在谈论离散马尔可夫链的转移图。在这种情况下，步行的权重将等于具有对应于规定步行的连续状态的概率。)

So, in graph terminology,

因此，在图形术语中，

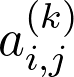
equals to the sum of weights for all possible k-long paths between i and j. This is easy to see for k = 2, and the general case follows from this using induction.

等于i和j之间所有可能的k长路径的权重之和。 对于k = 2来说 ，这很容易看到，并且一般情况是通过归纳法得出的。

混合起来(字面意思) (Mixing things up (literally))

If you are familiar with some advanced topics in linear algebra, you must have encountered the concept of similar matrices. A and B are called similar if there is a matrix P such that

如果您熟悉线性代数的一些高级主题，那么您一定已经遇到过类似矩阵的概念。 如果存在一个矩阵P使得A和B 相似

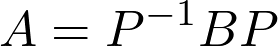
holds. This is a very important concept. If we think of matrices as linear transformations, similarity means that A and B are essentially the same transformations, only in a different coordinate system. (And P is the change of coordinates.)

持有。 这是一个非常重要的概念。 如果我们将矩阵视为线性变换，则相似性意味着A和B本质上是相同的变换，只是在不同的坐标系中。 ( P是坐标的变化。)

For example, some matrices can be diagonalized with similarity transformations. So, if we look at them using a special coordinate system, a complicated matrix may just describe a simple stretching.

例如，某些矩阵可以通过相似性变换进行对角化。 因此，如果我们使用特殊的坐标系查看它们，则复杂的矩阵可能只是描述了简单的拉伸。

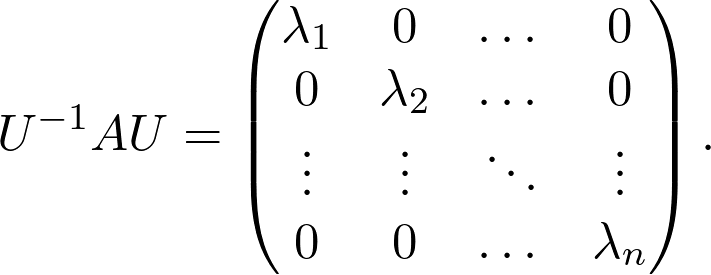
An important special case is where the similarity matrix P is a so-called permutation matrix.

一个重要的特殊情况是，相似矩阵P是所谓的置换矩阵 。

置换矩阵 (Permutation matrices)

In mathematics, any bijective mapping

在数学中，任何双射映射

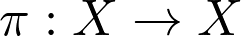
is called a permutation. Specifically, if X = {1, 2, …, n}, then π is simply a reordering of the numbers.

称为排列。 具体来说，如果X = {1,2，…，n} ，则π只是数字的重新排序。

Any such permutation can be represented with a matrix, defined by

任何这样的排列都可以用一个矩阵表示，该矩阵由

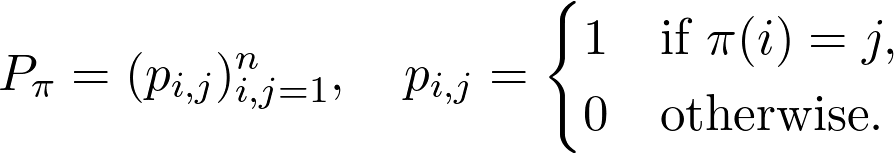
If this is not easy to understand, no worries, I’ll give an example right now. For the permutation defined by

如果这不容易理解，不用担心，我现在就举一个例子。 对于由定义的排列

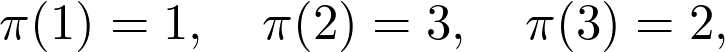
we have

我们有

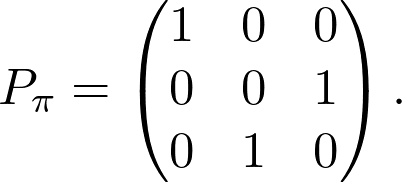
Why do we define the permutation matrix this way? To see this, consider the following:

为什么我们用这种方式定义置换矩阵？ 要看到这一点，请考虑以下因素：

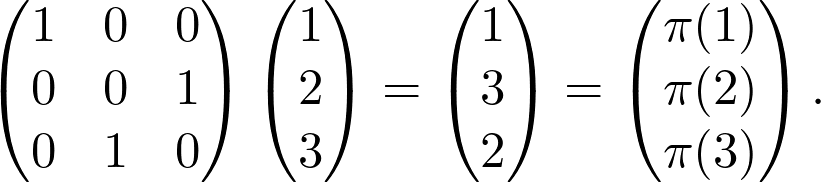
Multiplying a matrix with a permutation matrix shuffles its rows or columns, depending on whether we multiply from the left or right, so we have

将矩阵与置换矩阵相乘会改变其行或列，具体取决于我们是从左侧还是右侧进行乘法运算，因此

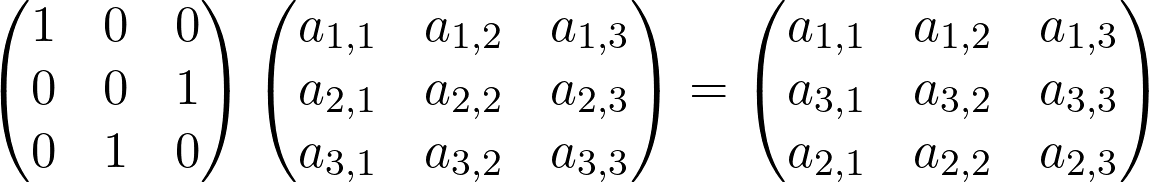
and

和

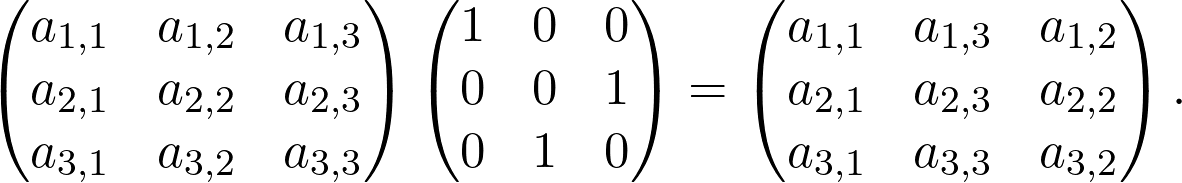
(Recall that matrix multiplication is not commutative.)

(回想一下，矩阵乘法不是可交换的。)

The inverse of a permutation matrix is its transpose. This is easy to see, once you explicitly calculate the product

置换矩阵的逆是它的转置。 一旦您明确计算出乘积，这很容易看到

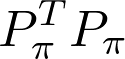
by hand.

用手。

置换矩阵的相似性变换 (Similarity transforms with permutation matrices)

So, let’s go back to graphs and matrices. For a given permutation matrix and a matrix A, what does the similarity transform do? If you think about it, the matrix

因此，让我们回到图和矩阵。 对于给定的置换矩阵和矩阵A ，相似度变换做什么？ 如果您考虑一下，矩阵

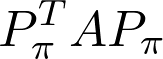
contains identical elements, just its rows and columns are shuffled. In fact, their corresponding graphs are isomorphic with each other. (Which is a fancy expression for being the same after relabeling certain vertices.) Although showing this might look difficult, it can be done by simply noting three key things.

包含相同的元素，只是其行和列被改组。 实际上，它们对应的图彼此同构。 (在重新标注某些顶点后，这是一个很好的表达方式，因为它是相同的。)尽管显示这一点看起来很困难，但可以通过简单地注意三个关键事项来完成。

• The graph of APπ can be obtained from the graph of A by taking all edges (i, j) and replacing them with (i, π(j)).

  通过取所有边(i，j)并将其替换为(i，π(j))可以从A的图获得APπ的图。

• Similarly, the graph of PπᵀA can be obtained by replacing (i, j) with

  类似地，可以通过将(i，j)替换为PπᵀA的图

  Similarly, the graph of PπᵀA can be obtained by replacing (i, j) with (π⁻¹(i), j ).

  类似地，可以通过用(π11(i)，j)代替(i，j)来获得PπᵀA的图。

• Every permutation graph can be written as a product of permutation matrices where only two elements are swapped. These are called transpositions and their inverses are themselves.

  每个排列图都可以写成仅交换两个元素的排列矩阵的乘积。 这些被称为换位 ，它们的逆本身。

矩阵的结构 (The structure of matrices)

A central question in the theory of matrices is to simplify and reveal their underlying structure by some kind of transformation, like similarity.

矩阵理论中的一个中心问题是通过某种转换(例如相似性)来简化和揭示其基本结构。

For example, as mentioned, certain matrices can be diagonalized by a similarity transformation:

例如，如前所述，某些矩阵可以通过相似性变换进行对角化：

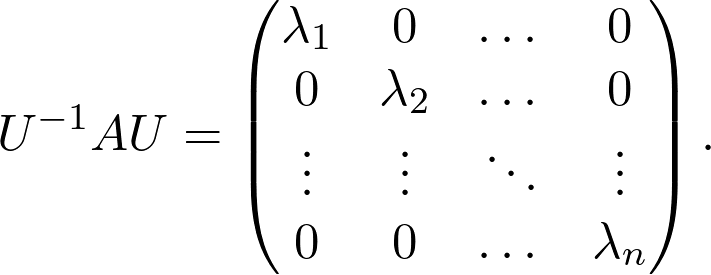
Note that this is not true for all matrices. (Check out the spectral theorem if you are interested.) Diagonal matrices are special and easy to work with, so when diagonalization is possible, our job is much simpler.

请注意，并非所有矩阵都是如此。 ( 如果您有兴趣，请查看频谱定理。 )对角矩阵是特殊的并且易于使用，因此，在可能进行对角化的情况下，我们的工作会简单得多。

Another special form is the block-triangular form. The matrix A is upper block-triangular, if there are submatrices B, C, D such that

另一个特殊形式是块三角形形式。 如果存在子矩阵B，C，D ，则矩阵A为上块三角形

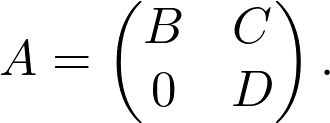
(Note that 0 is a matrix with all zeros here.)

(请注意， 0是此处为全零的矩阵。)

Definition. A nonnegative matrix A is called reducible, if it can be upper block-triangularized with a similarity transform using a permutation matrix P:

定义。 如果非负矩阵A可以使用置换矩阵P进行相似度变换并进行上块三角化，则称为可约矩阵A ：

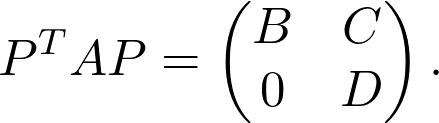
If it cannot be done, the matrix is called irreducible. From a graph-theoretical perspective, reducibility is equivalent to partitioning the nodes to two subsets S, T such that there are no outgoing edges from T to S.

如果无法完成，则将矩阵称为不可约 。 从图论的角度来看，可简化性等效于将节点划分为两个子集S，T ，这样就没有从T到S的传出边。

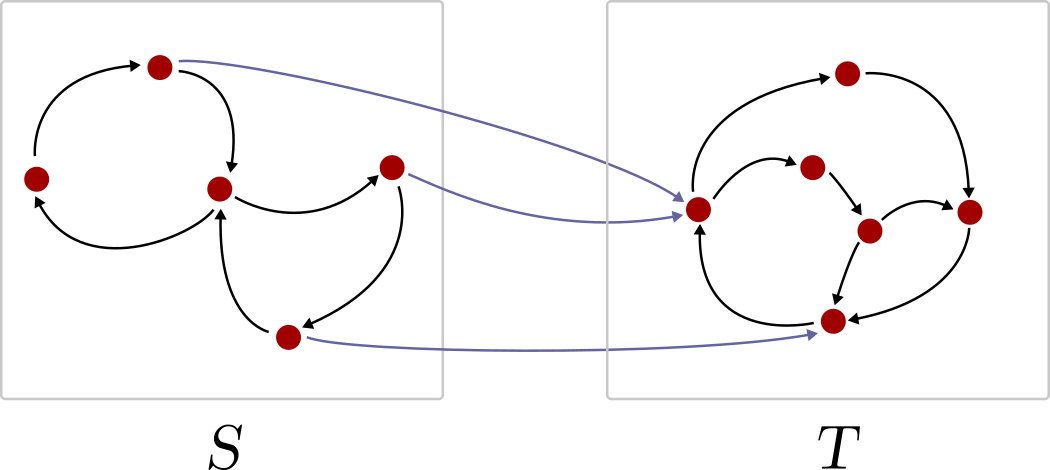
Imagine that you are randomly walking along the edges of this graph, like a Markov chain. Reducibility means that once you enter T, you cannot leave it. (And, if there is a nonzero probability to enter, you will enter eventually.)

想象一下，您像Markov链一样随机地沿着该图的边缘行走。 可简化性意味着，一旦输入T ，就无法离开它。 (并且，如果输入的可能性非零， 则最终将输入 。)

With irreducible and reducible matrices, nonnegative matrices can be significantly simplified, as we shall see next.

使用不可约矩阵和可约矩阵，可以显着简化非负矩阵，这将在后面看到。

Frobenius范式 (The Frobenius normal form)

Before going into explanations, let’s just state the theorem.

在进行解释之前，让我们先陈述定理。

Theorem. (Frobenius normal form) For every nonnegative matrix A, there is a permutation matrix P such that

定理。 (Frobenius范式)对于每个非负矩阵A ，都有一个置换矩阵P使得

where the Aᵢ -s are irreducible matrices.

其中Aᵢ- s是不可约矩阵。

This theorem is hard to prove using only the tools of algebra. (As it was done originally.) However, with graphs, it is almost trivial.

仅使用代数工具很难证明该定理。 (正如最初所做的那样。)但是，对于图形来说，这几乎是微不足道的。

To do this, let’s introduce the concept of strongly connectedness nodes in the graph. The nodes i and j are strongly connected if there is a directed walk from i to j AND a directed walk from j to i. That is, they are mutually reachable from each other.

为此，让我们在图中介绍强连接节点的概念。 如果存在从i到j的定向走和从j到i的定向走，则节点i和j是牢固连接的。 即，它们彼此可以相互到达。

In the language of algebra, the relation “i and j are strongly connected” is an equivalence relation. This means that they partition V into subsets V₁, V₂, …, Vₖ such that all vertices in Vᵢ are strongly connected, but NOT strongly connected with any other vertex.

用代数的语言来说，关系“ i和j紧密相连”是等价关系。 这意味着它们划分V输入子集V 1，V 2，...，Vₖ使得Vᵢ所有顶点是密切联系的，但与其他任何顶点非强连接。

For illustration, the graph looks something like this.

为了说明，该图看起来像这样。

Believe it or not, this proves the Frobenius theorem about the normal form. To see, we just have to renumber the vertices such that each strongly connected set of vertices are numbered consecutively. As we have seen, the renumbering of vertices is equivalent to applying a permutation transform. Hence,

信不信由你，这证明了Frobenius定理关于正规形式。 要看到，我们只需要对顶点重新编号，以使每个强连接的顶点集都被连续编号。 如我们所见，顶点的重编号等效于应用置换变换。 因此，

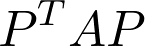
is of the desired form.

具有所需的形式。

This theorem illustrates the use of graph theory in linear algebra. By simply drawing a picture, so many structural patterns are revealed.

该定理说明了图论在线性代数中的使用。 通过简单地绘制图片，可以显示出许多结构模式。

Of course, this is just the tip of the iceberg. If you are interested, check out the book A Combinatorial Approach to Matrix Theory and Its Applications by Richard A. Brualdi and Dragos Cvetkovic, which is full of beautiful mathematics regarding this topic.

当然，这只是冰山一角。 如果您有兴趣，请阅读Richard A. Brualdi和Dragos Cvetkovic撰写的《矩阵理论及其应用的组合方法 》一书，其中充斥着与此主题相关的精美数学知识。

结论 (Conclusion)

Graphs and matrices go hand in hand. Specifically, graph theory provides a new way to think about matrices. Although this is usually not part of a standard curriculum in linear algebra, it is a fruitful connection between the two. With it, certain structural aspects of matrices become trivial.

图形和矩阵齐头并进。 具体来说，图论提供了一种思考矩阵的新方法。 尽管这通常不是线性代数标准课程的一部分，但这是两者之间卓有成效的联系。 有了它，矩阵的某些结构方面变得无关紧要。