The first quantitative class for vanilla finance and quantitative finance majors alike has to do with the time value of money. Essentially, it’s a semester-long course driving notions like $100 today is worth more than $100 a year from today into the heads of college students and making them work out painful word problems by hand to determine how much they need to invest today to arrive at some value in the future. This is done in tandem with the introduction to perpetuities and annuities as an application to the temporal value differential. Though I wasn’t a fan of working out the computations by hand, I’m a big fan of coding them in Python for ease of use.

吨他香草金融和计量金融专业第一定量类都与金钱的时间价值的事情。 本质上讲，这是一个学期的课程驱动概念，例如今天的100美元从今天起每年价值超过100美元，进入大学生的脑袋，并使他们手工解决痛苦的单词问题，以确定他们今天需要投入多少才能达到目标将来会有一些价值。 这是通过引入永久性和年金作为时间值微分的应用来完成的。 尽管我不喜欢手工进行计算，但我还是非常喜欢使用Python进行编码以便于使用。

金钱的时间价值 (Time Value of Money)

Risk-free interest rates — in practice proxied by U.S. treasury bills, notes, and bonds are responsible for the difference in the value of money over time. Higher-level courses covering subjects including derivatives and securities pricing always take into account the time value of money in their pricing formulae, making this topic what algebra is to calculus.

无风险利率-实际上是由美国国库券，票据和债券所代理，是货币价值随时间变化的原因。 涵盖衍生产品和证券定价等主题的高级课程始终在定价公式中考虑货币的时间价值，这使该主题成为微积分的代数。

Consider the current risk-free rate is 8% per annum. To receive $100 today means an immediate investment can be made at the risk-free rate…

考虑当前的无风险利率为每年8％。 今天要获得$ 100，意味着可以无风险的价格立即进行投资...

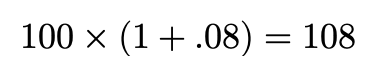
After a year $100 at the risk-free rate is $108. Therefore receiving $100 today would be worth more than receiving $100 one year from today all else equal.

一年后，以无风险利率计算的100美元为108美元。 因此接受$ 100今天的价值将超过从今天一切平等接受$ 100中的一个年份。

In the previous example, compounding (reinvesting periodic interest payments throughout the year) was completely disregarded. Let’s look at another example where we take into account a compounding effect.

在前面的示例中，完全忽略了复利(全年将定期利息支出再投资)。 让我们看另一个考虑复合效应的例子。

Consider the current risk-free rate is 8% per annum, and the compounding frequency is once per month. To receive $100 today means an immediate investment with monthly compounding can be made at the risk-free rate…

考虑当前的无风险利率为8％，复利频率为每月一次。 今天要获得$ 100的收益，就可以无风险的利率进行每月复利的即时投资…

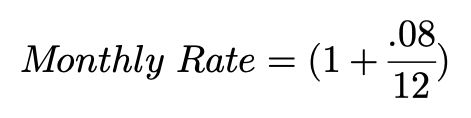
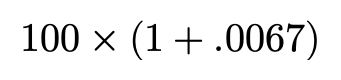
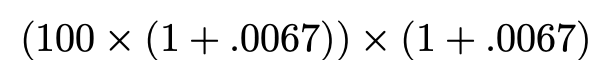
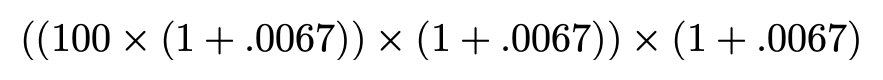
Hopefully, by now a pattern is recognized — for each month…

希望到目前为止，每个月都可以识别出一种模式。

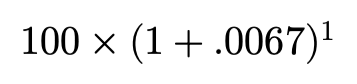
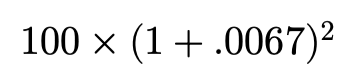
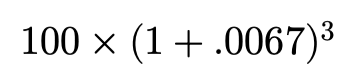
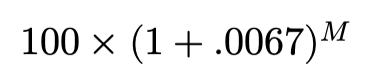
After a year $100 at the risk-free rate is approximately $108.34. It’s common to refer to the value in terms of “time-period dollars”. For example, $100 today is worth $108.34 in time-period 1 dollars…

一年后，按无风险利率计算，$ 100约为$ 108.34。 通常用“ 时间段美元 ”来表示值。 例如，今天$ 100在时间段内价值$ 108.34，即$ 1…

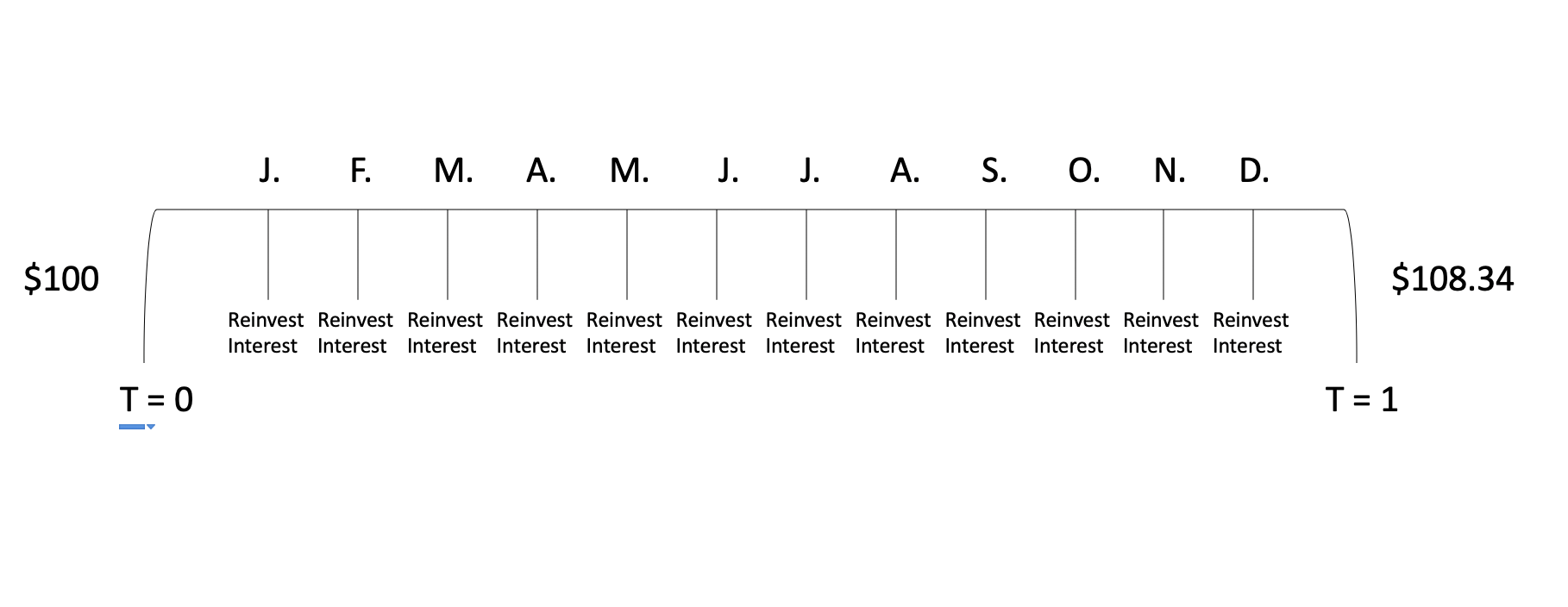
Therefore receiving $100 today would be worth more than receiving $100 today without monthly compounding all else equal.

因此，今天获得100美元的价值将比今天获得100美元的价值要多得多，而不必按月计算其他所有等式 。

From the examples above a general formula can be constructed…

根据以上示例，可以构造一个通用公式…

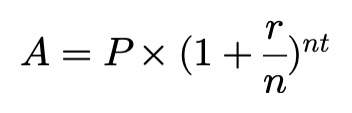
• P — initial amount or principal ($100)

  P-初始金额或本金($ 100)

• A — resulting amount in time-period t dollars ($108 or $108.34)

  A-时间周期内的最终金额(美元)($ 108或$ 108.34)

• r — risk-free rate of interest (8%)

  r —无风险利率(8％)

• n — compounding frequency for time-period t (1 or 12)

  n-时间段t的复合频率(1或12)

• t — time-periods to elapse (1)

  t —经过的时间(1)

Now let’s write this equation in Python…

现在让我们用Python编写这个方程式...

To test this function write a call using the parameters from above…

要测试此功能，请使用上面的参数编写调用…

108.29995068075098

Note: The resulting value is different and more accurate.

注意：结果值是不同的，并且更准确。

It’s worth mentioning that as the limit of the compounding frequency approaches infinity the higher the resulting amount in time-period t dollars.

值得一提的是，随着复合频率的极限接近无穷大，时间周期内的结果量也就越高。

108.29995068075098 # Compounding period of 12
108.31429591590663 # Compounding period of 24
108.31909221757883 # Compounding period of 36
108.32149310823426 # Compounding period of 48

The proof is outside the scope of this article but the result is an equation that compounds continuously. I the future I will discuss the importance of continuous compounding, trading, and time and their relation to higher-level model derivations including the Black-Scholes equation.

证明不在本文的讨论范围之内，但结果却是一个不断复杂化的方程式。 将来，我将讨论持续复利，交易和时间的重要性，以及它们与包括Black-Scholes方程在内的高级模型推导的关系。