A decision tree is a very important supervised learning technique. It is basically a classification problem. It is a tree-shaped diagram that is used to represent the course of action. It contains the nodes and leaf nodes. it uses these nodes and leaf nodes to draw the conclusion. Here we are going to talk about the entropy in the decision tree. Let’s have a look at what we are going to learn about the decision tree entropy.

决策树是一种非常重要的监督学习技术。 这基本上是一个分类问题。 它是一个树形图，用于表示操作过程。 它包含节点和叶节点。 它使用这些节点和叶节点来得出结论。 在这里，我们将讨论决策树中的熵。 让我们看一下我们将要学习的有关决策树熵的知识。

• What is Entropy?
  什么是熵？
• Importance of entropy.
  熵的重要性。
• How to calculate entropy?
  如何计算熵？

什么是熵？ (What is Entropy?)

So let’s start with the definition of entropy. What is this entropy?

因此，让我们从熵的定义开始。 这是什么熵？

“The entropy of a decision tree measures the purity of the splits.”

“决策树的熵衡量了拆分的纯度。”

Now let us understand the theory of this one-line definition. Let’s suppose that we have some attributes or features. Now between these features, you have to decides that which features you should use as the main node that is a parent node to start splitting your data. So for deciding which features you should use to split your tree we use the concept called entropy.

现在让我们了解这一单行定义的理论。 假设我们有一些属性或功能。 现在，在这些功能之间，您必须确定应使用哪些功能作为开始分裂数据的父节点的主节点。 因此，为了确定应使用哪些功能来分割树，我们使用了称为熵的概念。

熵的重要性 (Importance of Entropy)

1. It measures the impurity and disorder.
   它测量杂质和无序。
2. It is very helpful in decision tree to make decisions.
   在决策树中进行决策非常有帮助。
3. It helps to predict, which node is to split first on the basis of entropy values.
   它有助于根据熵值预测哪个节点首先分裂。

如何计算熵？ (How to calculate Entropy?)

Let’s first look at the formulas for calculating Entropy.

首先让我们看一下计算熵的公式。

Here, p is the Probability of positive class and q is the Probability of negative class.

在此，p是肯定类别的概率， q是否定类别的概率。

Now low let’s understand this formula with the help of an example. consider some features. Let’s say E1, E2, E3 are some features. we need to make a tree using one of the appropriate features as the parent node. let’s suppose that E2 is the parent node and E1, E3 are leaf node. Now when we construct a decision tree by considering E2 as parent node then it will look like as shown below.

现在低点，让我们借助示例来了解此公式。 考虑一些功能。 假设E1，E2，E3是一些功能。 我们需要使用适当的特征之一作为父节点来制作树。 假设E2是父节点，而E1，E3是叶节点。 现在，当我们通过将E2作为父节点来构建决策树时，其外观将如下所示。

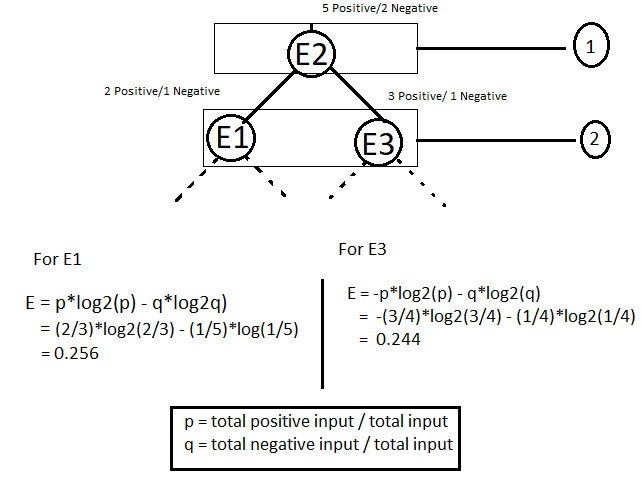
I have considered the E2 as a parent node which has 5 positive input and 2 negatives input. The E2 has been split into two leaf nodes (step 2). After the spilt, the data has divided in such a way that E1 contains 2 positive and1 negative and E3 contains 3 positive and 1 negative. Now in the next step, the entropy has been calculated for both the leaf E1 and E2 in order to find out that which one is to consider for next split. The node which has higher entropy value will be considered for the next split. The dashed line shows the further splits, meaning that the tree can be split with more leaf nodes.

我已经将E2视为具有5个正输入和2个负输入的父节点。 E2已被拆分为两个叶节点(步骤2)。 进行拆分后，数据以E1包含2个正值和1个负值以及E3包含3个正值和1个负值的方式进行了划分。 现在，在下一步中，已经为叶E1和E2都计算了熵，以找出下一步要考虑的熵。 具有较高熵值的节点将被考虑用于下一个分割。 虚线显示了进一步的拆分，这意味着可以用更多的叶节点拆分树。

N

ñ

NOTE 2: The value of entropy is always between 0 to 1.

注2：熵值始终在0到1之间。

So this was all about with respect to one node only. You should also know that for further splitting we required some more attribute to reach the leaf node. For this, there is a new concept called information gain.

因此，这仅涉及一个节点。 您还应该知道，为了进一步拆分，我们需要更多属性才能到达叶节点。 为此，有一个称为信息增益的新概念。

Worst Case:- If you are getting 50% of data as positive and 50% of the data as negative after the splitting, in that case the entropy value will be 1 and that will be considered as the worst case.

最坏的情况：-如果拆分后获得50％的数据为正，而50％的数据为负，则熵值将为1，这将被视为最坏情况。

If you like this post then please drop the comments and also share this post.

如果您喜欢此帖子，请删除评论并分享此帖子。