图像处理傅里叶变换图像变化
What do Fourier Transforms do? What do the Fourier modes represent? Why are Fourier Transforms notoriously popular for data compression? These are the questions this article aims to address using an interesting analogy to represent images.
傅立叶变换有什么作用? 傅立叶模式代表什么? 为什么众所周知,傅立叶变换在数据压缩方面很受欢迎? 这些是本文旨在使用有趣的类比表示图像来解决的问题。
Images are digital paintings. They are made up of different features. Some features require really precise control of the brush like drawing whiskers on a dog. Others can be quickly filled in with a thick brush, like a clear blue sky. All images are a combination of fine and dull features to varying degrees, i.e. high-frequency and low-frequency features.
图像是数字绘画。 它们由不同的功能组成。 一些功能需要真正精确地控制画笔,例如在狗上绘制胡须。 其他人可以用浓密的刷子快速填充,例如湛蓝的天空。 所有图像在不同程度上都是精细特征和暗淡特征的组合,即高频和低频特征。
let’s take a moment to understand how frequencies crept up into our analysis. Imagine the sine wave over half a period. It slowly goes up reaches a maximum and then slowly diminishes. The higher the frequency of the sine, the narrower the wave.
让我们花一点时间来了解频率是如何爬升到我们的分析中的。 想象一下半个周期的正弦波。 它缓慢上升达到最大值,然后缓慢减小。 正弦频率越高,波形越窄。

Imagine a cursed painter, who can only paint with brushes whose tips are half-wave sines. If he were to draw a delicately fine feature like the whiskers on a dog, he would choose a brush with a sine which has high frequency i.e. a narrowly pointed brush. Similarly, if he were to paint a clear sky that is devoid of any finer details, he would choose a brush with low frequency i.e. a fat thicker one.
想象一个被诅咒的画家,他只能用笔尖是半波正弦的画笔进行绘画。 如果要在狗身上画出细微的特征(如胡须),他会选择频率较高的正弦画笔,即窄尖的画笔。 同样,如果他要绘制没有任何精细细节的晴朗天空,则他会选择频率较低的画笔,即较厚的脂肪。
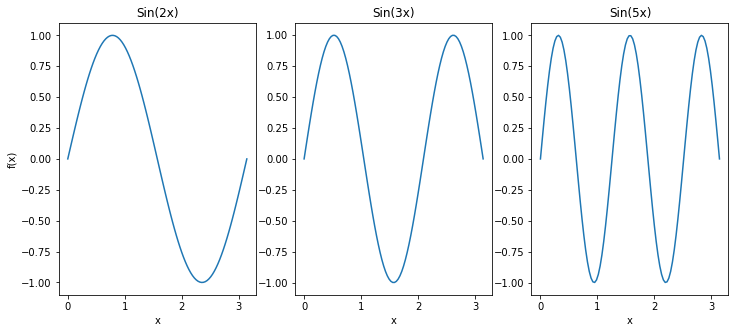
Surprisingly, all the images to ever exist are just like the artwork of the cursed painter. Notably, Fourier showed that every image (signal) can be decomposed into a range of sinuous terms where each term has a magnitude. The magnitudes are called Fourier coefficients. The whole process of decomposing an image into various sine terms and concomitantly their magnitudes is called Fourier decomposition. Fourier series is a much more general scenario, where the signals to be decomposed are periodic. Fourier Transforms are special cases where signals have an infinite time-period, i.e. non-periodic.
令人惊讶的是,所有存在的图像都像被诅咒的画家的作品一样。 值得注意的是,傅立叶(Fourier)表明,每个图像(信号)都可以分解为一系列正弦项,其中每个项都有一个大小。 幅度称为傅里叶系数。 将图像分解为各种正弦项及其幅度的整个过程称为傅里叶分解。 傅立叶级数是一种更为通用的方案,其中要分解的信号是周期性的。 傅立叶变换是信号具有无限时间周期(即非周期性)的特殊情况。
One elegant and fast algorithm to do the above decomposition is the Fast Fourier Transform, which is arguably the most important algorithm to be developed in the 21st century. It has far-reaching applications in cellular communications, satellites, films, televisions, and much more.
快速傅立叶变换是完成上述分解的一种优雅而快速的算法,它可以说是21世纪最重要的算法。 它在蜂窝通信,卫星,电影,电视等领域具有广泛的应用。
To visualize the sinuous nature of images, it would be interesting to plot the magnitude of an image as if it were a surface plot and observe the top view of the contours. This idea was developed by Dr. Steven Brunton at the University of Washington.
为了可视化图像的弯曲性质,将图像的大小绘制为表面图并观察轮廓的俯视图将很有趣。 这个想法是华盛顿大学的史蒂文·布伦顿博士提出的。
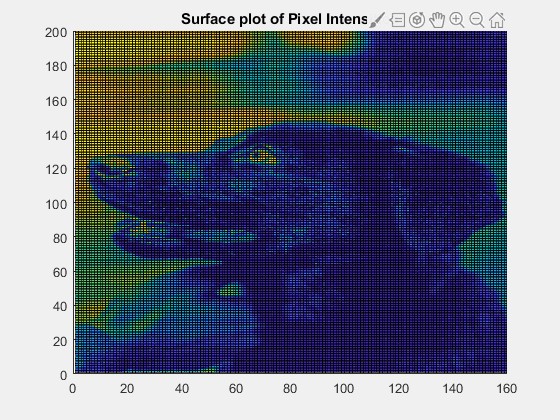
The sinuous nature of the image is clearly visible. the high-frequency features are sharply visible as narrow peaks. These include the eyes, the outlines of the facial structure, and the outline of the human hand. The low-frequency features, which are usually huge stretches of uniform color, are observed in the background. These include large regions of black colored fur and the background.
图像的弯曲性质清晰可见。 高频特征清晰可见为窄峰。 这些包括眼睛,面部结构轮廓和人手轮廓。 通常在背景中观察到低频特征,通常是巨大的均匀颜色延伸。 其中包括黑色毛皮和背景的大区域。
Here, is the simple code to replicate the prior results.
这是复制先前结果的简单代码。
The source code to animate the surface plot is included in my Github, here!
我的Github中包含了动画曲面图的源代码, 在这里 !
This is called as the bed sheet view of the image. The idea behind the name is that if four people were holding each side of a bedsheet and begin oscillating it at one of the Fourier frequency with the corresponding magnitude and a similar setup with four people exists for each of the infinite Fourier modes, then the superposition of all the bedsheets would result physically in creases which look like the above image. Hence, the name, bed sheet view!
这称为图像的床单视图。 该名称背后的想法是,如果四个人拿着床单的每一侧,并开始以相应的幅度以傅立叶频率之一进行振荡,并且对于每个无限傅立叶模式都存在四个人的相似设置,则该叠加所有的床单都会在物理上导致皱纹,看起来像上面的图像。 因此,名称,床单视图!
Okay, now that a good intuition is developed to understand what Fourier transforms can do, its a good exercise to go over these ideas formally. The Fourier decomposition equation for a discrete signal looks like:
好的,现在已经发展出一种很好的直觉来理解傅立叶变换可以做什么,这是一个很好的练习,可以正式地研究这些想法。 离散信号的傅立叶分解方程如下:
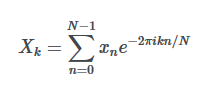
Here, xn is the value of the signal at time n. Xk is the Fourier coefficient for each frequency k. N is the total number of samples of the signal (i.e. the number of discrete time steps over which the signal was recorded). The FFT algorithm returns the Xk values for each frequency. The complex exponential can be decomposed into sines and cosines using the Euler’s formula. This provides a sanity check to the intuitions developed so far.
在此,xn是时间n处的信号值。 Xk是每个频率k的傅立叶系数。 N是信号采样的总数(即记录信号的离散时间步长)。 FFT算法返回每个频率的Xk值。 可以使用欧拉公式将复指数分解为正弦和余弦。 这为到目前为止开发的直觉提供了健全的检查。
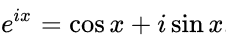
For example, let’s build a sinuous signal out of multiple frequencies. Say a combination of sines with 50, 100, and 200 hertz as frequencies and at different proportions. The periodic nature is still visible, but it is really hard to understand the original frequency components by visualizing the signal in the time domain.
例如,让我们从多个频率构建一个正弦信号。 说出频率分别为50、100和200赫兹的正弦组合。 周期性仍然是可见的,但是通过在时域中可视化信号很难理解原始频率分量。
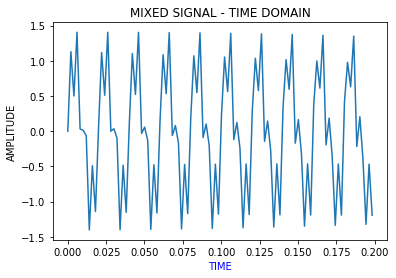
The Fourier Transform helps to intuitively visualize the signals in the frequency domain. So, applying the Fourier decomposition on the above signal gives us the following plot.
傅立叶变换有助于直观地可视化频域中的信号。 因此,对上述信号进行傅立叶分解可得出以下曲线。
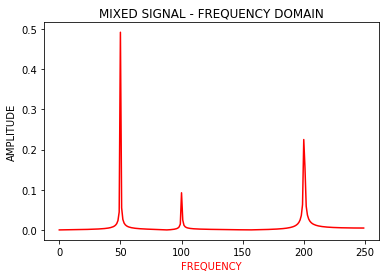
The true frequencies of the mixture at 50, 100, and 200 Hz show peaks in the frequency domain as expected. Notably, the FFT algorithm can also give the weightage of each frequency component, without having any prior knowledge of the signal.
混合物在50、100和200 Hz的真实频率如预期的那样在频域中显示出峰值。 值得注意的是,FFT算法还可以给出每个频率分量的权重,而无需事先了解信号。
Now going back to the bedsheet view of images, every picture is a 2-dimensional signal on which the Fourier decomposition can be applied. If a slice of the image is taken, it would resemble the time domain signal from our example, however with its own frequency components. The bedsheet views are powerful to develop intuition behind how an image can be a simple signal in the time domain, with multiple dimensions.
现在回到图像的床单视图,每张图片都是一个二维信号,可以对其进行傅立叶分解。 如果拍摄图像的一部分,它将类似于我们示例中的时域信号,但是具有自己的频率分量。 床单视图功能强大,可以直观地理解图像在时域中如何成为具有多个维度的简单信号。
In general, the information-dense regions are made up of high-frequency terms and plain stretches of uniformity are made up of lower frequency terms. The genius of Fourier is deriving the weighted modes (or frequency — magnitude pair). This gives an idea to understand the most important modes which make up the image. Turns out the Pareto rule holds true here and a really small number of modes contain most of the information about the image. This principle is crucial to data compression. By ignoring the majority of modes, we could reduce the size of the image. However, the quality of the image is only slightly compromised.
通常,信息密集区域由高频项组成,均匀性的平坦范围由低频项组成。 傅立叶的天才在于推导加权模式(或频率-幅度对)。 这给出了一个了解构成图像的最重要模式的想法。 事实证明,帕累托规则在这里成立,很少有模式包含有关图像的大多数信息。 该原理对于数据压缩至关重要。 通过忽略大多数模式,我们可以减小图像的大小。 但是,图像的质量只会略有下降。
If you are interested in going more in-depth on how Fourier Transforms are used for data compression, or to understand why data is compressible, to begin with, check out my previous article. As always, reach out to me to continue the conversation or provide me with some feedback on the content.
如果您想更深入地了解如何使用傅里叶变换进行数据压缩,或者想了解为什么数据是可压缩的,那么请阅读我的上一篇文章 。 与往常一样,请与我联系以继续对话或向我提供有关内容的反馈。
翻译自: https://towardsdatascience.com/fourier-transforms-and-bed-sheet-view-of-images-58ba34e6808a
图像处理傅里叶变换图像变化
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.mzph.cn/news/388587.shtml
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!



)











,R(查全率),F1值)


