声明 (Statement)

We have to search for a value x in a sorted matrix M. If x exists, then return its coordinates (i, j), else return (-1, -1).

我们必须在排序的矩阵M中搜索值x 。 如果x存在，则返回其坐标(i，j) ，否则返回(-1，-1) 。

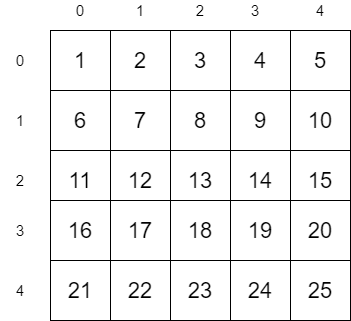
Let us consider the above matrix as an example. In this example, we are going to search for the value 12. Since 12 is present in the matrix, the algorithm should return its coordinates (2, 1)

让我们以上述矩阵为例。 在此示例中，我们将搜索值12。由于矩阵中存在12，因此算法应返回其坐标(2，1)

简单方法 (Simple Approach)

A simple approach is to traverse all the values in the matrix and check if it is equal to 12.

一种简单的方法是遍历矩阵中的所有值并检查其是否等于12。

The worst case time complexity of the above algorithm will be O(n x m) = O(n²) when n = m

当n = m时，上述算法的最坏情况下时间复杂度将为O(nxm)= O(n²)

高效方法 (Efficient Approach)

The above algorithm behaves worse for large values of n and m. Let us look into the efficient algorithm now.

对于较大的n和m值，上述算法的性能较差。 现在让我们研究高效算法。

算法 (Algorithm)

1. Start from Top Right position (0, m - 1) in the matrix M2. If the value is equal to x return (0, m - 1)3. Move one row down if the current value is less than x4. Move one column left if the current value is greater than x

Let us apply this algorithm into our matrix M. We are going to search for the value 12 in M

让我们将此算法应用到矩阵M中。我们将在M中搜索值12

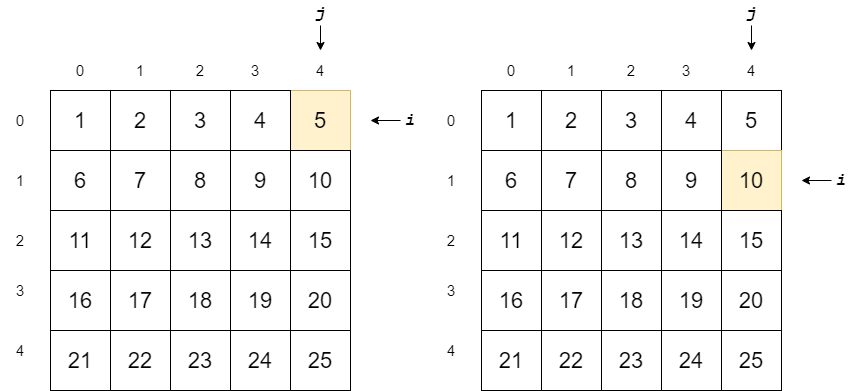
1. Start from the Top Right value 5 at M[0][4]. 5 is less than 12, so 12 should be somewhere in the bottom of the matrix since all row and column values are sorted in ascending order. So we move one row down.

   从M [0] [4]的右上角值5开始。 5小于12，因此12应该在矩阵底部的某个位置，因为所有行和列值都按升序排序。 因此，我们向下移动了一行。

2. The value 10 at M[1][4] is also less than 12, so we move one row down.

   M [1] [4]上的值10也小于12，因此我们向下移动了一行。

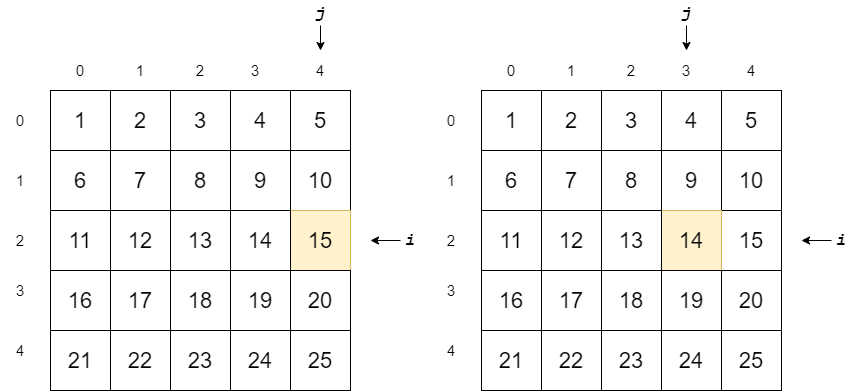
3. The value 15 at M[2][4] is greater than 12, so 12 should be somewhere in the left of the matrix, so we move one column left.

3. M [2] [4]上的值15大于12，因此12应该在矩阵的左侧某处，因此我们向左移动一列。

4. The value 14 at M[2][3] is also greater than 12, so we move one column left

4. M [2] [3]上的值14也大于12，因此我们向左移动一列

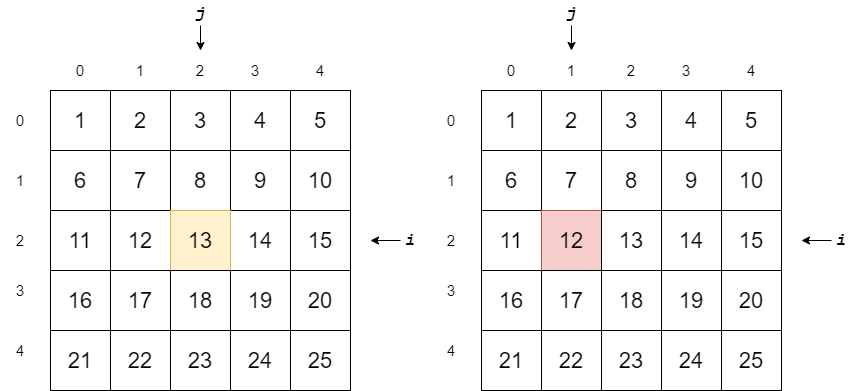
5. The value 13 at M[2][2] is greater than 12, so we move one column left

5. M [2] [2]的值13大于12，所以我们向左移动一列

6. The value at M[2][1] is equal to 12, so we return its index (2, 1)

6. M [2] [1]处的值等于12，因此我们返回其索引(2，1)

The worst case time complexity of the above algorithm will be O(n + m) = O(2n) = O(n) when n = m, because we will be iterating all rows and all columns once if x is at the bottom left position (n - 1, 0)

当n = m时，上述算法的最坏情况下时间复杂度将为O(n + m)= O(2n)= O(n) ， 因为如果 x 位于左下角 ， 我们将对所有行和所有列进行一次迭代 位置 (n-1，0)

You can find the Java solution for this algorithm in the Github repo.

您可以在Github存储库中找到该算法的Java解决方案。

谢谢🙏 (Thank you 🙏 👋🤘)

Linkedin | Github

Linkedin | Github