Let’s explore one of the simplest datasets, The IRIS Dataset which basically is a data about three species of a Flower type in form of its sepal length, sepal width, petal length, and petal width. The data set consists of 50 samples from each of the three species of Iris (Iris setosa, Iris virginica, and Iris versicolor). Four features were measured from each sample: the length and the width of the sepals and petals, in centimeters. Our objective is to classify a new flower as belonging to one of the 3 classes given the 4 features.

让我们探索最简单的数据集之一，IRIS数据集，该数据集基本上是有关花类型的三种物种的数据，其形式为萼片长度，萼片宽度，花瓣长度和花瓣宽度。 所述数据集包括从每三个物种鸢尾的50个样品( 山鸢尾 ， 虹膜锦葵 ，和变色鸢尾 )。 从每个样品中测量出四个特征： 萼片和花瓣的长度和宽度，以厘米为单位。 我们的目标是根据4个特征将新花归为3类之一。

Download IRIS data from here.

从此处下载IRIS数据。

Here I'm importing the libraries in ipython notebook using Anaconda Navigator(download: https://www.anaconda.com/products/individual). which can be useful in our exploratory data analysis like pandas, matplotlib, numpy and seaborn.

在这里，我使用Anaconda Navigator(下载： https ://www.anaconda.com/products/individual)在ipython Notebook中导入库。 这对我们的探索性数据分析(如熊猫 ， matplotlib ， numpy和seaborn)很有用 。

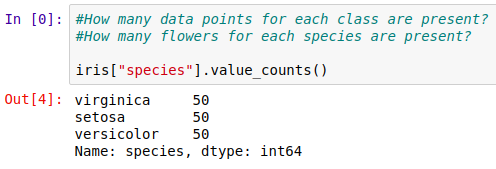
Here, IRIS is a balanced dataset because the number of data points for every class Setosa, Virginica, and Versicolor is 50. If the classes are having the different numbers of data points each then it’s an imbalanced dataset.

在这里，IRIS是一个平衡的数据集，因为Setosa，Virginica和Versicolor每个类的数据点数均为50。如果每个类的数据点数均不同，则它是一个不平衡的数据集。

2D散点图 (2D Scatter Plot)

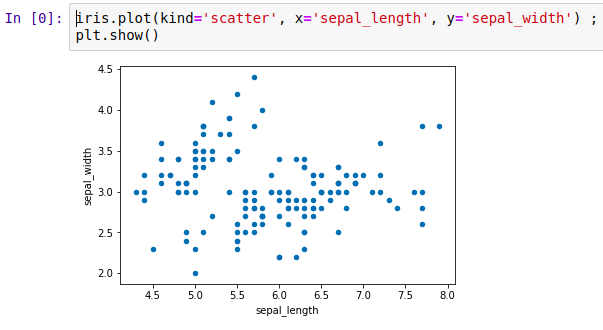
By using the pandas object we created before we can plot a simple 2D graph of the features we give as x and y parameters of the plot() method of pandas. Matplotlib method show() helps to actually plot the data.

通过使用我们创建的pandas对象，我们可以绘制简单的二维图形来绘制作为pandas plot()方法的x和y参数的要素。 Matplotlib方法show()有助于实际绘制数据。

But by Seaborn we can plot a more informative graph by color-coding by each flower type.

但是通过Seaborn，我们可以通过每种花的颜色编码来绘制更具信息量的图。

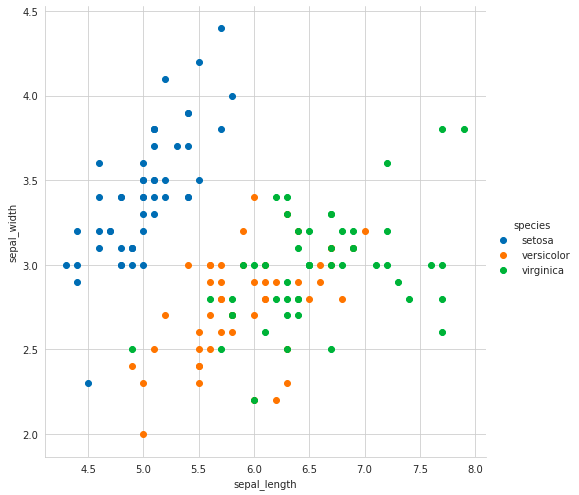
Here in the above graph notice that Blue Setosa points can be easily separated from Orange Versicolor and Green Verginica points by simply drawing a line but the Orange and Green points are still complex to be separated because they are overlapping. So by using sepal_length and sepal_width features of the data we can get this much information.

在上图中，通过简单画一条线可以很容易地将Blue Setosa点与Orange Versicolor点和Green Verginica点分离，但是Orange点和Green点由于重叠而仍然很复杂，难以分离。 因此，通过使用数据的sepal_length和sepal_width功能，我们可以获得很多信息。

2D散点图：对图 (2D Scatter Plot: Pair Plot)

Pair Plot by Seaborn is capable of drawing multiple 2D Scatter Plots for each possible combination of features in one go.

Seaborn的结对图能够一次性绘制多个2D散点图，以用于每种可能的特征组合。

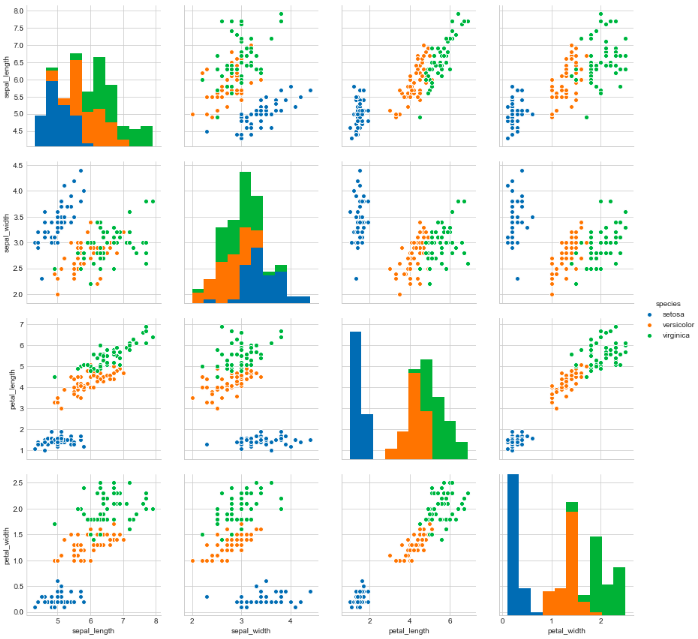
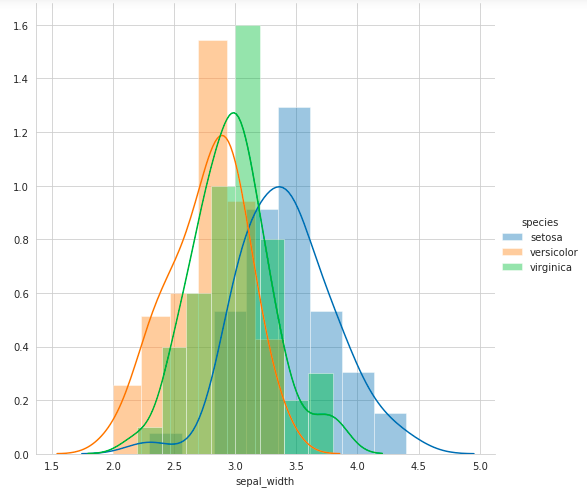
So here if we observe the pair plots then we can say petal_length and petal_width are the most essential features to identify various flower types. While Setosa can be easily linearly separable, Virnica and Versicolor have some overlap. So we can separate them by a line and some “if-else” conditions.

因此，在这里，如果我们观察对图，那么我们可以说花瓣长度和花瓣宽度是识别各种花朵类型的最基本特征。 虽然Setosa可以很容易地线性分离，但Virnica和Versicolor有一些重叠。 因此，我们可以通过一行和一些“ if-else”条件将它们分开。

一维散点图，直方图，PDF和CDF (1D Scatter Plot, Histogram, PDF & CDF)

As we can observe the graph, it's very hard to make sense as points are overlapping a lot. There are better ways to visualize the scatter plots. By Seaborn, we can plot a Probability Distribution Function cum Histogram.

正如我们可以观察到的图形一样，由于点重叠很多，很难理解。 有更好的方法可视化散点图。 通过Seaborn，我们可以绘制概率分布函数和直方图 。

Histogram : Histogram is the plot representing the frequency counts of each data window of the feature for which the plot is drawn (Bar shapes in the graph).

直方图 ：直方图是表示绘制该图的要素的每个数据窗口的频率计数的图(图中的条形)。

PDF : Probability Density Function is basically a smoothed histogram. Every point on the PDF represents the probability for that particular value in the data (bell shaped curve in the graph). PDF gets formatted using Kernel Density Estimation. For each value of the point on x-axis, y-axis value represents its probabily of occuring in the dataset. More the y value more of that value exists in the dataset.

PDF ： 概率密度函数基本上是平滑的直方图。 PDF上的每个点都代表数据中该特定值(图中的钟形曲线)的概率。 使用内核密度估计来格式化PDF。 对于x轴上每个点的值，y轴值表示其在数据集中出现的概率。 y值越大，数据集中存在的值越多。

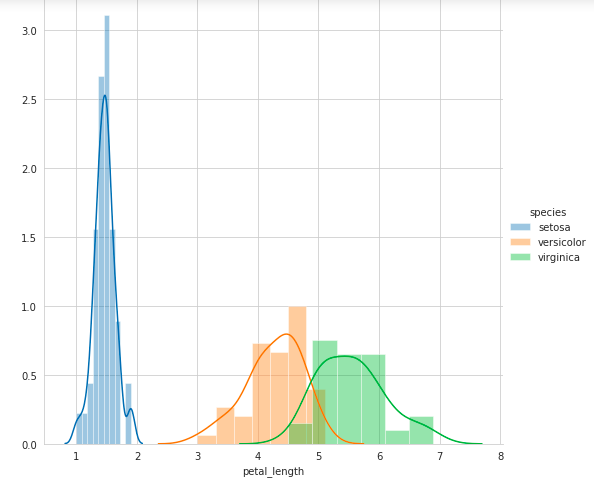
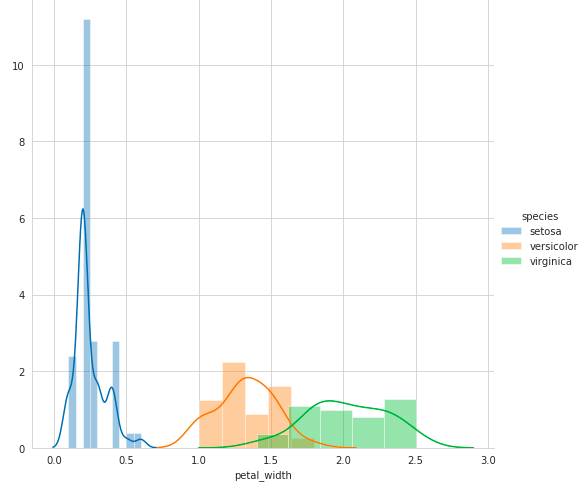
Now from these graphs, we can observe that by using just one feature a simple model can be formed by if..else condition as if(petal_length) < 2.5 then flower type is Setosa.

现在从这些图形中，我们可以观察到，仅使用一个功能，就可以通过if..else条件( if(petal_length)<2.5)形成简单模型， 然后花朵类型为Setosa 。

Now, what if we need the percentage of Versicolor points having a petal_length of less than 5 ? here comes CDF in our rescue!

现在，如果我们需要花瓣长度小于5的Versicolor点的百分比呢？ CDF来了！

CDF: Cumulative Density Function is the cumulative sum of the PDF. Every point on the CDF curve represents integration of the PDF till that point of CDF. Below is the histogram of the Yield. Every point on the CDF represents how much percentage of the total points belong to below that point.

CDF：累积密度函数是PDF的累积和。 CDF曲线上的每个点都代表PDF到CDF为止的积分。 以下是收益的直方图。 CDF上的每个点代表该点以下的总点数百分比。

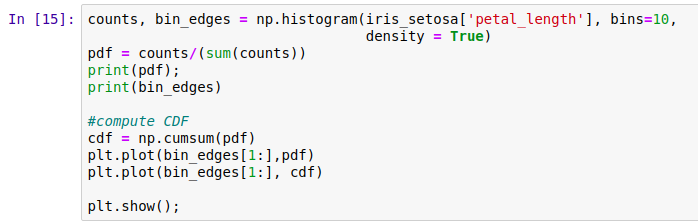
To construct a histogram, the first step is to “bin” the range of values — that is, divide the entire range of values into a series of intervals — and then count how many values fall into each interval. The bins are usually specified as consecutive, non-overlapping intervals of a variable. The bins (intervals) must be adjacent and are often (but are not required to be) of equal size(for more information: https://www.datacamp.com/community/tutorials/histograms-matplotlib).

要构建直方图，第一步是将值的范围“ bin”(即，将值的整个范围划分为一系列间隔)，然后计算每个间隔中有多少值。 通常将bin指定为变量的连续，不重叠的间隔。 垃圾箱(间隔)必须相邻，并且经常(但不是必须)大小相等(有关更多信息，请访问： https : //www.datacamp.com/community/tutorials/histograms-matplotlib )。

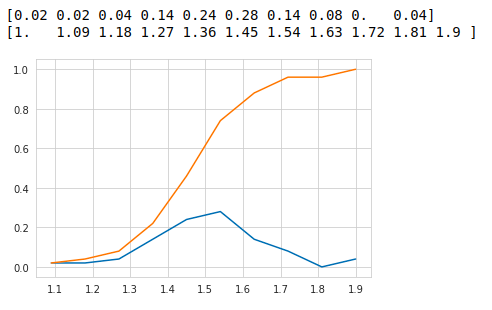
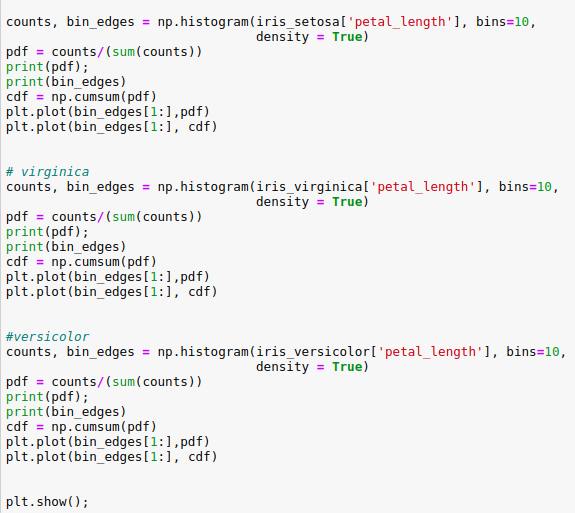
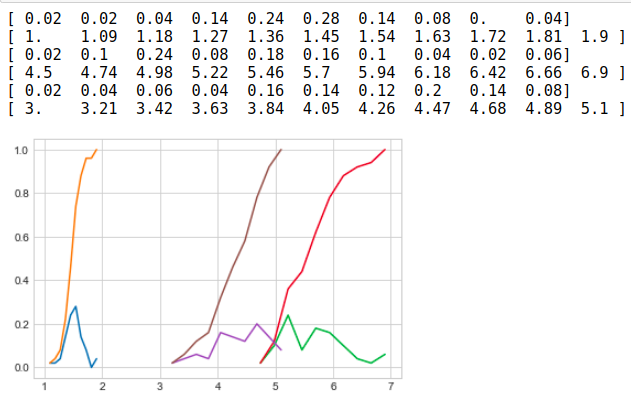
Now by plotting of CDF of petal_length for various types of flowers in a combined manner we can get an overall picture of the data.

现在，通过组合绘制各种类型花朵的petlet_length的CDF，可以得到数据的整体图。

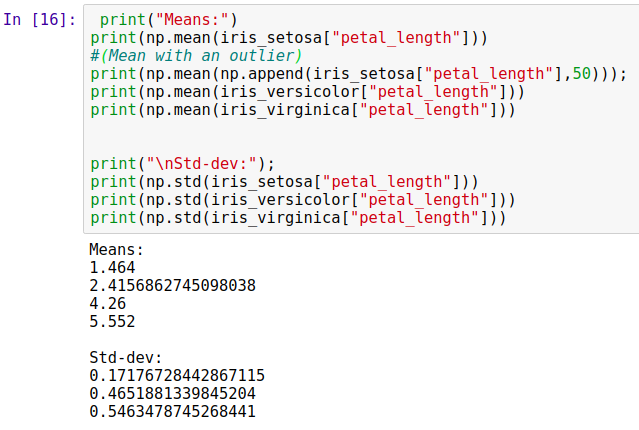
Mean, Variance and Standard Deviation

均值，方差和标准差

Mean: https://en.wikipedia.org/wiki/Mean

意思是： https : //en.wikipedia.org/wiki/Mean

Variance: https://en.wikipedia.org/wiki/Variance

差异： https ： //en.wikipedia.org/wiki/Variance

Standard Deviation: https://en.wikipedia.org/wiki/Standard_deviation

标准偏差： https ： //en.wikipedia.org/wiki/Standard_deviation

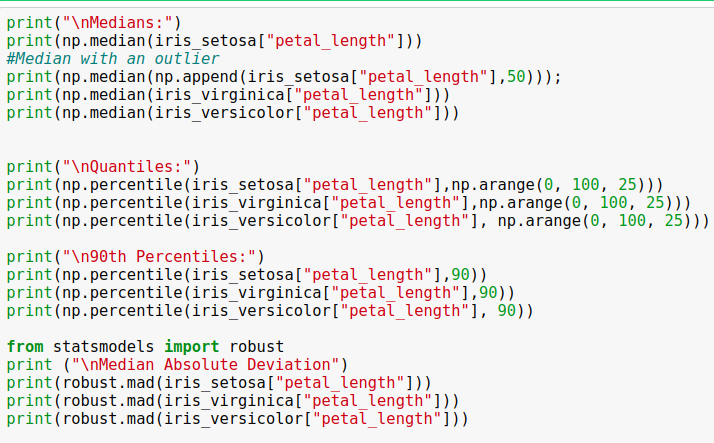
Median, Percentile, Quantile, MAD, IQR

中位数，百分位数，分位数，MAD，IQR

Median: https://en.wikipedia.org/wiki/Median

中位数： https ： //en.wikipedia.org/wiki/Median

Percentile: https://en.wikipedia.org/wiki/Percentile

百分位数： https : //en.wikipedia.org/wiki/Percentile

Quantile: https://en.wikipedia.org/wiki/Quantile

分位数： https : //en.wikipedia.org/wiki/Quantile

MAD: Median Absolute Deviation: https://en.wikipedia.org/wiki/Median_absolute_deviation

MAD：中位数绝对偏差： https ： //en.wikipedia.org/wiki/Median_absolute_deviation

IQR: Interquantile Range: https://en.wikipedia.org/wiki/Interquartile_range

IQR：分位数范围： https ：//en.wikipedia.org/wiki/Interquartile_range

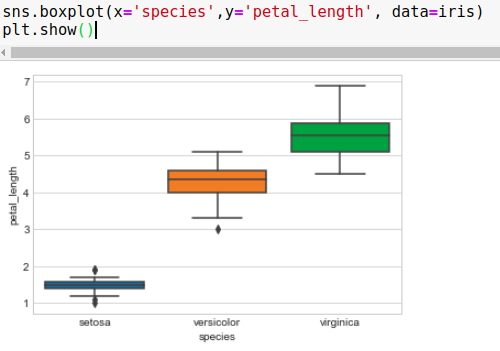
箱形图 (Box Plots)

Box plots with whiskers is another method for visualizing the 1D Scatter Plot more intuitively. The boxes in the graph represent Interquantile Range as the first horizontal line from the bottom of the box represents 25th percentile value, the middle line represents the 50th percentile and the top line represents the 75th percentile. The black lines outside of the boxes are called whiskers. It’s not fixed what whiskers represent but it might be the minimum value of the feature at below horizontal line and maximum value at the top horizontal line in some cases.

带晶须的箱形图是另一种更直观地可视化1D散布图的方法。 图中的框代表分位数范围，因为从框底部开始的第一条水平线代表第25个百分位数，中线代表第50个百分位数，顶线代表第75个百分位数。 盒子外面的黑线称为晶须。 晶须代表什么并不确定，但在某些情况下可能是特征在水平线以下的最小值和在水平线顶部的最大值。

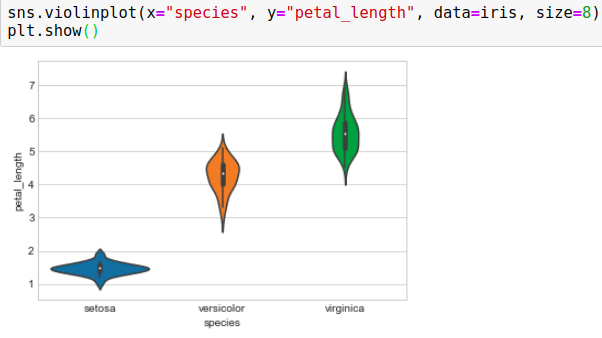
小提琴图 (Violin Plots)

Violin plot by Seaborn combine PDF and Box-Plot. As in the below plot, on all three colors, PDFs of petal_length are on the sides of the shape, and in the center in black, there is a representation of Box-Plots.

Seaborn的小提琴图结合了PDF和Box-Plot。 如下图所示，在所有三种颜色上，petlet_length的PDF都位于形状的侧面，而黑色的中心则是Box-Plots的表示形式。

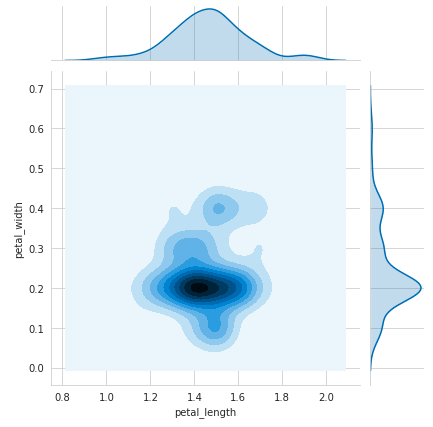
多元概率密度：轮廓图 (Multivariate Probability Density: Contour Plot)

Seaborn provides jointplot() method for contours. The name is “jointplot” because it represents Contours as well as PDFs on the edges. More the darker the region the more the probability of occurring that value of features for which the graph is plotted.

Seaborn提供了用于轮廓的jointplot()方法。 名称为“ jointplot”，因为它表示轮廓以及边缘的PDF 。 区域越黑，绘制该图的要素的值出现的可能性就越大。