关联分析（Association analysis）

简介

大量数据中隐藏的关系可以以‘关联规则’和‘频繁项集’的形式表示。rules：｛Diapers｝–>{Beer}说明两者之间有很强的关系，购买Diapers的消费者通常会购买Beer。
除了应用在市场篮子数据（market basket data）中，关联分析（association analysis）也可以应用在其他领域像bioinfomatic（分析复杂生物知识的学科）、medical diagnosis、Web mining和scientific data analysis。
在关联分析中有两个问题需要解决：1，从大量交易数据中发现隐藏的模式需要大量运算；2，有些模式可能只是刚好发生，因此这些模式是虚假的。所以以下内容包括两点：1，利用某种算法高效的挖掘这种模式；2，通过评估这些模式避免产生虚假结果。1
下面以market basket data分析为例：
这里写图片描述

几个概念：

Itemset
令I=i1,i2,⋯,id是所有项的集合。在association analysis中，0或更多项的集合称为itemset,具有k项的itemset称为k-itemset。
support count
包含某个特定的Itemset的交易数目。在表6.1中2-itemset｛Bread,Milk｝的support count:σ({Bread,Milk})=3(1)
rule
规则，不难理解，X→Y(X∩Y=∅)，箭头左边称为先决条件（antecedent），箭头右边称为结果（consequent）
support
某一项集或规则发生次数占总交易次数的百分比。s(X→Y)=s({X,Y})=σ(X∪Y)N(2)
例如：项集{Bread,Milk}的support为35
confidence
X发生时Y发生的概率，也即条件概率。
Confidence,c(X→Y)=σ(X∪Y)σ(X)(3)

寻找关联规则的两个步骤

给定一个交易集合T，寻找所有的满足support≥minsup，并且confidence≥minconf的规则，minsup和minconf是相应的support和confidence的阈值。
一种寻找关联规则的方法是计算每一条可能规则的support和confidence，也就是我们说的蛮力法。这种方法需要大量的运算，因为规则的个数是呈指数增长的。一个包含d个项的数据集可以提取出的规则的数目是

R = 3 d - 2 d + 1 + 1 (自 己 证 明 ？)

既然我们不想使用蛮力法，那么应该使用什么方法来寻找关联规则呢？从上式(1)可以看出规则

X→Y 的support仅仅依赖于相应的项集

X∪Y 的support。例如，下面的规则的support完全相同，因为他们有相同的项集{Beer,Diapers,Milk}:
{Beer,Diapers}

→ {Milk}，{Beer,Milk}

→ {Diapers}，{Diapers,Milk}

→ {Beer}，{Beer}

→ {Diapers,Milk}，{Milk}

→ {Beer,Diapers}，{Diapers}

→ {Beer,Milk}
如果项集{Beer,Diapers,Milk}不是频繁的，那么可以直接裁剪掉以上所有6个候选规则。
因此，许多关联规则挖掘算法将这个问题分解成两个主要子任务：
- 产生频繁项集：寻找所有达到support阈值的项集。
- 产生规则：从频繁项集中提取具有高置信度的规则，这些规则称为强规则。 2

产生频繁项集

Apriori原理

我们可以使用枚举法列举出所有可能的k-itemset，然后计算每个项集的support。一个具有m项的数据集可以产生2m−1个项集，而其中满足support阈值的项集可能很少。显然，当数据集很大时，枚举法并不是个高效的方法。从下图可以看出，有4个项的数据集，共有15个项集。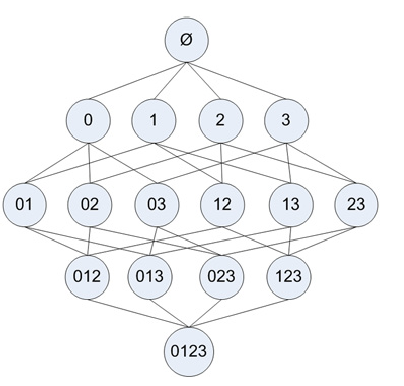
图来自机器学习实战
为了提高寻找频繁项集的效率，我们应该把那些不可能满足support阈值的项集裁剪掉。
Apriori原理：如果一个项集是频繁的，那么它的子项集也一定是频繁的
反过来说，如果一个项集不是频繁的，那么它的父项集也一定不是频繁的。下图加了阴影的项集被裁剪掉。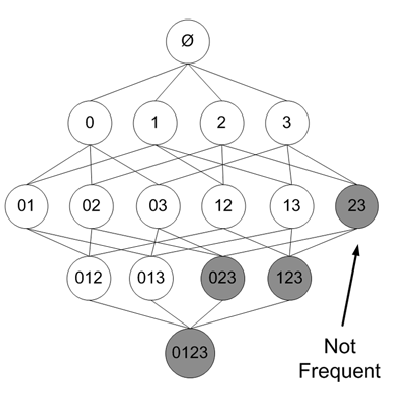
这里写图片描述
来自机器学习实战
根据以上原理，我们可以从上往下寻找频繁项集。也就是，首先寻找频繁项集：1-itemset，然后再由1-itemset组合成2-itemset…..（其实上图的例子并没有减少需要计算support的项集个数（这个是不是程序需要改进？？怎么只有1-itemset是infrequent的时候才能减少需要计算的项集数），如果 3 是infrequent的，那么以下包含3的项集可以全部忽略）
伪代码
1. 计算得到频繁项集1-itemset的集合:Ii，i=1
2. k=2
当 kle项的个数N时：
Ik=generateIk(D,Ii) …从I_i中产生频繁项集的集合Ii+1
i=k,k++

其中，generateIk函数是从k-itemset产生(k+1)-itemset
这个函数包含两个过程：连接和筛选。
- 连接
当确定了一个频繁项集k-itemset的全部集合后，它需要和自身连接，生成k+1-itemset。所谓连接，就是两个不同的频繁项集k-itemset，当它们的前（k-1）项都相同时，就进行合并。
- 筛选
从上面的定理我们得知，当子项不是频繁项集时，父项也一定不是频繁项集。但当子项都是频繁项集时，其父项却不一定是频繁项集。因此，在连接得到(k+1)-itemset后，还需要计算它的support，如果不满足support的阈值，那么就删去。

python程序

下面的程序和机器学习实战中的程序思想基本相同，但我个人感觉书中的程序有些难以理解，因此自己写了一个。感谢机器学习实战作者

'''产生频繁项集'''
def genFreqItemset(dataSet,minSupp=0.5):'''input:dataSet:training data,type:listoutput:freqSet:a list of all the k-itemset.each element is frozensetsupport:a dict,the support of frequent itemset'''unique_value={}I1=[]support={}freqSet=[]m=len(dataSet)for tran in dataSet:for item in tran:if item not in unique_value.keys():unique_value[item]=0unique_value[item]+=1for item in unique_value.keys():supp=float(unique_value[item])/mif supp>=minSupp:I1.append(frozenset([item]))  #frozeset can serve as a key to dictionarysupport[frozenset([item])]=supp #only record the support of frequent itemsetI1.sort();freqSet.append(I1)k=2Lk=[]while k<=m:Lk=generateLk(freqSet[k-2],k)Lk,LkSupp=filterLk(dataSet,Lk,minSupp)freqSet.append(Lk)support.update(LkSupp)k+=1return freqSet,supportdef generateLk(freq,k):'''input:freq:  the itemset in freq is k-1 itemsetk:  create k-itemset from k-1_itemsetoutput:Lk:a list of k-itemset,frequent and infrequent'''Lk=[]for i in range(0,len(freq)-1):for j in range(i+1,len(freq)):if list(freq[i])[0:k-2]==list(freq[j])[0:k-2]:#fore k-1 item is identityLk.append(frozenset(freq[i]|freq[j]))return Lkdef filterLk(dataSet,Lk,minSupp=0.5):'''input:  Lk: all the k-itemset that need to be prunedoutput:filteredLk: frequent k-itemset which satisfy the minimum supportLkSupp: the support of frequent k-itemset'''LkSupp={}filteredLk=[]for itemset in Lk:supp=calcSupport(dataSet,itemset)if supp>=minSupp:LkSupp[frozenset(itemset)]=suppfilteredLk.append(frozenset(itemset))return filteredLk,LkSuppdef calcSupport(dataSet,Lk):'''calculate the support of Lk,Lk is a frozenset'''# Lk=list(Lk)[0]dataSet=map(set,dataSet)m=len(dataSet)num=0for tran in dataSet:if Lk.issubset(tran):num+=1return float(num)/m

测试

>>> dataSet
[[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]
>>> Lk,support=apriori_f.genFreqItemset(dataSet,0.5)
>>> Lk[0]
[frozenset([1]), frozenset([2]), frozenset([3]), frozenset([5])]
>>> Lk[1]
[frozenset([1, 3]), frozenset([2, 3]), frozenset([2, 5]), frozenset([3, 5])]
>>> Lk[2]
[frozenset([2, 3, 5])]
>>> Lk[3]
[]
>>> support
{frozenset([5]): 0.75, frozenset([3]): 0.75, frozenset([2, 3, 5]): 0.5, frozenset([3, 5]): 0.5, frozenset([2, 3]): 0.5, frozenset([2, 5]): 0.75, frozenset([1]): 0.5, frozenset([1, 3]): 0.5, frozenset([2]): 0.75}

从频繁项集中提取强规则

修剪

从频繁项集中提取规则保证了这些规则的support一定满足minsupport，接下来就是置信度的计算。同样，我们可以使用蛮力列举所有可能的规则，并计算其置信度，但这样我们会做许多无用功。一个包含n项的频繁项集，可能产生的规则数是2n−1（自己证明）。
为了提高效率，我们采用同前面Apriori算法类似的裁剪方法：
如果X→Y−X不满足最小置信度，那么X′→Y−X′(X′⊆X)也一定不满足最小置信度。
证明：c(X→Y−X)=support(Y)support(X)<minConfidence
c(X′→Y−X′)=support(Y)support(X′)，其中，support(X′)≥support(X)，所以有c(X′→Y−X′)<minConfidence
如下图：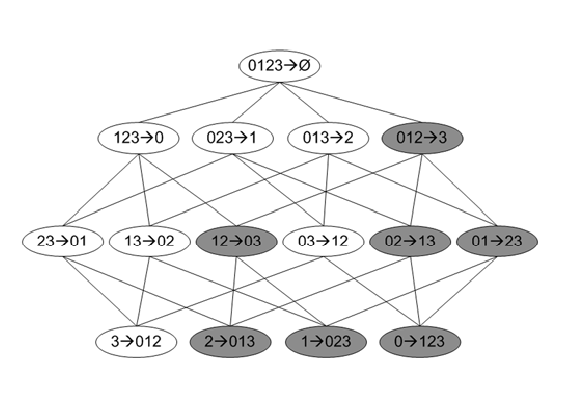
这里写图片描述
图中添加阴影的规则全部被裁剪掉。

python程序

def getBigRule(freq,support,minConf=0.5):'''input:  freq   : the frequent k-itemset,k=1,2,...nsupport:  corresponding support  outpur:bigRuleList: a list of all the rule that satisfy min confidence'''bigRuleList=[]m=len(freq)for i in range(1,m):genRules(freq[i],support,bigRuleList,minConf)return bigRuleListdef genRules(freq,support,brl,minConf=0.5):'''extract rules that satisfy min confidence from a list of k-itemset(k>1)put the eligible rules in the brl'''if len(freq)==0:returnif len(freq[0])==2: #handle 2-itemsetfor itemset in freq:for conseq in itemset:conseq=frozenset([conseq])conf=support[itemset]/support[itemset-conseq]if conf>=minConf:print itemset-conseq, '-->',conseq,'conf:',confbrl.append((itemset-conseq,conseq,conf))elif len(freq[0])>2:H=[]for itemset in freq:# first generate 1-consequence listfor conseq in itemset:conseq=frozenset([conseq])conf=support[itemset]/support[itemset-conseq]if conf>=minConf:print itemset-conseq, '-->',conseq,'conf:',confbrl.append((itemset-conseq,conseq,conf))H.append(conseq)m=2#  generate 2,...,k-1 consequencewhile m<len(freq[0]):H=generateLk(H,m)for conseq in H:conf=support[itemset]/support[itemset-conseq]if conf>=minConf:print itemset-conseq, '-->',conseq,'conf:',confbrl.append((itemset-conseq,conseq,conf))m+=1

利用以上得到的频繁项集测试：

>>> brl=apriori_f.getBigRule(freqSet,support,0.7)
frozenset([1]) --> frozenset([3]) conf: 1.0
frozenset([5]) --> frozenset([2]) conf: 1.0
frozenset([2]) --> frozenset([5]) conf: 1.0
frozenset([3, 5]) --> frozenset([2]) conf: 1.0
frozenset([2, 3]) --> frozenset([5]) conf: 1.0
>>> brl
[(frozenset([1]), frozenset([3]), 1.0), (frozenset([5]), frozenset([2]), 1.0), (frozenset([2]), frozenset([5]), 1.0), (frozenset([3, 5]), frozenset([2]), 1.0), (frozenset([2, 3]), frozenset([5]), 1.0)]