第五章 数组 和 广义表

数组和广义表可以看成是线性表在下述含义上的扩展：表中的数据元素本身也是一个数据结构。

 

5.1 数组的定义

n维数组中每个元素都受着n个关系的约束，每个元素都有一个直接后继元素。

可以把二维数组看成是这样一个定长线性表：它的每个数据元素也是一个定长线性表。

数组一旦定义，它的维数和维界就不再改变。因此，除了结构的初始化和销毁之外，数组只能有存取元素和修改元素值的操作。

 

5.2 数组的顺序表示和实现

次序约定：

1、列序为主序 column major order  FORTRAN

2、行序为主序 row major order     C

 

假设每个数据元素占L个存储单元，则二维数组A中的任一元素aij的存储位置可由下式确定：

LOC(i,j) = LOC(0,0) + (b2 * i + j)*L

LOC(i,j)是存储位置  LOC(0,0)称为基地址或基址

 

n维数组定位公式

Array[b1][b2]...[bn]

LOC(j1,j2,...,jn) = LOC(0,0,...,0) + (jn +jn-1*bn+jn-2*bn-1*bn + ... +j2*b3*...*bn +j1*b2*...*bn)*L

 

数组元素的存储位置是其下标的线性函数。

由于计算各个元素存储位置的时间相等，所以存取数组中任一元素的时间也相等，称具有这一特点的存储结构为随机存储结构。

    

5.3 矩阵的压缩

如何存储矩阵的元，使矩阵的各种运算能有效的进行。

二维数组可以存储矩阵的元。

有的程序设计语言中还提供了各种矩阵运算。

 

压缩存储：为多个值相同的元只分配一个存储空间；对零元不分配空间。

应用压缩的两种情况：

1、特殊矩阵：值相同的元素或者零元素在矩阵中的分布有一定规律；

2、稀疏矩阵。

 

对称矩阵：aij= aji  1 <= i,j <= n 称为n阶对称矩阵

可以为每一对对称元分配一个存储空间，即将n2个元压缩存储到n(n+1)/2个元空间中

以行序为主序，存储其下三角。

以一维数组sa[n(n+1)/2]作为n阶对称矩阵A的存储结构，则sa[k]和矩阵元aij之间存在一一对应的关系：

K = 

i(i - 1)/2 - 1 + j  当i>=j

j(j - 1)/2 - 1 + i  当i < j  //下标谁大谁除2，一维大是下三角内容，二维大是上三角内容

以上存法同样适用于三角矩阵。

 

三角矩阵：上/下三角中的元均为常数c或0的n阶矩阵（不含对角线）。

除了和对称矩阵一样，只存储其上/下三角中的元之外，再加一个存储常数c的存储空间即可。

对角矩阵：所有非零元集中在以主对角线为中心的带状区域中。即除了主对角线上和直接在对角线上、下方若干条对角线上的元之外，所有其他的元皆为零。

 

以上特殊矩阵，非零元的分布都有一个明显的规律，从而可以将其压缩存储到一维数组中，并找到每个非零元在一维数组中的对应关系。

 

稀疏矩阵：非零元较零元少，而且分布没有一定规律。

稀疏因子：矩阵中非零元个数与全部个数之比。

通常认为稀疏因子小于等于0.05时称为稀疏矩阵。

按照压缩存储的概念，只存储稀疏矩阵的非零元。

稀疏矩阵可由表示非零元的三元组 及其行列数唯一确定。

 

三种数据结构：三元组顺序表、行逻辑链接的顺序表、十字链表

1、三元组顺序表：以行序为主序顺序排列。

转置算法：

1、将矩阵的行列值相互交换；

2、将每个三元组中的i和j相互调换；

3、重排三元组之间的次序；

方法一：找到原矩阵的列序来进行转置。为了找到M的每一列中所有的非零元素，需要对其三元组表从第一行起整个扫描一遍。O（列数*非零元数）

方法二：先求出原矩阵每一列中非零元的个数，进而求得每一列第一个非零元在转置矩阵中应有的位置。 O（列数+ 非零元数）

三元组顺序表，又称为有序的双下标法。

特点：非零元在表中按行序有序存储，便于进行依行顺序处理的矩阵运算。

若需按行号存取某一行的非零元，则需从头开始进行查找。

2、行逻辑链接的顺序表：

在三元组顺序表的基础上，加入指示各行第一个非零元的顺序表。

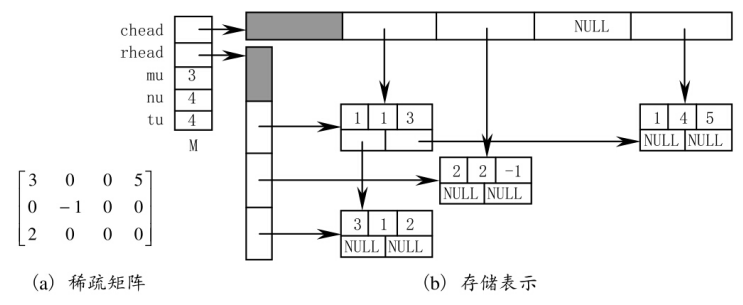
3、十字链表：

可以按任意顺序输入非零元素。

链式存储结构，每个非零元用一个含5个域的结点表示，其中i、j、e分别表示该非零元所在的行、列和非零元的值，向右域right链接同一行中下一个非零元，向下域down链接同一列中下一个非零元。

同一行的非零元通过right域链接成一个线性链表，

同一列的非零元通过down域链接成一个线性链表，

每个非零元即是某个行链表中的一个结点，又是某个列链表中的一个结点整个矩阵构成一个十字交叉的链表。

用两个分别存储行链表的头指针和列链表的头指针的一维数组表示十字链表。

 

矩阵加法：4种情况：

（1）aij+ bij 

（2）aij  插入元素

（3）bij   插入元素

（4）aij+ bij = 0 删除元素

 

从一个结点看，进行比较、修改指针所需的时间是一个常数；

整个运算过程是对A和B的十字链表逐行扫描，其循环次数主要取决于A和B矩阵中非零元素的个数ta和tb，由此算法时间复杂度为O(ta + tb)。

 

5.4广义表

广义表是线性表的推广，列表 lists

广泛地用于人工智能等领域的表处理语言LISP语言，把广义表作为基本的数据结构，就连程序也表示为一系列的广义表。

广义表一般记作

LS = （a1，a2，...，an ）

LS是广义表的名称，n是它的长度。

广义表中的元素可以是单个元素，也可以是广义表，分别称为广义表的原子和子表。

广义表的定义是一个递归的定义。

当广义表非空时，称第一个元素为LS的表头(Head)，其余元素组成的表是LS的表尾(Tail)。

任何非空列表其表头可能是原子，也可能是列表，但其表尾必定为列表。

 

5.5 广义表的存储结构

由于广义表的数据元素可以是原子，也可以是列表，因此难以用顺序存储结构表示，通常采用链式存储结构，每个数据元素可用一个结点表示。

 

需要两种结构的结点：

一种是表结点，用以表示列表；

标志域 + 表头指针域 + 表尾指针域

一种是原子结点，用以表示结点。

标志域 + 值域

两种方式：

 

enum ElemTag {ATOM,LIST};
typedef struct GLNode
{elemTag tag;union{AtomType atom;struct{GLNode *hp, *tp;}ptr;};
}*GList;

 

 

enum ElemTag {ATOM,LIST};
typedef struct GLNode1
{elemTag tag;union{AtomType atom;GLNode1 *hp;};GLNode1 *tp;
}*GList;

 

 

 

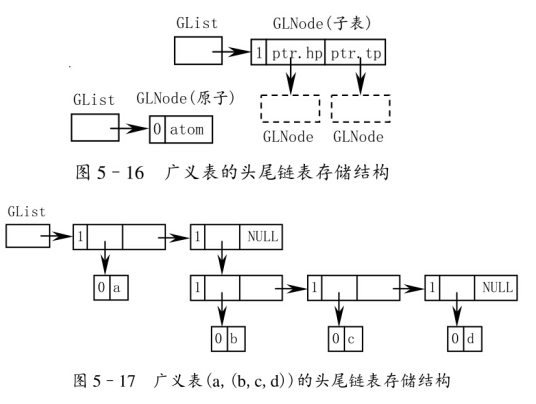
第一种结构：一个列表由表头和表尾组成，表头是一个表，表尾是另一个表。

第一种结构不直观，建议采用第二种结构！

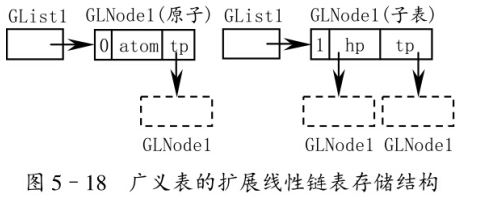
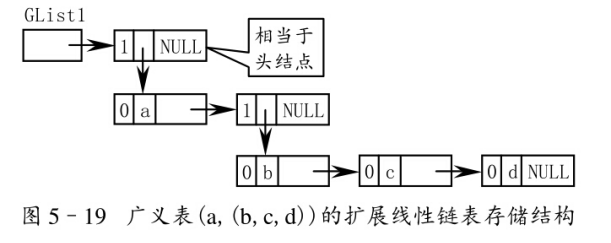
第二种结构：一个列表由表头和表尾组成，表头是原子或列表，表尾是原子或列表。

 

5.7 广义表的递归算法

在对问题进行分解、求解过程中得到的是和原问题性质相同的子问题。

分治法（Divide and Conquer）进行递归算法的设计。

递归定义由基本项和归纳项两部分组成。

基本项：描述一个或几个递归过程的终结状态。

归纳项：描述了如何实现从当前状态到终结状态的变化。

 

在设计递归函数时

（1）首先应书写函数的首部和规格说明，严格定义函数的功能和接口；

（2）对函数中的每一个递归调用都看成是一个简单的操作，只要接口一致，必能实现规格说明中定义的功能，切忌想的太深太远。