利用layui前端框架实现对不同文件夹的多文件上传

问题场景：

普通的input标签实现多文件上传时，只能对同一个文件夹下的多个文件进行上传，如果要同时上传两个或多个文件夹下的文件，是无法实现的。这篇文章就是利用layui中的插件，解决这个问题。

普通多文件上传标签：

前端运用layui

操作步骤：
1、进入layui首页，下载整个组件
2、下载完成后,把名字为layui的文件夹放到你的项目中进行引用
3、引用layui.js和layui.css实现功能
4、可点击可进入layui文件上传实例的官方网址进行参考，来以上三步的前端代码实现

HTML代码块：

<div class="layui-upload"><button type="button" class="layui-btn layui-btn-normal"style="margin-left: 30px"id="testList">选择多文件</button><button type="button" class="layui-btn" id="testListAction"style="display: inline; margin-left: 26px;">开始上传</button><div class="layui-upload-list col-md-12"><table class="layui-table" style="margin: 0 0 0 0"><thead style="display: none"><tr><th>文件名</th><th>大小</th><th>状态</th><th>操作</th></tr></thead><tbody id="demoList"></tbody></table></div>
</div>

JS代码块


<script>layui.use('upload', function () {var $ = layui.jquery, upload = layui.upload;//多文件列表示例var demoListView = $('#demoList'), uploadListIns = upload.render({elem: '#testList', url: '/task_mgm/taskinfo_upload', accept: 'file', multiple: true, auto: false, bindAction: '#testListAction', choose: function (obj) {var files = this.files = obj.pushFile(); //将每次选择的文件追加到文件队列//读取本地文件obj.preview(function (index, file, result) {var tr = $(['<tr id="upload-' + index + '">', '<td>' + file.name + '</td>', '<td>' + (file.size / 1014).toFixed(1) + 'kb</td>', '<td>等待上传</td>', '<td>', '<button class="layui-btn layui-btn-xs demo-reload layui-hide">重传</button>', '<button class="layui-btn layui-btn-xs layui-btn-danger demo-delete">删除</button>', '</td>', '</tr>'].join(''));//单个重传tr.find('.demo-reload').on('click', function () {obj.upload(index, file);});//删除tr.find('.demo-delete').on('click', function () {delete files[index]; //删除对应的文件tr.remove();uploadListIns.config.elem.next()[0].value = ''; //清空 input file 值，以免删除后出现同名文件不可选});demoListView.append(tr);});}, done: function (res, index, upload) {if (res.code == 0) { //上传成功var tr = demoListView.find('tr#upload-' + index), tds = tr.children();tds.eq(2).html('<span style="color: #5FB878;">上传成功</span>');{#tds.eq(3).html(''); //清空操作#}return delete this.files[index]; //删除文件队列已经上传成功的文件}this.error(index, upload);}, error: function (index, upload) {var tr = demoListView.find('tr#upload-' + index), tds = tr.children();tds.eq(2).html('<span style="color: #FF5722;">上传失败</span>');tds.eq(3).find('.demo-reload').removeClass('layui-hide'); //显示重传}});})
</script>

Python后端代码块

UPLOAD_FOLDER = 'static_files/task_mgm/'
# 设置允许上传的文件类型
ALLOWED_EXTENSIONS = set(['txt', 'png', 'jpg', 'xls', 'JPG', 'PNG', 'xlsx', 'gif', 'GIF', 'ppt', 'pptx', 'doc', 'docx', 'csv', 'sql', 'py','rar'])# 用于判断文件后缀
def allowed_file(filename):return '.' in filename and filename.rsplit('.', 1)[1] in ALLOWED_EXTENSIONS@task_mgm.route('/taskinfo_upload',method=['post'])
@login_required
def taskINfo_upload_fun():if request.method == 'POST':# 上传文件的键名是fileif 'file' not in request.files:logging.debugp('No file part')return jsonify({'code': -1, 'filename':'', 'msg':'No file part'})# 获取文件对象file = request.files['file']# 若用户没有选择文件就提交，提示‘No selected file’if file.filename == '':logging.debug('No selected file')return jsonify({'code': -1', 'filename':'', 'msg':'No selected file'})else:try:if file and allowed_file(file.filename):origin_file_name = file.filenamelogging.debug('filename is %s' % origin_file_name)file_dir = os.path.join(os.getcwd(), UPLOAD_FOLDER)if os.path.exists(file_dir):logging.debug('%s path exist' % file_dir)passelse:logging.debug('%s path not exist' % file_dir)os.makedirs(file_dir)file.save(os.path.join(file_dir, filename))return jsonify({'code':0, 'filename':origin_file_name, 'msg': 'save successfully'})else:logging.debug('%s not allowed' % file.filename)return jsonify({'code':-1, 'filename':'', 'msg': 'File not allowed'})except Exception as e:logging.debug(e)return jsonify({'code':-1, 'filename':'', 'msg':'Error occurred'})else:return jsonify({'code':-1, 'filename': '', 'msg':'Method not allowed'})

下面简单展示一下效果图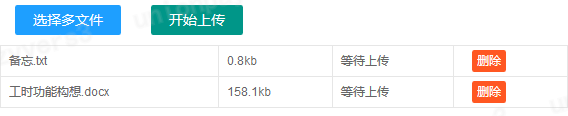：