图(Graph)是由定点的又穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
一、各种图的定义
图按是否有方向分可分为有向图和无向图。有向边用尖括号“<>”表示,无向边用小括号“()”表示。
简单图:无环无重复边。我们以下讨论的都是简单图。
无向完全图:任意两个顶点之间都存在边。
含有n个顶点的无向完全图有n*(n-1)/2条边。
有向完全图:任意两个顶点之间都存在方向互为相反的两条弧。
含有n个顶点的有向完全图有n*(n-1)条边。
网:带权的图。
回路或环:第一个顶点到最后一个顶点相同的路径称为回路或环。
简单路径:序列中顶点不重复出现的路径。
简单回路或简单环:除了第一个顶点和最后一个顶点之外,其余顶点不重复出现的回路。
连通图:任意两个顶点之间互通。
连通分量:无向图中极大连通子图。(要是子图、子图要是连通的、连通子图含有极大顶点数、具有极大定点数的连通子图包含依附于这些顶点的所有边)
二、图的存储方式
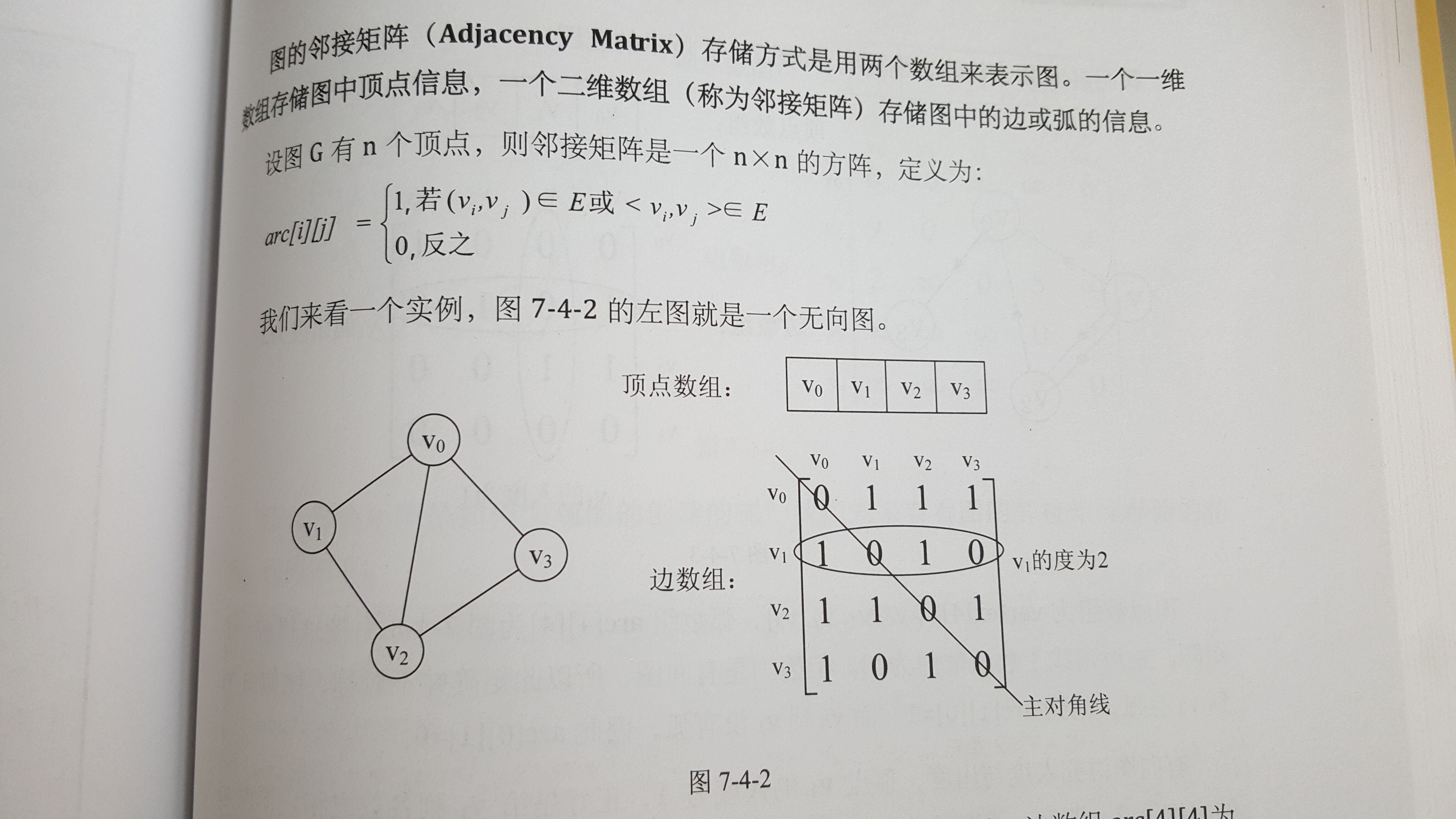
(一)邻接矩阵
邻接矩阵是顶点和边的二维数组,若顶点间存在边,则标作1,否则,标作0。
横着的和是该顶点的度。
(二)邻接表
数组与链表相结合的存储方法。

但在有向图中,一般只关注到出度问题,逆连接表关注到的是入度的问题。
(三)十字链表
把邻接表和逆邻接表结合。
(四)邻接多重表
三、图的遍历
图的遍历指的是从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次。
(一)深度优先遍历
深度优先遍历(Depth_First_Search)DFS,顾名思义,就是从一个顶点出发,往最深里找。
广度优先遍历(Breath_First_Search)BFS,也就是从一个顶点出发,一层层找。
它们的时间复杂度是一样的,只是结点访问的顺序不一样。
四、最小生成树
最小生成树:构造连通网的最小代价生成树。
普里姆算法:从一个点出发,找连通的。
克鲁斯卡尔算法:先找最短的边。
五、最短路径
迪杰斯特拉算法:从一个顶点出发,逐渐找权最小的。
弗洛伊德算法
如果要求所有点到其他点的最短路径,选弗洛伊德算法。
六、关键路径
一个个去掉度为0的顶点。



















