查找（Searching）是根据给定的某个值，在查找表中确定一个其关键字等于给定值的数据元素（或记录）。

一、顺序表查找

顺序查找又叫线性查找，是最基本的查找技术，它的查找过程是：从表中第一个（或最后一个）记录开始，逐个记性记录的关键字和给定值比较，若某个记录的关键字和给定值相等，则查找陈宫，找到所查的记录；如果直到最后一个（或第一个）记录，其关键字和给定值比较都不等时，则表中没有所查的记录，查找不成功。
时间复杂度为O(n)。

二、有序表查找

（一）折半查找
折半查找又称二分查找。它的前提是线性表中的记录必须是关键码有序（通常是从小到大有序），线性表必须采用顺序存储。
折半查找的基本思想是：在有序表中，取中间记录作为比较对象，若给定值与中间记录的关键字相等，则查找成功；若给定值小于中间记录的关键字，则在中间记录的左半区继续查找；若给定值大于中间记录的关键字，则在中间记录的右半区继续查找。不断重复上述过程，直到查找成功，或所有查找区域无记录，查找失败为止。
时间复杂度为O(logn）

（二）插值查找
插值查找的关键是根据要查找的关键字key与查找表中最大最小记录的关键字比较后的查找方法，其核心就在于插值的计算公式（key-a[low]）/(a[high]-a[low])。
从时间复杂度上看，它也是O(logn），但对于表长比较大，而关键字分布又比较均匀的查找表来说，插值查找算法的平均性能比这般查找要好很多。

（三）斐波那契查找

三、线性索引查找

索引是把一个关键字与它对应的记录相关联的过程。一个索引由若干个索引构成，每个索引项至少应包含关键字和其对应的记录在存储器中的位置等信息。
线性索引是将索引项集合组织委员线性结构，称为索引表。 以下重点介绍三种线性索引：稠密索引、分块索引、倒排索引。

（一）稠密索引
稠密索引是指在线性索引中，将数据集中的每个记录对应一个索引项。
稠密索引要应对的可能是成千上万的数据，因此对于稠密索引这个索引表来说，索引项一定是按照关键码有序的排列。

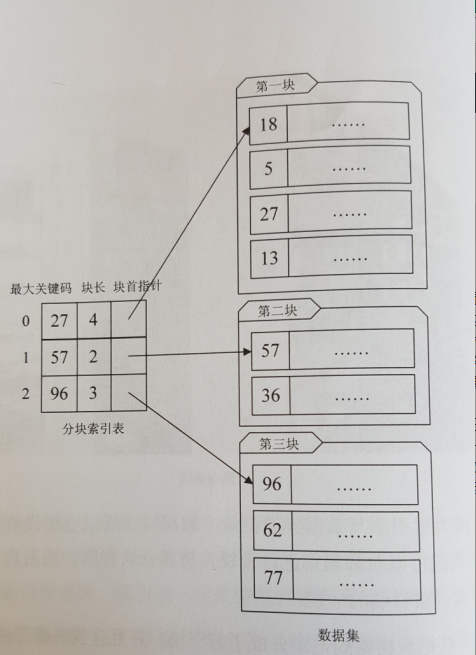
（二）分块索引
例子：图书馆藏书。
分块有序，是把数据集的记录分成了若干块，将每块对应一个索引项，并且这些块需要满足：
（1）块内无序，即每一块内的记录不要求有序。当然，你如果能够让块内有序对查找来说更理想，不过这就要付出大量时间和空间代价，因此通常我们不要求快内有序。
（2）块间有序，例如，要求第二块所有记录的关键字均要大于第一块中所有记录的关键字，第三块所有记录的关键字均要大于第二块的所有记录关键字……因为只有块间有序，才有可能在查找时带来效率。
分块索引的索引项结构分为三个数据项：
（1）最大关键码，存储每一块中的最大关键字；
（2）存储了块中的记录个数，以便循环时用；
（3）用于指向块首数据元素的指针，便于开始对这一块中记录进行遍历。

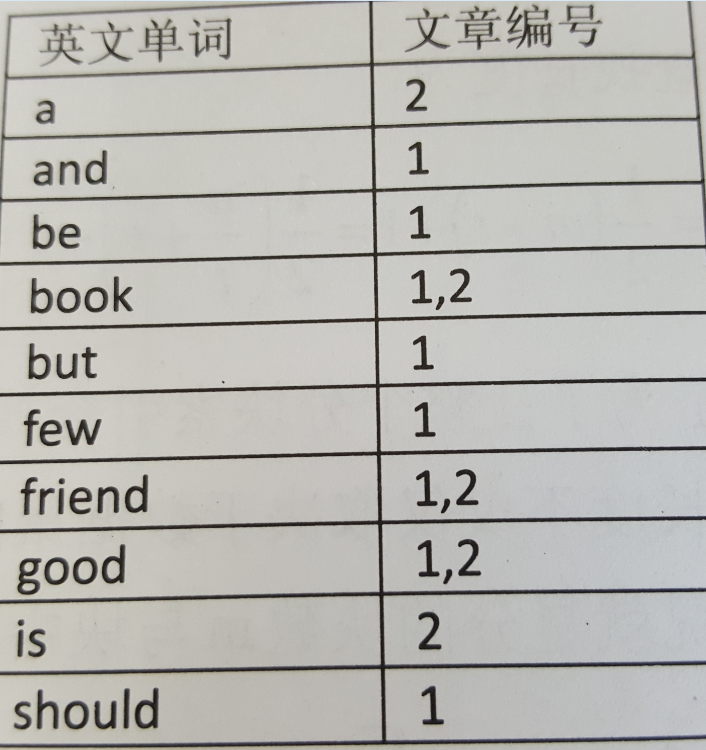
（三）倒排索引
网页搜索一般用的就是倒排索引。
倒排索引的通用结构是：

• 次关键码（如“英文单词”）
• 记录号表（如“文章编号”）

记录号表存储具有相同次关键字的所有记录的记录号（可以是指向记录的指针或者是该记录的主关键字）

四、二叉排序树

二叉排序树又称为二叉查找树。它或者是一棵空树，或者是具有下列性质的二叉树。

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结构的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结构的值；
• 它的左、右子树也分别为二叉排序树。
  按中序遍历它是棵有序树。

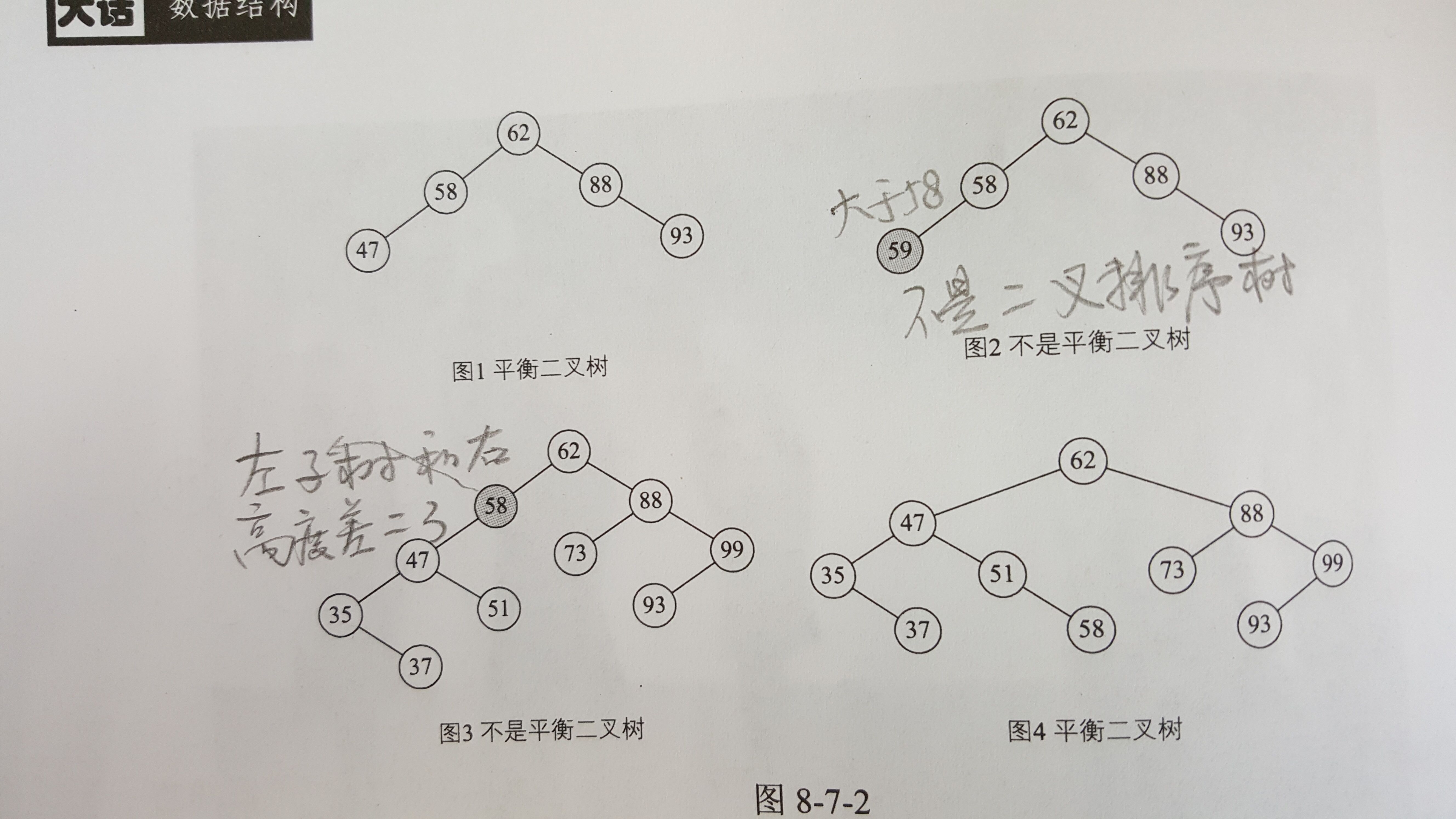
五、平衡二叉树（AVL树）

平衡二叉树，是一种二叉排序树，其中每一个结点的左子树和右子树的高度差至多等于1。

六、多路查找树（B树）

多路查找树，其每一个结点的孩子书可以多于两个，且每一个结点处可以存储多个元素。

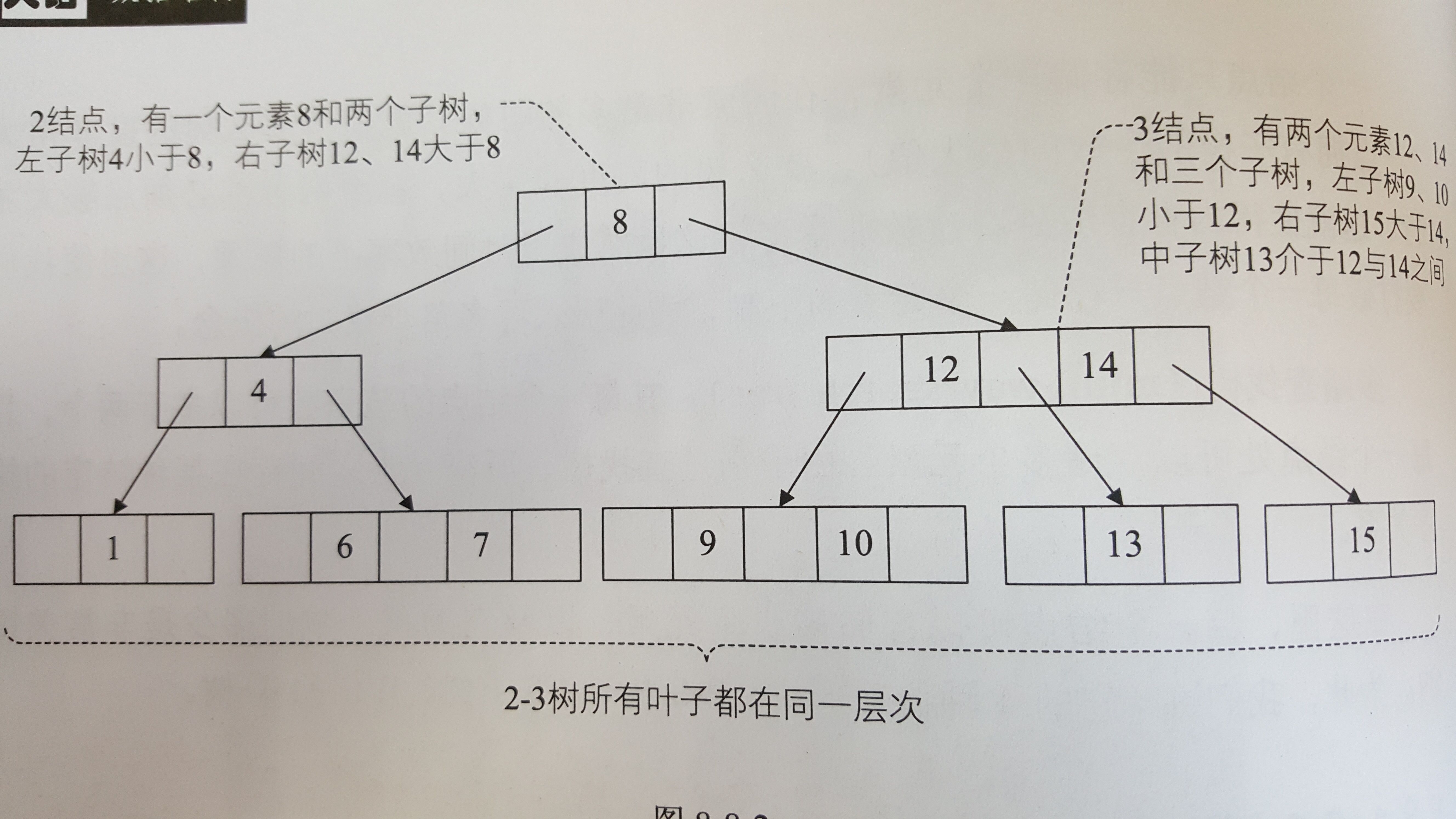
（一）2-3树
2-3树是一棵多路查找树：其中的每一个结点都具有两个孩子（称为2结点）或三个孩子（称为3结点）。
一个2结点包含一个元素和两个孩子（或没有孩子）。
一个3结点包含一小一大两个元素和三个孩子（或没有孩子）。

（二）2-3-4树
2-3-4树是2-3树的扩展，包括了4个结点的使用。一个结点包含小中大三个元素和四个孩子（或没有孩子）。

（三）B树
B树是一种平衡的多路查找树，2-3树和2-3-4树都是B树的特例。结点最大的孩子数目称为B树的阶，因此，2-3树是3阶的B树，2-3-4树是4阶的B树。

（四）B+树

七、散列表查找（哈希表）概述

散列技术是在记录的存储位置和它的关键字之间建立一个确定的对应关系f，使得每个关键字key对应一个存储位置f（key）。查找时，根据这个确定的对应关系找到给定值key的映射f（key），若查找集合中存在这个记录，则必定在f（key）的位置上。
我们把上述的对应关系f称为散列函数，又称为哈希函数。采用散列技术将记录存储在一块连续的存储空间中，这块连续存储空间称为散列表后哈希表。