HDU - 4578Transformation——线段树+区间加法修改+区间乘法修改+区间置数+区间和查询+区间平方和查询+区间立方和查询

【题目描述】
HDU - 4578Transformation
Problem Description
Yuanfang is puzzled with the question below:
There are n integers, a1, a2, …, an. The initial values of them are 0. There are four kinds of operations.
Operation 1: Add c to each number between ax and ay inclusive. In other words, do transformation ak<—ak+c, k = x,x+1,…,y.
Operation 2: Multiply c to each number between ax and ay inclusive. In other words, do transformation ak<—ak×c, k = x,x+1,…,y.
Operation 3: Change the numbers between ax and ay to c, inclusive. In other words, do transformation ak<—c, k = x,x+1,…,y.
Operation 4: Get the sum of p power among the numbers between ax and ay inclusive. In other words, get the result of axp+ax+1p+…+ay p.
Yuanfang has no idea of how to do it. So he wants to ask you to help him.

Input
There are no more than 10 test cases.
For each case, the first line contains two numbers n and m, meaning that there are n integers and m operations. 1 <= n, m <= 100,000.
Each the following m lines contains an operation. Operation 1 to 3 is in this format: “1 x y c” or “2 x y c” or “3 x y c”. Operation 4 is in this format: “4 x y p”. (1 <= x <= y <= n, 1 <= c <= 10,000, 1 <= p <= 3)
The input ends with 0 0.

Output
For each operation 4, output a single integer in one line representing the result. The answer may be quite large. You just need to calculate the remainder of the answer when divided by 10007.

Sample Input

5 5
3 3 5 7
1 2 4 4
4 1 5 2
2 2 5 8
4 3 5 3
0 0

Sample Output

307
7489
【题目分析】
这道题真的是老妖怪级别的了，此处省略吐槽两千字
题目的意思很明确，就是给你一个全为0 的数组，让你实现区间加法修改+区间乘法修改+区间置数+区间和查询+区间平方和查询+区间立方和查询功能。
根据需求，每个区间有三个需要维护的数据——区间和，区间平方和，区间立方和，有三种修改操作，因此需要三种标记，分别用来标记区间加法、区间乘法、区间置数
难点在于对于三种数据的快速维护和标记之间的关系

标记之间的关系（关键）
我们为了实现区间修改就需要引入lazy标记（没有掌握这个的同学请出门左拐，详见线段树入门），但是当存在多种标记的时候处理标记的顺序就很重要，因为这反应了修改操作的效用关系以及时间关系。
上面三种操作里面最厉害的显然是区间置数，一个区间置数后之前什么加法乘法统统作废。然后是区间乘法，因为区间乘法，因为对同一个区间，后来的乘法标记会对之前的加法标记产生影响，但是后来的加法标记对乘法标记却没有什么影响（先算乘法再算加法嘛）
因此在处理区间置数的时候可以直接对区间加法置零，对区间乘法的标记置一
在处理区间乘法的时候如果发现下面的区间还要进行区间加法就要修改区间加法的标记（给标记也乘上同一个数）
在处理区间加法的时候对其他标记没有影响
同样的，在下传标记的时候同样要面对这样的问题
这样，后面的操作对前面操作的影响就能传递下去
三种数据的快速维护
区间置数后三种数据直接计算
区间乘法后立方和乘上乘数的立方，平方和乘上乘数的平方，区间和乘上乘数，需要注意取模（时刻取模，时刻提防爆数据）
最麻烦的是区间加法
对于区间和，应该加上区间长度乘上加数
对于平方和，见下图

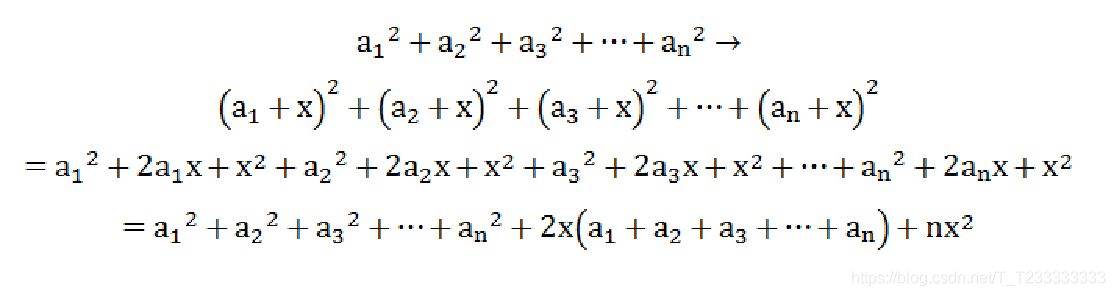
立方和同理
【AC代码】（可写死我了）

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<string>
#include<climits>
#include<queue>
#include<vector>using namespace std;
typedef long long ll;const int MAXN=100005;
const ll MOD=10007;struct node
{ll a,aa,aaa;
}tree[MAXN<<2];
ll set[MAXN<<2],add[MAXN<<2],multiply[MAXN<<2];
int n,m;
ll t;void pushdown(int k,int l,int r)
{int mid=(l+r)>>1; if(set[k]>0){tree[k<<1].a=set[k]%MOD*(mid-l+1)%MOD; tree[k<<1|1].a=set[k]%MOD*(r-mid)%MOD;tree[k<<1].aa=set[k]%MOD*set[k]%MOD*(mid-l+1)%MOD; tree[k<<1|1].aa=set[k]%MOD*set[k]%MOD*(r-mid)%MOD;tree[k<<1].aaa=set[k]%MOD*set[k]%MOD*set[k]%MOD*(mid-l+1)%MOD; tree[k<<1|1].aaa=set[k]%MOD*set[k]%MOD*set[k]%MOD*(r-mid)%MOD;set[k<<1]=set[k<<1|1]=set[k];	add[k<<1]=add[k<<1|1]=0;	//直接取消标记multiply[k<<1]=multiply[k<<1|1]=1;	//直接取消标记set[k]=0;}if(multiply[k]!=1){tree[k<<1].a=tree[k<<1].a*multiply[k]%MOD;tree[k<<1|1].a=tree[k<<1|1].a*multiply[k]%MOD;tree[k<<1].aa=tree[k<<1].aa*multiply[k]%MOD*multiply[k]%MOD;tree[k<<1|1].aa=tree[k<<1|1].aa*multiply[k]%MOD*multiply[k]%MOD;tree[k<<1].aaa=tree[k<<1].aaa*multiply[k]%MOD*multiply[k]%MOD*multiply[k]%MOD;tree[k<<1|1].aaa=tree[k<<1|1].aaa*multiply[k]%MOD*multiply[k]%MOD*multiply[k]%MOD;multiply[k<<1]=multiply[k<<1]*multiply[k]%MOD;multiply[k<<1|1]=multiply[k<<1|1]*multiply[k]%MOD;if(add[k<<1]) add[k<<1]=add[k<<1]*multiply[k]%MOD;	//注意对加法标记的影响if(add[k<<1|1]) add[k<<1|1]=add[k<<1|1]*multiply[k]%MOD;-multiply[k]=1;}if(add[k]>0){tree[k<<1].aaa=(((tree[k<<1].aaa+3*add[k]%MOD*tree[k<<1].aa%MOD)%MOD+3*add[k]%MOD*add[k]%MOD*tree[k<<1].a%MOD)%MOD+(mid-l+1)*add[k]%MOD*add[k]%MOD*add[k]%MOD)%MOD; //顺序很重要，应该先立方后平方再区间和（因为会用到原始数据）tree[k<<1|1].aaa=(((tree[k<<1|1].aaa+3*add[k]%MOD*tree[k<<1|1].aa%MOD)%MOD+3*add[k]%MOD*add[k]%MOD*tree[k<<1|1].a%MOD)%MOD+(r-mid)*add[k]%MOD*add[k]%MOD*add[k]%MOD)%MOD; tree[k<<1].aa=((tree[k<<1].aa+add[k]*add[k]%MOD*(mid-l+1)%MOD)%MOD+2*add[k]%MOD*tree[k<<1].a%MOD)%MOD;tree[k<<1|1].aa=((tree[k<<1|1].aa+add[k]*add[k]%MOD*(r-mid)%MOD)%MOD+2*add[k]%MOD*tree[k<<1|1].a%MOD)%MOD;tree[k<<1].a=(tree[k<<1].a+add[k]*(mid-l+1)%MOD)%MOD;tree[k<<1|1].a=(tree[k<<1|1].a+add[k]*(r-mid)%MOD)%MOD;add[k<<1]=(add[k<<1]+add[k])%MOD;add[k<<1|1]=(add[k<<1|1]+add[k])%MOD;//时刻注意取模add[k]=0;}
}void update(int k)
{tree[k].a=(tree[k<<1].a+tree[k<<1|1].a)%MOD;tree[k].aa=(tree[k<<1].aa+tree[k<<1|1].aa)%MOD;tree[k].aaa=(tree[k<<1].aaa+tree[k<<1|1].aaa)%MOD;
}void interval_add(int k,int l,int r,int x,int y,ll z)
{if(l>=x && r<=y){tree[k].aaa=(((tree[k].aaa+3*z%MOD*tree[k].aa%MOD)%MOD+3*z%MOD*z%MOD*tree[k].a)%MOD+(r-l+1)*z%MOD*z%MOD*z%MOD)%MOD;tree[k].aa=((tree[k].aa+2*z%MOD*tree[k].a%MOD)%MOD+(r-l+1)*z%MOD*z%MOD)%MOD;tree[k].a=(tree[k].a+z*(r-l+1)%MOD)%MOD;add[k]=(add[k]+z)%MOD;return;}int mid=(l+r)>>1;pushdown(k,l,r);if(x<=mid) interval_add(k<<1,l,mid,x,y,z);if(y>mid) interval_add(k<<1|1,mid+1,r,x,y,z);update(k); 
}void interval_multiply(int k,int l,int r,int x,int y,ll z)
{if(l>=x && r<=y){multiply[k]=(multiply[k]*z)%MOD;if(add[k]>0){add[k]=(add[k]*z)%MOD;}tree[k].a=tree[k].a*z%MOD;tree[k].aa=tree[k].aa*z%MOD*z%MOD;tree[k].aaa=tree[k].aaa*z%MOD*z%MOD*z%MOD;return;}int mid=(l+r)>>1;pushdown(k,l,r);if(x<=mid) interval_multiply(k<<1,l,mid,x,y,z);if(y>mid) interval_multiply(k<<1|1,mid+1,r,x,y,z);update(k); 
}void interval_set(int k,int l,int r,int x,int y,ll z)
{if(l>=x && r<=y){tree[k].a=z*(r-l+1)%MOD;tree[k].aa=z*z%MOD*(r-l+1)%MOD;tree[k].aaa=z*z%MOD*z%MOD*(r-l+1)%MOD;add[k]=0;multiply[k]=1;set[k]=z;return;}int mid=(l+r)>>1;pushdown(k,l,r);if(x<=mid) interval_set(k<<1,l,mid,x,y,z);if(y>mid) interval_set(k<<1|1,mid+1,r,x,y,z);update(k); 
}ll query(int k,int l,int r,int x,int y,int z)
{if(l>=x && r<=y){if(z==1)return tree[k].a%MOD;if(z==2)return tree[k].aa%MOD;if(z==3)return tree[k].aaa%MOD;}int mid=(l+r)>>1;ll ans=0;pushdown(k,l,r);if(x<=mid) ans=(ans+query(k<<1,l,mid,x,y,z))%MOD;if(y>mid) ans=(ans+query(k<<1|1,mid+1,r,x,y,z))%MOD;return ans;
}void search_point(int k,int l,int r,int x)
{if(l==r && l==x){t=tree[k].a;return;}pushdown(k,l,r);int mid=(l+r)>>1;if(x<=mid) search_point(k<<1,l,mid,x);else search_point(k<<1|1,mid+1,r,x);
}void test()
{for(int i=1;i<=n;i++){search_point(1,1,n,i);printf("%lld ",t);}printf("\n");
}int main()
{ll cmd,u,v,w;while(~scanf("%d%d",&n,&m) && (n||m)){memset(tree,0,sizeof(tree));memset(set,0,sizeof(set));memset(add,0,sizeof(add));for(int i=0,j=n<<2;i<=j;i++) multiply[i]=1;for(int i=0;i<m;i++){scanf("%lld%lld%lld%lld",&cmd,&u,&v,&w);if(cmd==1){interval_add(1,1,n,u,v,w%MOD);}else if(cmd==2){interval_multiply(1,1,n,u,v,w%MOD);}else if(cmd==3){interval_set(1,1,n,u,v,w%MOD);}else if(cmd==4){//test();printf("%lld\n",query(1,1,n,u,v,w));}}}return 0;
}