树链剖分入门讲解

“在一棵树上进行路径的修改、求极值、求和”乍一看只要线段树就能轻松解决，实际上，仅凭线段树是不能搞定它的。我们需要用到一种貌似高级的复杂算法——树链剖分。

树链，就是树上的路径。剖分，就是把路径分类为重链和轻链。
记siz[v]表示以v为根的子树的节点数，dep[v]表示v的深度(根深度为1)，top[v]表示v所在的重链的顶端节点，fa[v]表示v的父亲，son[v]表示与v在同一重链上的v的儿子节点（姑且称为重儿子），w[v]表示v与其父亲节点的连边（姑且称为v的父边）在线段树中的位置。只要把这些东西求出来，就能用logn的时间完成原问题中的操作。

重儿子：siz[u]为v的子节点中siz值最大的，那么u就是v的重儿子。
轻儿子：v的其它子节点。
重边：点v与其重儿子的连边。
轻边：点v与其轻儿子的连边。
重链：由重边连成的路径。
轻链：轻边。

剖分后的树有如下性质：
性质1：如果(v,u)为轻边，则siz[u] * 2 < siz[v]；
性质2：从根到某一点的路径上轻链、重链的个数都不大于logn。

算法实现：
我们可以用两个dfs来求出fa、dep、siz、son、top、w。
dfs_1：把fa、dep、siz、son求出来，比较简单，略过。
dfs_2：⒈对于v，当son[v]存在（即v不是叶子节点）时，显然有top[son[v]] = top[v]。线段树中，v的重边应当在v的父边的后面，记w[son[v]] = totw+1，totw表示最后加入的一条边在线段树中的位置。此时，为了使一条重链各边在线段树中连续分布，应当进行dfs_2(son[v])；
⒉对于v的各个轻儿子u，显然有top[u] = u，并且w[u] = totw+1，进行dfs_2过程。
这就求出了top和w。
将树中各边的权值在线段树中更新，建链和建线段树的过程就完成了。

修改操作：例如将u到v的路径上每条边的权值都加上某值x。
一般人需要先求LCA，然后慢慢修改u、v到公共祖先的边。而高手就不需要了。
记f1 = top[u]，f2 = top[v]。
当f1 <> f2时：不妨设dep[f1] >= dep[f2]，那么就更新u到f1的父边的权值(logn)，并使u = fa[f1]。
当f1 = f2时：u与v在同一条重链上，若u与v不是同一点，就更新u到v路径上的边的权值(logn)，否则修改完成；
重复上述过程，直到修改完成。

求和、求极值操作：类似修改操作，但是不更新边权，而是对其求和、求极值。
就这样，原问题就解决了。鉴于鄙人语言表达能力有限，咱画图来看看：
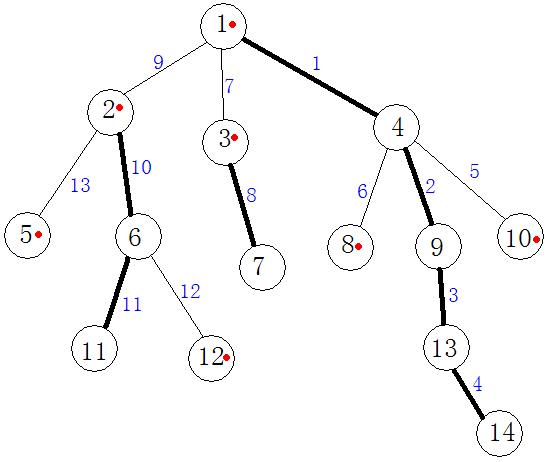
树链剖分分析

如上图所示，较粗的为重边，较细的为轻边。节点编号旁边有个红色点的表明该节点是其所在链的顶端节点。边旁的蓝色数字表示该边在线段树中的位置。图中1-4-9-13-14为一条重链。

当要修改11到10的路径时。
第一次迭代：u = 11，v = 10，f1 = 2，f2 = 10。此时dep[f1] < dep[f2]，因此修改线段树中的5号点，v = 4, f2 = 1；
第二次迭代：dep[f1] > dep[f2]，修改线段树中10–11号点。u = 2，f1 = 2；
第三次迭代：dep[f1] > dep[f2]，修改线段树中9号点。u = 1，f1 = 1；
第四次迭代：f1 = f2且u = v，修改结束。

**数据规模大时，递归可能会爆栈，而非递归dfs会很麻烦，所以可将两个dfs改为宽搜+循环。即先宽搜求出fa、dep，然后逆序循环求出siz、son，再顺序循环求出top和w。
题目：spoj375、USACO December Contest Gold Divison, “grassplant”。
**spoj375据说不“缩行”情况下最短的程序是140+行，我的是128行。

#include <cstdio>
#include <algorithm>
#include <iostream>
#include <string.h>
using namespace std;
const int maxn = 10010;
struct Tedge
{ int b, next; } e[maxn * 2];
int tree[maxn];
int zzz, n, z, edge, root, a, b, c;
int d[maxn][3];
int first[maxn], dep[maxn], w[maxn], fa[maxn], top[maxn], son[maxn], siz[maxn];
char ch[10];void insert(int a, int b, int c)
{e[++edge].b = b;e[edge].next = first[a];first[a] = edge;
}void dfs(int v)
{siz[v] = 1; son[v] = 0;for (int i = first[v]; i > 0; i = e[i].next)if (e[i].b != fa[v]){fa[e[i].b] = v;dep[e[i].b] = dep[v]+1;dfs(e[i].b);if (siz[e[i].b] > siz[son[v]]) son[v] = e[i].b;siz[v] += siz[e[i].b];}
}void build_tree(int v, int tp)
{w[v] = ++ z; top[v] = tp;if (son[v] != 0) build_tree(son[v], top[v]);for (int i = first[v]; i > 0; i = e[i].next)if (e[i].b != son[v] && e[i].b != fa[v])build_tree(e[i].b, e[i].b);
}void update(int root, int lo, int hi, int loc, int x)
{if (loc > hi || lo > loc) return;if (lo == hi){ tree[root] = x; return; }int mid = (lo + hi) / 2, ls = root * 2, rs = ls + 1;update(ls, lo, mid, loc, x);update(rs, mid+1, hi, loc, x);tree[root] = max(tree[ls], tree[rs]);
}int maxi(int root, int lo, int hi, int l, int r)
{if (l > hi || r < lo) return 0;if (l <= lo && hi <= r) return tree[root];int mid = (lo + hi) / 2, ls = root * 2, rs = ls + 1;return max(maxi(ls, lo, mid, l, r), maxi(rs, mid+1, hi, l, r));
}inline int find(int va, int vb)
{int f1 = top[va], f2 = top[vb], tmp = 0;while (f1 != f2){if (dep[f1] < dep[f2]){ swap(f1, f2); swap(va, vb); }tmp = max(tmp, maxi(1, 1, z, w[f1], w[va]));va = fa[f1]; f1 = top[va];}if (va == vb) return tmp;if (dep[va] > dep[vb]) swap(va, vb);return max(tmp, maxi(1, 1, z, w[son[va]], w[vb]));  //
}void init()
{scanf("%d", &n);root = (n + 1) / 2;fa[root] = z = dep[root] = edge = 0;memset(siz, 0, sizeof(siz));memset(first, 0, sizeof(first));memset(tree, 0, sizeof(tree));for (int i = 1; i < n; i++){scanf("%d%d%d", &a, &b, &c);d[i][0] = a; d[i][1] = b; d[i][2] = c;insert(a, b, c);insert(b, a, c);}dfs(root);build_tree(root, root);    //for (int i = 1; i < n; i++){if (dep[d[i][0]] > dep[d[i][1]]) swap(d[i][0], d[i][1]);update(1, 1, z, w[d[i][1]], d[i][2]);}
}inline void read()
{ch[0] = ' ';while (ch[0] < 'C' || ch[0] > 'Q') scanf("%s", &ch);
}void work()
{for (read(); ch[0] != 'D'; read()){scanf("%d%d", &a, &b);if (ch[0] == 'Q') printf("%d\n", find(a, b));else update(1, 1, z, w[d[a][1]], b);}
}int main()
{for (scanf("%d", &zzz); zzz > 0; zzz--){init();work();}return 0;
}