❓剑指 Offer 11. 旋转数组的最小数字
难度:简单
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
给你一个可能存在 重复 元素值的数组 numbers ,它原来是一个升序排列的数组,并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转,该数组的最小值为 1。
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
示例 1:
输入:numbers = [3,4,5,1,2]
输出:1
示例 2:
输入:numbers = [2,2,2,0,1]
输出:0
提示:
n == numbers.length1 <= n <= 5000-5000 <= numbers[i] <= 5000numbers原来是一个升序排序的数组,并进行了1至n次旋转
注意:本题与 154. 寻找旋转排序数组中的最小值 II 相同。
💡思路:二分查找
将旋转数组对半分可以得到一个包含最小元素的新旋转数组,以及一个非递减排序的数组。新的旋转数组的长度是原数组的一半,从而将问题规模减少了一半,这种折半性质的算法的时间复杂度为 O ( l o g 2 N ) O(log2N) O(log2N)。
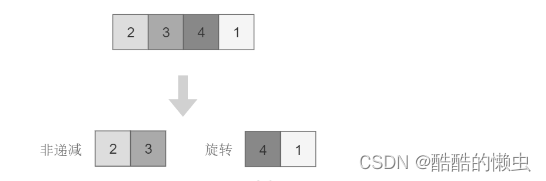
此时问题的关键在于确定对半分得到的两个数组哪一个是旋转数组,哪一个是非递减数组。我们很容易知道非递减数组的第一个元素一定小于等于最后一个元素。
通过修改二分查找算法进行求解(left、mid、right 分别代表包含最小元素的新旋转数组 左、中、右):
- 当
numbers[mid] > numbers[right]时,[left,mid]区间内的数组是非递减数组,[mid + 1, right]区间内的数组为新的旋转数组,此时,left = mid + 1; - 当
numbers[mid] < numbers[right]时,[mid,right]区间内的数组是非递减数组,[left, mid]区间内的数组为新的旋转数组,此时,right = mid; - 当
numbers[mid] = numbers[right]时, 无法判断哪一个是旋转数组,哪一个是非递减数组,此时right- -,直到能判断。
🍁代码:(C++、Java)
C++
class Solution {
public:int minArray(vector<int>& numbers) {int left = 0;int right = numbers.size() - 1;if(right == 0) return numbers[0];while(left < right){int mid = left + (right - left) / 2;if(numbers[mid] > numbers[right]){left = mid + 1;}else if(numbers[mid] < numbers[right]){right = mid;}else{right--;}}return numbers[left];}
};
Java
class Solution {public int minArray(int[] numbers) {int left = 0;int right = numbers.length - 1;if(right == 0) return numbers[0];while(left < right){int mid = left + (right - left) / 2;if(numbers[mid] > numbers[right]){left = mid + 1;}else if(numbers[mid] < numbers[right]){right = mid;}else{right--;}}return numbers[left];}
}
🚀 运行结果:
🕔 复杂度分析:
- 时间复杂度: O ( l o g n ) O(logn) O(logn),平均时间复杂度为 O ( l o g n ) O(logn) O(logn),其中
n是数组numbers的长度。如果数组是随机生成的,那么数组中包含相同元素的概率很低,在二分查找的过程中,大部分情况都会忽略一半的区间。而在最坏情况下,如果数组中的元素完全相同,那么while循环就需要执行n次,每次忽略区间的右端点,时间复杂度为O(n)。 - 空间复杂度: O ( 1 ) O(1) O(1)。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我LeetCode主页 / CSDN—力扣专栏,每日更新!




——CentOS7定时任务)


)
)










