
二项分布是概率统计中非常基础、非常实用的一种分布,可以说它在我们的生活中无所不在。它说明了这样一种现象:在给定的试验次数中,某一结果会发生多少次。
比如:
这个月有多少天会刮北风?
今年有多少天会下雨?
经过一个路口100次,有多少次会是绿灯?
一年之中会有多少次出门就见狗?
伯努利分布伯努利分布是二项分布的基础,它只有两种状态,比如抛硬币的时候,结果只有正面和反面两种情况,且两种情况的概率之和为1。也就是说,当我们给定正面朝上的概率的时候,这个分布的一切就都确定了。
我们以0和1来标识这两种可能的结果,那么其概率函数为:
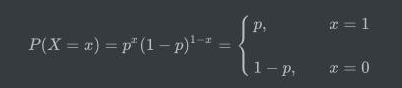
那么其期望值为:
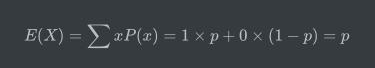
其方差为:
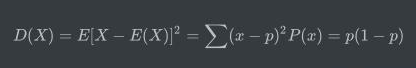 排列组合
排列组合1. 排列
从n个对象中有序地挑选出r个对象,我们称之为排列,我们用以下公式统计其可能产生的排列数:
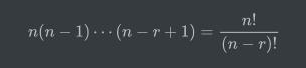
2. 组合
考虑另一种情况,仍然是从n个对象中抽取r个对象,但是这次我们不考虑其顺序,这种过程我们称之为组合。我们用以下公式统计其可能产生的组合数:
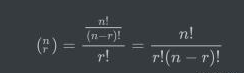
可以看出,这是n选r的排列数除以r的排列数。上述公式又被称作二项系数,通常用“n选r”表示。
3. Python计算
那么接下来我们用Python来写一个函数,用来计算不同参数下的排列与组合的数量。在排列组合的计算中,我们可能会输入两个参数:总样本量n、需要抽取的样本数k。
那么我们就定义如下函数:
from functools import reducedef PC(n, k): """ 计算并返回排列组合数 """ # 非法输入返回空 if n <= 0 or k < 0 or n < k: print('Wrong Input!') return None # k为0时,排列组合的情况恒为1 if k == 0: return 1, 1 # 生成正序及倒序的序列 series_asc = list(range(1, n+1)) series_desc = sorted(series_asc, reverse=True) # 排列 permutation = reduce(lambda x, y: x*y, series_desc[:k]) # 组合 perm2 = reduce(lambda x, y: x*y, series_asc[:k]) combination = int(permutation / perm2) return permutation, combination随手测试几个:
for n in range(1, 5): for k in range(1, 3): print('-'*10) print(n, k) print(PC(n, k))结果是正确的:
----------1 1(1, 1)----------1 2Wrong Input!None----------2 1(2, 2)----------2 2(2, 1)----------3 1(3, 3)----------3 2(6, 3)----------4 1(4, 4)----------4 2(12, 6)回顾伯努利分布的情况:一次实验只有可能有两种结果,分别用0和1来表示,其中结果1发生的概率为p。那么在n次独立实验中,不考虑顺序的情况下,结果1出现k次的概率是多少?
首先,因为n次实验相互独立,所以根据乘法定律,任何一种结果1出现k次的场景发生的概率均为:
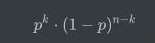
然后,我们需要考虑结果为1的次数刚好为k的情况有多少种。很明显,这就是一个伯努利试验的组合问题,n次实验中有k次结果为1的情况共有“n选k”种,两者相乘就是该事件发生的概率。
因此:
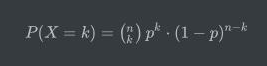 Python计算
Python计算那么我们来用Python实现一个计算二项分布概率的小工具,在这里,我们的输入参数包含总试验次数n、正样本发生的次数k以及正样本发生的概率p:
def binominal_prob(n, k, p): """ 计算并返回二项分布中某结果发生的概率 """ # 任一k次成功的序列出现的概率 p_base = p ** k * (1-p) ** (n-k) # n次试验中k次成功的组合数 # 直接用上边我们编写的排列组合函数来求解 combination = PC(n, k)[1] p_result = p_base * combination return p_result那么接下来,我们利用我们刚刚写好的小工具,来看一下在10次试验中,不同的概率对应的二项分布是什么样的。
probs = [binominal_prob(10, i, 0.5) for i in range(11)]我们将结果画出来看看:
%matplotlib inlineimport numpy as npimport matplotlib.pyplot as pltimport seaborn as snssns.set()probs = [round(i/10,1) for i in range(1, 10)]n = 20plt.figure(figsize=(16, 6))for p in probs: dist_probs = [binominal_prob(n, i, p) for i in range(n+1)] plt.plot(range(n+1), dist_probs, label='p={0}'.format(p))plt.legend()plt.title('Binominal Distributions of Different P value')plt.savefig('binominal.jpg')plt.show()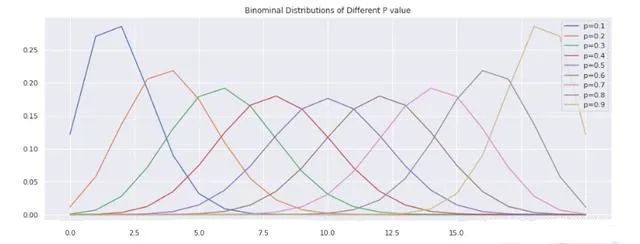
或者我们使用交互式的绘图库plotly来尝试同样的事情:
import plotly.graph_objects as goprobs = [round(i/10,1) for i in range(1, 10)]n = 20fig = go.Figure()for p in probs: dist_probs = [binominal_prob(n, i, p) for i in range(n+1)] fig.add_trace(go.Scatter( x=list(range(n+1)), y=dist_probs, name='p={0}'.format(p) ))fig.show()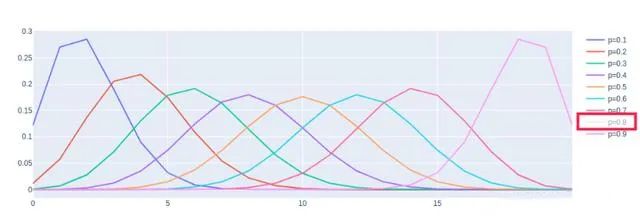
可以看到,plotly实现的效果更加靓丽,且额外支持了动态交互,在这里我就选择把p=0.8这条线隐藏了起来。
一个利用极大似然估计求二项分布概率参数的例子我们现在想象一种情况,有一枚分布不太均匀的硬币,每次抛向空中后,落地为正面的概率为p,任意两次实验之间相互独立。现在我们做了4次实验,其中有三次正面朝上,那么请问p的值为多少?
我们之前曾经提到过极大似然估计,在这里我们用同样的思路去估计p的取值。极大似然估计的思想就是寻找一个参数,使得当前结果发生的概率最大,那么我们先定义出来当前结果发生的概率公式:
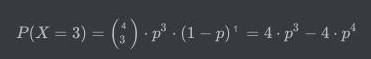
对其求导并使导数为0,有:
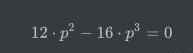
可得,当p=0.75时,P(X=3)=0.422达到最大(另一个解p=0显然不可能,因为硬币朝上已经发生了,并不是“不可能事件”;另外考虑不同区间导数的取值也可以得到答案)。
- END -
文源网络,仅供学习之用,如有侵权,联系删除。
往期精彩
◆ 50款开源工具你都用过吗?
◆ python+C、C++混合编程的应用
◆ python网络爬虫的基本原理详解
◆ Python自动操控excel,一小时解决你一天的工作
◆ 如何用Python增强Excel,减少处理复杂数据的痛苦?



)









:用户持有凭证)



查询)


