• 压缩矩阵：指为多个值相同的元素只分配一个存储空间，对零元素不分配存储空间
• 特殊矩阵：指具有许多相同矩阵元素或零元素，并且这些相同矩阵元素或零元素的分配有一定规律性

1、对称矩阵

对称矩阵：矩阵每个元素都有a_ij=a_ji

压缩方法：将对称矩阵存放到一维数组B[n(n+1)/2]中，第一行先存，依次向下，只存放主对角线和下三角线的元素

元素a_ij在数组B中的下标k=1+2+…+（i-1）+j-1 （这里的i,j都是从1开始的）

2、三角矩阵

三角矩阵：上三角或者下三角都是同一常量

压缩方法：将三角矩阵压缩到一维数组B[n(n+1)/2+1]中，按行优先，数组B最后一个空间存放常量C

元素a_ij在数组B中的下标k （ij都是从1开始）
下三角矩阵：

上三角矩阵：

3、三对角矩阵

三对角矩阵：只有以主对角线为中心的3条对角线为不全为0，其他的都是0

压缩方式：将3条对角线上的元素按行优先存放一维数组B中

元素a_ij在数组B中的下标k （ij都是从1开始）

知道k，如何求i，j？

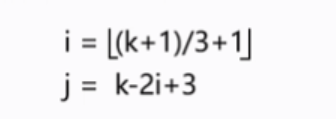
4、稀疏矩阵

稀疏矩阵：矩阵里0元素非常多

压缩方法：仅存储非零元素，存储非零元素的行值、列值、非零元素值，按行优先

i、j从0开始

缺点：稀疏矩阵压缩存储后便失去了随机存取特性（前面的k还可以根据i、j来求)