b tree和b+tree_B TREE实施

b tree和b+tree

B TREE及其操作简介 (Introduction to B TREE and its operations)

A B tree is designed to store sorted data and allows search, insertion and deletion operation to be performed in logarithmic time. As In multiway search tree, there are so many nodes which have left subtree but no right subtree. Similarly, they have right subtree but no left subtree. As is known, access time in the tree is totally dependent on the level of the tree. So our aim is to minimize the access time which can be through balance tree only.

B树设计用于存储排序的数据，并允许在对数时间内执行搜索，插入和删除操作。就像在多路搜索树中一样，有许多节点具有左子树但没有右子树。同样，它们具有右子树，但没有左子树。众所周知，树中的访问时间完全取决于树的级别。因此，我们的目标是最大程度地减少只能通过平衡树访问的时间。

For balancing the tree each node should contain n/2 keys. So the B tree of order n can be defined as:

为了平衡树，每个节点应包含n / 2个键。因此，n阶的B树可以定义为：

All leaf nodes should be at same level.
所有叶节点应处于同一级别。
All leaf nodes can contain maximum n-1 keys.
所有叶节点最多可以包含n-1个密钥。
The root has at least two children.
根至少有两个孩子。
The maximum number of children should be n and each node can contain k keys. Where, k<=n-1.
子代的最大数量应为n，每个节点可以包含k个键。其中，k <= n-1。
Each node has at least n/2 and maximum n nonempty children.
每个节点至少具有n / 2个，最多n个非空子代。
Keys in the non-leaf node will divide the left and right sub-tree where the value of left subtree keys will be less and value of right subtree keys will be more than that particular key.
非叶节点中的键将划分左右子树，其中左子树键的值将小于该左子树，而右子树键的值将大于该特定键。

Let us take a B-tree of order 5,

让我们以5阶的B树为例

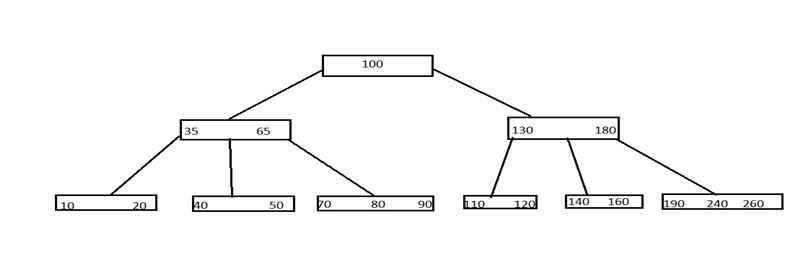
Here, we can see all leaf nodes are at same level. All non-leaf nodes have no empty sub-tree and they have keys 1 less than the number of their children.

在这里，我们可以看到所有叶节点处于同一级别。所有非叶节点都没有空的子树，并且它们的键数比其子节点数少1。

B树上执行的操作 (Operations performed on B Tree)

Insertion in B-Tree
插入B树
Deletion from B-Tree
从B树删除

1)插入B树 (1) Insertion in B-Tree)

The insertion of a key in a B tree requires the first traversal in B-tree. Through the traversal, it is easy to find that key which needs to be inserted is already existed or not. There are basically two cases for inserting the key that are:

在B树中插入密钥需要在B树中进行第一次遍历。通过遍历，很容易发现需要插入的密钥已经存在或不存在。基本上有两种插入密钥的情况：

Node is not full
节点未满
Node is already full
节点已满

If the leaf node in which the key is to be inserted is not full, then the insertion is done in the node.

如果要插入密钥的叶节点未满，则在该节点中完成插入。

If the node were to be full then insert the key in order into existing set of keys in the node, split the node at its median into two nodes at the same level, pushing the median element up by one level.

如果节点已满，则按顺序将密钥插入节点中现有的密钥集中，将节点的中值拆分为同一级别的两个节点，将中值元素向上推一个级别。

Let us take a list of keys and create a B-Tree: 5,9,3,7,1,2,8,6,0,4

让我们获取一个键列表并创建一个B树：5,9,3,7,1,2,8,6,0,4

1) Insert 5

1)插入5

2) Insert 9: B-tree insert simply calls B tree insert non-full, putting 9 to the right of 5.

2)插入9 ：B树插入简单地调用B树插入不完整，将9放在5的右边。

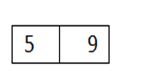
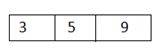
3) Insert 3: Again B-tree insert non-full is called

3)插入3 ：再次调用非完整的B树插入

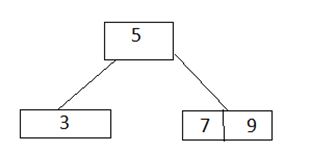
4) Insert 7: Tree is full. We allocate a new empty node, make it the root, split a former root, and then pull 5 into a new root.

4)插入7 ：树已满。我们分配一个新的空节点，将其设为根，拆分先前的根，然后将5拉入新的根。

5) Insert 1: It goes with 3

5)插入1 ：与3对应

6) Insert 2: It goes with 3

6)插入2 ：与3对应

7) Insert 8, 6: As firstly 8 goes with the 9 and then 6 would go with 7, 8, 9 but that node is full. So we split it bring its middle child into the root.

7)插入8、6 ：首先8与9并存，然后6与7、8、9并存，但该节点已满。因此，我们将其拆分为中间孩子。

8) Insert 0, 4: 0 would go with the 1, 2, and 3 which are full, so we split it sending the middle child up to the root. Now it would be nice to just stick 4 in with 3, but the B-tree algorithm requires us to split the full root. Now we can insert 4 assured that future insertion will work.

8)插入0、4 ：0将与1、2和3充满，因此我们将其拆分，将中间子级发送到根。现在将4和3坚持下去会很好，但是B树算法要求我们拆分完整的根。现在我们可以插入4，确保将来的插入将起作用。

2)从B树删除 (2) Deletion from B Tree)

Deletion of the key also requires the first traversal in B tree, after reaching on a particular node two cases may be occurred that are:

删除密钥还需要在B树中进行第一次遍历，到达特定节点后可能会发生两种情况：

Node is leaf node
节点是叶节点
Node is non leaf node
节点是非叶节点

Example: Let us take a B tree of order 5

示例：让我们采用5阶B树

1) Delete 190: Here 190 is in leaf node, so delete it from only leaf node.

1)删除190 ：此处的190位于叶节点中，因此仅从叶节点中将其删除。

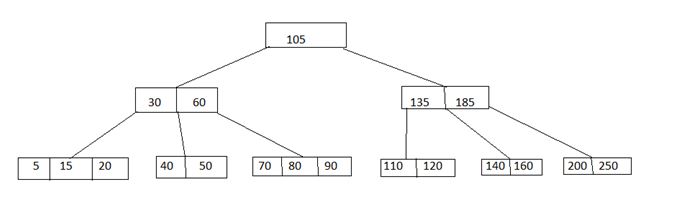
2) Delete 60: Here 60 is in non leaf node. So first it will be deleted from the node and then the element of the right child will come in that node.

2)删除60 ：这里60在非叶节点中。因此，首先将其从节点中删除，然后右子元素将进入该节点。

B树的应用 (Applications of B Tree)

The main application of a B tree is the organization of a huge collection of a data into a file structure. In this insertion, deletion and modification can be carried out perfectly and efficiently.

B树的主要应用是将庞大的数据集合组织到文件结构中。通过这种插入，可以完美而有效地进行删除和修饰。

Full, so we split it sending the middle child up to the root. Now it would be nice to just stick 4 in with 3, but the B-tree algorithm requires us to split the full root. Now we can insert 4 assured that future insertion will work.

已满，因此我们将其拆分，将中间孩子发送到根。现在将4和3坚持下去会很好，但是B树算法要求我们拆分完整的根。现在我们可以插入4，确保将来的插入将起作用。