霍夫码编码（一种不等长，非前缀编码方式）

霍夫曼编码是一种不等长非前缀编码方式，于1951年由MIT的霍夫曼提出。
用于对一串数字/符号编码获取最短的结果，获取最大的压缩效率。
特点：不等长、非前缀

等长式编码

等长编码，意思是对出现的元素采用相同位数的序号进行标定，如下列所示：(这里我们采用三位)

假设有这样一串数据：

编码后的数据量：12 x 3bit=36bit.
思考：对5个数编码没必要每个数是同样的长度，只要五个字符对应的五个编码各自具有可区分性就行了。
非等长编码就是对不同的字符进行不同长度的编码

非等长式编码

如下列所示，我们采用非等长编码：

拿刚才说的字符串举例：

编码后的数据量是：3x2+1x5+2x3+41+14=25bit.
数据量减少了。
思考：如何确定哪种字符使用比较长的编码，哪种字符使用比较短的编码？
出现次数越多的字符我们使用更加短的编码，出现次数越少的字符我们使用更加长的编码。
现在可能又有疑问：为何不能像这样，B=0,A=1,类似这样，我们可以获取更加短的编码。
这里就要说到霍夫曼编码的另外一个特性：非前缀编码。

非前缀编码

以下图为例：

任何一个数据的编码都不与其他数据的编码的前缀重复。
如果B的编码为1，则和其他编码的前缀重复。
又如，C为11的话就和A、D、E的前缀重复了。
非前缀编码的优点：
在编码的时候其实和前缀编码一样，并没有什么简化的步骤。
但是在解码的时候将会有不同的效果：
假设，我们现在有一串数据：

解码得：
1110 110 1111 0 10 0 110 10 0 0 0 10
D A E B C B A C B B B C
已知码表，对编码后的信息进行解码，不需要知道断位信息，即可解码。也就是说我们不需要知道哪几个字符属于同一个就可以进行解码.

前缀编码

假设编码方式为如下。
前缀编码
当获取的数据串是：

在不知道断位信息的前提下，我们是无法对这串数据进行编码的。

霍夫曼编码

霍夫曼编码提供一种自动的方式获取非前缀非等长的编码，通过二叉树进行编码。

1）将信源符号的概率按减小的顺序排队。
2）把两个最小的概率相加，并继续这一步骤，始终将较高的概率分支放在右边，直到最后变成概率１。
3）画出由概率１处到每个信源符号的路径，顺序记下沿路径的０和１，所得就是该符号的霍夫曼码字。
4）将每对组合的左边一个指定为0，右边一个指定为1（或相反）。

例子讲解：
1、计算每个字符出现次数

input	出现次数
B	10
A	8
C	3
D	4
E	5

2、把出现次数（概率）最小的两个相加，并作为左右子树，重复此过程，直到概率值为1

第一次：将概率最低值3和4相加，组合成7：

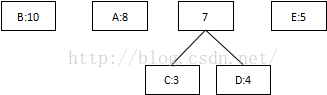
第二次：将最低值5和7相加，组合成12：

第三次：将8和10相加，组合成18：

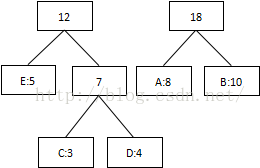
第四次：将最低值12和18相加，结束组合：

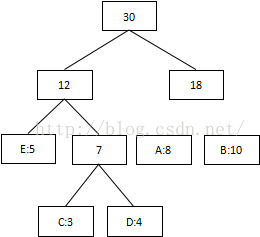
3 将每个二叉树的左边指定为0，右边指定为1

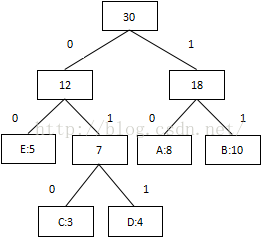
4 沿二叉树顶部到每个字符路径，获得每个符号的编码

output	编码
B	11
A	10
C	010
D	011
E	00

霍夫曼编码的缺陷：

（1）哈夫曼编码所形成的码字不是复唯一的，但编码效率是唯一的在对最小的两个概率符号赋值时，可以规定为大的为“1”、小的为“0”，反之也可以。如果两个符号的出现概率相等时，排列时无论哪个在前都是可以的，所以哈夫曼所构造的码字不是唯一的，对于制同一个信息源，无论上述的前后顺序如何排列，它的平均码长是不会改变的，所以编码效率是唯一的。
（2）只有当信息源各符号出现的概率很不平百均的时候，哈夫曼编码的效果才明显。
（3）哈夫曼编码必须精确地统度计出原始文件中每个符号的出现频率，如果没有这些精确的统计，将达不到预期的压缩效果。霍夫曼编通常要经过两遍操作，第一遍进行统计，第二遍产生编码，所以编码速度相对慢。另外实现的电路复杂，各问种长度的编码的译码过程也是较复杂的，因此解压缩的过程也比较慢。
（4）哈夫曼编码只能用整数来表示单个符号而不能用小数，这很大程度上限制了压缩效果。
（5）哈夫曼所有位都是合在一起的，如果改动其中一位就可以答使其数据变得面目全非

编程实现

代码摘自博客：霍夫曼编码（Huffman Coding）

#include <stdio.h>
#include<stdlib.h>
#include<string>
#include <iostream>#define MAXBIT      100
#define MAXVALUE  10000
#define MAXLEAF     30
#define MAXNODE    MAXLEAF*2 -1typedef struct 
{int bit[MAXBIT];int start;
} HCodeType;        /* 编码结构体 */
typedef struct
{int weight;int parent;int lchild;int rchild;char value;
} HNodeType;        /* 结点结构体 *//* 构造一颗哈夫曼树 */
void HuffmanTree (HNodeType HuffNode[MAXNODE],  int n)
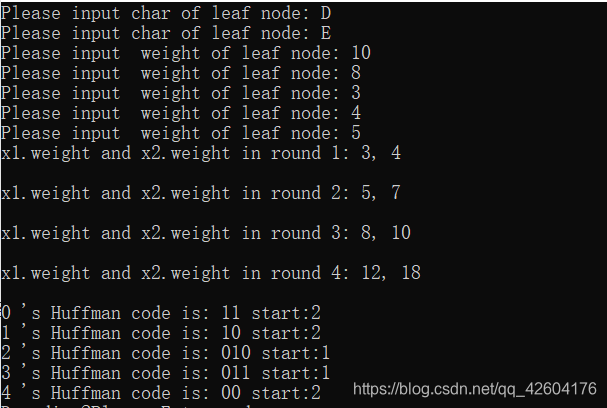
{ /* i、j： 循环变量，m1、m2：构造哈夫曼树不同过程中两个最小权值结点的权值，x1、x2：构造哈夫曼树不同过程中两个最小权值结点在数组中的序号。*/int i, j, m1, m2, x1, x2;/* 初始化存放哈夫曼树数组 HuffNode[] 中的结点 */for (i=0; i<2*n-1; i++){HuffNode[i].weight = 0;//权值 HuffNode[i].parent =-1;HuffNode[i].lchild =-1;HuffNode[i].rchild =-1;HuffNode[i].value=' '; //实际值，可根据情况替换为字母  } /* end for *//* 输入 n 个叶子结点的权值 */for (i=0; i<n; i++){printf ("Please input char of leaf node: ", i);scanf ("%c",&HuffNode[i].value);getchar();} /* end for */for (i=0; i<n; i++){printf ("Please input  weight of leaf node: ", i);scanf ("%d",&HuffNode[i].weight);getchar();} /* end for *//* 循环构造 Huffman 树 */for (i=0; i<n-1; i++){m1=m2=MAXVALUE;     /* m1、m2中存放两个无父结点且结点权值最小的两个结点 */x1=x2=0;/* 找出所有结点中权值最小、无父结点的两个结点，并合并之为一颗二叉树 */for (j=0; j<n+i; j++){if (HuffNode[j].weight < m1 && HuffNode[j].parent==-1){m2=m1; x2=x1; m1=HuffNode[j].weight;x1=j;}else if (HuffNode[j].weight < m2 && HuffNode[j].parent==-1){m2=HuffNode[j].weight;x2=j;}} /* end for *//* 设置找到的两个子结点 x1、x2 的父结点信息 */HuffNode[x1].parent  = n+i;HuffNode[x2].parent  = n+i;HuffNode[n+i].weight = HuffNode[x1].weight + HuffNode[x2].weight;HuffNode[n+i].lchild = x1;HuffNode[n+i].rchild = x2;printf ("x1.weight and x2.weight in round %d: %d, %d\n", i+1, HuffNode[x1].weight, HuffNode[x2].weight);  /* 用于测试 */printf ("\n");} /* end for */} /* end HuffmanTree *///解码 
void decodeing(char string[],HNodeType Buf[],int Num)
{int i,tmp=0,code[1024];int m=2*Num-1;char *nump;char num[1024];for(i=0;i<strlen(string);i++){if(string[i]=='0')num[i]=0;        elsenum[i]=1;                    } i=0;nump=&num[0];while(nump<(&num[strlen(string)])){tmp=m-1;while((Buf[tmp].lchild!=-1)&&(Buf[tmp].rchild!=-1)){if(*nump==0){tmp=Buf[tmp].lchild ;          } else tmp=Buf[tmp].rchild;nump++;} printf("%c",Buf[tmp].value);                                  }
}int main(void)
{HNodeType HuffNode[MAXNODE];            /* 定义一个结点结构体数组 */HCodeType HuffCode[MAXLEAF],  cd;       /* 定义一个编码结构体数组， 同时定义一个临时变量来存放求解编码时的信息 */int i, j, c, p, n;char pp[100];printf ("Please input n:\n");scanf ("%d", &n);HuffmanTree (HuffNode, n);for (i=0; i < n; i++){cd.start = n-1;c = i;p = HuffNode[c].parent;while (p != -1)   /* 父结点存在 */{if (HuffNode[p].lchild == c)cd.bit[cd.start] = 0;elsecd.bit[cd.start] = 1;cd.start--;        /* 求编码的低一位 */c=p;                    p=HuffNode[c].parent;    /* 设置下一循环条件 */} /* end while *//* 保存求出的每个叶结点的哈夫曼编码和编码的起始位 */for (j=cd.start+1; j<n; j++){ HuffCode[i].bit[j] = cd.bit[j];}HuffCode[i].start = cd.start;} /* end for *//* 输出已保存好的所有存在编码的哈夫曼编码 */for (i=0; i<n; i++){printf ("%d 's Huffman code is: ", i);for (j=HuffCode[i].start+1; j < n; j++){printf ("%d", HuffCode[i].bit[j]);}printf(" start:%d",HuffCode[i].start);printf ("\n");}printf("Decoding?Please Enter code:\n");scanf("%s",&pp);decodeing(pp,HuffNode,n);getchar();return 0;
}