题目

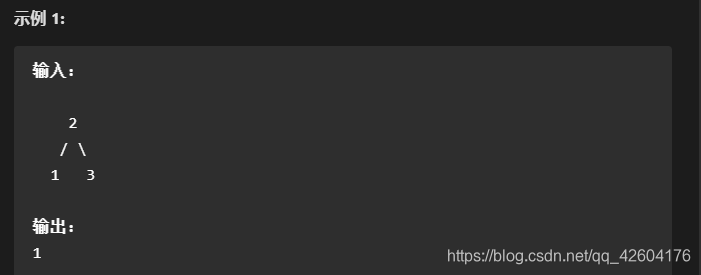
给定一个二叉树，在树的最后一行找到最左边的值。

递归解

左下角要满足两个条件：
1、深度最大的叶子结点
2、最左结点：使用前序遍历，优先左边搜索。
1、确定递归函数的参数和返回值
参数：树的根结点，maxlen记录最大深度,maxleftval记录最大深度最左结点的数值。

int maxlen = 0;		//全局变量，记录最大深度
int maxleftval;		//全局变量 最大深度最左节点的数值
void traversal(TreeNode* root,int leftlen);

2、确定终止条件
遇到叶子结点，统计一下最大深度

if(root->left == NULL && root->right == NULL)
{if(leftlen > maxlen)		//如果是同一深度则不会进行更新数值{maxlen=leftlen;		//更新最大深度maxleftval = root->val;		//最大深度最左边的数值}return ;
}

3、确定单层逻辑
和之前的思路一样，在找最大深度的时候，递归过程中依然要使用回溯

//中，不需要操作
if(root->left)
{leftlen++;	//深度+1traversal(root->left,leflen);leftlen--;	//回溯，深度-1
}
if(root->right)
{leftlen++;	//深度+1traversal(root->right,leflen);leftlen--;	//回溯，深度-1
}
return ;

完整代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:int maxlen = -1;		//全局变量，记录最大深度int maxleftval;		//全局变量 最大深度最左节点的数值void traversal(TreeNode* root,int leftlen){if(root->left == NULL && root->right == NULL){if(leftlen > maxlen)		//如果是同一深度则不会进行更新数值{maxlen=leftlen;		//更新最大深度maxleftval = root->val;		//最大深度最左边的数值}return ;}//中，不需要操作if(root->left){leftlen++;	//深度+1traversal(root->left,leftlen);leftlen--;	//回溯，深度-1}if(root->right){leftlen++;	//深度+1traversal(root->right,leftlen);leftlen--;	//回溯，深度-1}return ;}int findBottomLeftValue(TreeNode* root) {traversal(root,0);return maxleftval;}
};

如果需要遍历整棵树，递归函数就不能有返回值。如果需要遍历某一条固定路线，递归函数就一定要有返回值

层序遍历解

层序遍历，将每层第一个元素赋值给一个变量result。遍历所有层，最后的result就是结果

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:int findBottomLeftValue(TreeNode* root) {int result=0;queue<TreeNode*> que;if(root!=NULL) que.push(root);while(!que.empty()){//该层结点元素个数 = 该层队列元素int size = que.size();//这里要使用固定大小的size，不能使用que.size(),因为在处理中que.size是不断变化的//将这层元素送入队列中并依次从队首向队尾将元素出队列，每个元素出队列的同时又将其不为空的子结点送入队列for(int i =0;i<size;i++){if(i==0) result = que.front()->val;TreeNode* node = que.front();//将队首元素送入该层结果que.pop();//将左右孩子结点入队列，作为下一层的元素if(node->left) que.push(node->left);if(node->right) que.push(node->right);}}return result;}
};