leetcode 106. 从中序与后序遍历序列构造二叉树 105. 从前序与中序遍历序列构造二叉树思考分析

目录

    • 1、106题目
    • 2、参考思路：递归切割数组
    • 3、105题目
    • 4、同样思路的代码

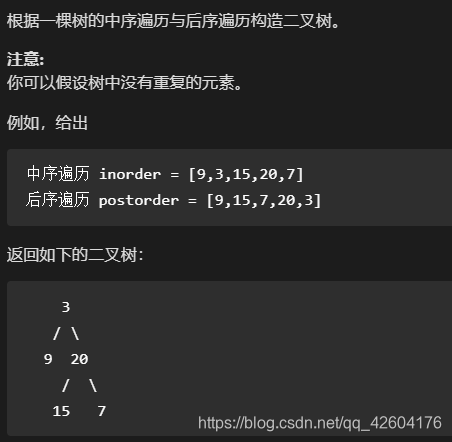
1、106题目

在这里插入图片描述

2、参考思路：递归切割数组

代码参考：公众号：代码随想录
后序数组+中序数组
以 后序数组(左右中)的最后一个元素作为切割点，先切中序数组，根据中序数组反过来再切割后序数组。一层一层切割下去，每次后序数组最后一个元素就是结点元素。
先序数组+中序数组
以 先序数组(中左右)的第一个元素作为切割点，先切中序数组，根据中序数组反过来再切割先序数组。一层一层切割下去，每次先序数组第一个元素就是结点元素。
先序数组+后序数组为何不能构造一个唯一的二叉树
对于一个二叉树，并不是说给出了先序和后序就是无法唯一确定的。只是说，在某些情况下，不能唯一确定。
即：

当二叉树中某个节点仅仅只有一个孩子节点的时候，就无法根据其先序和后序唯一的确定一个二叉树。
更详细的解释请看这个链接:
关于二叉树先序遍历和后序遍历为什么不能唯一确定一个二叉树分析
我的理解：由于中序遍历的存在，你只需要找到中间结点就可以十分迅速并且准确地确定它的左右孩子，而后序、前序遍历则没有这个特征。
举例：给定序列1 2 3 4，且中间结点是3。
中序遍历，则可得到：1、2是3结点的左子树的结点、4是3结点的右子树的结点
给定序列1 2 3 4，且中间结点是1。
先序遍历，你不知道234三个结点究竟是怎样分布在左右子树上的，可能是：
【234】【】；
【23】【4】；
【2】【34】；
【】【234】；
后序遍历同理。

递归分析：

1、如果数组大小为0的话，说明就是空结点。
2、如果不为空，那么取后序数组最后一个元素作为结点元素
3、找到后序数组最后一个元素在中序数组的位置，作为切割点
4、切割中序数组，切割成中序左数组和中序右数组
5、切割后序数组，切成后序左数组和后序右数组
6、递归处理左区间和右区间

关于构造二叉树的方法，回顾;
LintCode 375. 克隆二叉树(深复制)

TreeNode* traversal(vector<int>& inorder, vector<int>& postorder) {//step1if(postorder.size() == 0 ) return NULL;//step2:后序遍历数组的最后一个元素就是当前的中间结点int rootVal = postorder[postorder.size()-1];TreeNode* NewRoot = new TreeNode(rootVal);//如果是叶子结点，返回结点if(postorder.size() == 1) return NewRoot;//step3：寻找切割点int CutIndex ;for(CutIndex=0;CutIndex<inorder.size();CutIndex++){if(inorder[CutIndex] == rootVal) break;}//step4:切割中序数组，得到中序左数组和中序右数组//step5:切割后序数组，得到后序左数组和后序右数组//step6：/*root->left = traversal(中序左数组,后序左数组);root->left = traversal(中序右数组,后序右数组);*/}

切割的原则我们遵循左闭右开(右边的不取).
切割中序数组

//找到中序遍历的切割点
int CutIndex ;
for(CutIndex=0;CutIndex<inorder.size();CutIndex++)
{if(inorder[CutIndex] == rootVal) break;
}
//区间形式：[x1,x2);
vector<int> leftInorder(inorder.begin(),inorder.begin()+CutIndex );
vector<int> rightInorder(inorder.begin()+CutIndex+1,inorder.end() );

切割后序数组
1、后序数组没有明确的切割元素来进行左右切割。
2、中序数组的大小和后序数组的大小相同。
3、我们已经将中序数组切割成了左、右两个子数组了。
4、舍弃掉后序数组末尾元素，因为这个元素是中间结点

//舍弃末尾元素
postorder.resize(postorder.size() -1 );
//左闭右开，使用了左中序数组大小作为切割点：[0,leftorder.size()]
vector<int> leftPostorder(postorder.begin(),postorder.begin()+leftInorder.size());
vector<int> rightPostorder(postorder.begin()+leftInorder.size(),postorder.end());

接下来是递归

root->left = traversal(leftInorder,leftPostorder);
root->right= traversal(rightInorder,rightPostorder);

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:TreeNode* traversal(vector<int>& inorder, vector<int>& postorder) {//step1if(postorder.size() == 0 ) return NULL;//step2:后序遍历数组的最后一个元素就是当前的中间结点int rootVal = postorder[postorder.size()-1];TreeNode* NewRoot = new TreeNode(rootVal);//如果是叶子结点，返回结点if(postorder.size() == 1) return NewRoot;//step3：寻找切割点int CutIndex ;for(CutIndex=0;CutIndex<inorder.size();CutIndex++){if(inorder[CutIndex] == rootVal) break;}//step4:切割中序数组，得到中序左数组和中序右数组//区间形式：[x1,x2);vector<int> leftInorder(inorder.begin(),inorder.begin()+CutIndex );vector<int> rightInorder(inorder.begin()+CutIndex+1,inorder.end() );//step5:切割后序数组，得到后序左数组和后序右数组//舍弃末尾元素postorder.resize(postorder.size() -1 );//左闭右开，使用了左中序数组大小作为切割点：[0,leftorder.size()]vector<int> leftPostorder(postorder.begin(),postorder.begin()+leftInorder.size());vector<int> rightPostorder(postorder.begin()+leftInorder.size(),postorder.end());//step6：NewRoot->left = traversal(leftInorder,leftPostorder);NewRoot->right= traversal(rightInorder,rightPostorder);return NewRoot;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if(inorder.size() == 0 || postorder.size() == 0) return NULL;return traversal(inorder,postorder);}
};

分析：每层递归都定义了数组，耗时间也耗空间。
下面给出用下标索引分割代码，不需要重新构造数组了。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:
// 中序区间：[inorderBegin, inorderEnd)，后序区间[postorderBegin, postorderEnd)TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {if (postorderBegin == postorderEnd) return NULL;int rootValue = postorder[postorderEnd - 1];TreeNode* root = new TreeNode(rootValue);if (postorderEnd - postorderBegin == 1) return root;int delimiterIndex;for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;}// 切割中序数组// 左中序区间，左闭右开[leftInorderBegin, leftInorderEnd)int leftInorderBegin = inorderBegin;int leftInorderEnd = delimiterIndex;// 右中序区间，左闭右开[rightInorderBegin, rightInorderEnd)int rightInorderBegin = delimiterIndex + 1;int rightInorderEnd = inorderEnd;// 切割后序数组// 左后序区间，左闭右开[leftPostorderBegin, leftPostorderEnd)int leftPostorderBegin =  postorderBegin;int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size// 右后序区间，左闭右开[rightPostorderBegin, rightPostorderEnd)int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素，已经作为节点了root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  postorder, leftPostorderBegin, leftPostorderEnd);root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if(inorder.size() == 0 || postorder.size() == 0) return NULL;return traversal(inorder,0,inorder.size(),postorder,0,postorder.size());}
};

3、105题目

在这里插入图片描述

4、同样思路的代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:
// 中序区间：[inorderBegin, inorderEnd)，先序区间[preorderBegin, preorderEnd)TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {if (preorderBegin == preorderEnd) return NULL;int rootValue = preorder[preorderBegin];TreeNode* root = new TreeNode(rootValue);if (preorderEnd - preorderBegin == 1) return root;int delimiterIndex;for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;}// 切割中序数组// 左中序区间，左闭右开[leftInorderBegin, leftInorderEnd)int leftInorderBegin = inorderBegin;int leftInorderEnd = delimiterIndex;// 右中序区间，左闭右开[rightInorderBegin, rightInorderEnd)int rightInorderBegin = delimiterIndex + 1;int rightInorderEnd = inorderEnd;// 切割先序数组// 左先序区间，左闭右开[leftPreorderBegin, leftPreorderEnd)int leftPreorderBegin =  preorderBegin + 1;// 排除第一个元素，已经作为节点了int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size// 右先序区间，左闭右开[rightPreorderBegin, rightPreorderEnd)int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);int rightPreorderEnd = preorderEnd;  root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  preorder, leftPreorderBegin, leftPreorderEnd);root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if(inorder.size() == 0 || preorder.size() == 0) return NULL;return traversal(inorder,0,inorder.size(),preorder,0,preorder.size());}
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/377959.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

二十、分水岭算法

二十、分水岭算法

一、基本原理 分水岭算法主要是基于距离变换&#xff08;distance transform&#xff09;&#xff0c;找到mark一些种子点&#xff0c;从这些种子点出发根据像素梯度变化进行寻找边缘并标记 分水岭&#xff1a;可以简单的理解成一座山&#xff0c;然后来洪水了&#xff0c;水开…
阅读更多...
【C++grammar】C++类数据成员的初始化

【C++grammar】C++类数据成员的初始化

目录1、类成员的就地初始化example2、构造函数初始化3、默认构造函数&#xff1a;Default Constructor4、举例5、成员的初始化方法的优先级1、类成员的就地初始化example class S { int m 7; // ok, copy-initializes m int n(7); // 错误&#xff1a;不允许用小括号初始化…
阅读更多...
二十一、人脸检测

二十一、人脸检测

一、识别图像中的人脸 haarcascade_frontalface_alt_tree.xml lbpcascade_frontalcatface.xml GitHub上有Haar级联检测器源代码可自行下载&#xff0c;lbp级联检测器也一样有源码可自行下载 也一样 import cv2 as cv import numpy as npdef face_detect(image):gray cv.cvtC…
阅读更多...
javascript运算符_JavaScript中的按位运算符

javascript运算符_JavaScript中的按位运算符

javascript运算符JavaScript按位运算符 (JavaScript Bitwise Operators) A lot of times you come across some strange operators where youre knocking your head to understand what is going on in the code. Almost all the programming languages have bitwise operators…
阅读更多...
[置顶] Android的IPC访问控制设计与实现

[置顶] Android的IPC访问控制设计与实现

3.3.1 IPC钩子函数设计与实现 IPC Binder是Android最重要的进程间通信机制&#xff0c;因此&#xff0c;必须在此实施强制访问控制。 1. 修改secuirty.h 打开终端shell&#xff0c;输入指令“cd /android4.0/kernel/goldfish/include/linux/vim security.h”&#xff0c;找到结…
阅读更多...
TensorFlow在Anaconda环境下创建

TensorFlow在Anaconda环境下创建

一、我使用的是Anaconda自带的Jupyter编译器&#xff0c;详细的安装教程可以参考博文 二、之后打开Jupyter 三、进行测试 我的tensorflow使用的是2.0版本 import tensorflow.compat.v1 as tf tf.disable_v2_behavior()a tf.constant([1.0,2.0],name"a") b tf.co…
阅读更多...
leetcode 654. 构造最大二叉树 思考分析

leetcode 654. 构造最大二叉树 思考分析

题目 给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下&#xff1a; 二叉树的根是数组中的最大元素。 左子树是通过数组中最大值左边部分构造出的最大二叉树。 右子树是通过数组中最大值右边部分构造出的最大二叉树。 通过给定的数组构建最大二叉树&am…
阅读更多...
Pycharm更换anaconda环境空间

Pycharm更换anaconda环境空间

一、File—>Settings 或者直接快捷键 CtrlAltS 二、找到自己的项目—>Project Interpreter—>找到需要使用的anaconda环境空间 三、Add Local 四、G:\Anaconda3\envs\mask_rcnn\python.exe一般anaconda的envs文件夹下&#xff0c;找到你的环境空间名称&#xff0c;…
阅读更多...
android 应用demo截图

android 应用demo截图

ksoap2实现天气预报 Frame 动画 baidu map 转载于:https://www.cnblogs.com/java20130726/archive/2011/11/28/3218328.html
阅读更多...
leetcode 617. 合并二叉树 思考分析

leetcode 617. 合并二叉树 思考分析

题目 给定两个二叉树&#xff0c;想象当你将它们中的一个覆盖到另一个上时&#xff0c;两个二叉树的一些节点便会重叠。 你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠&#xff0c;那么将他们的值相加作为节点合并后的新值&#xff0c;否则不为 NULL 的节点…
阅读更多...
如何关掉Microsoft Office Click-to-Run服务

如何关掉Microsoft Office Click-to-Run服务

很烦&#xff0c;一开电脑就出现 一、打开任务管理器(CtrlShiftEsc) 服务—>打开服务 二、找到Microsoft Office Click-to-Run Service 右击&#xff0c;选择属性 三、禁用即可
阅读更多...
友盟—安卓巴士【Android开发原创教程大赛】

友盟—安卓巴士【Android开发原创教程大赛】

Android开发原创教程大赛正式拉开序幕了&#xff0c;由国内最专业的移动开发者服务及统计平台-友盟提供丰厚的话费奖品哦&#xff0c;为所有爱写教程的开发者提供的一份奖励。 活动时间&#xff1a;2011年11月29日——2011年12月21日 征集期&#xff1a;2011年…
阅读更多...
leetcode 700. 二叉搜索树中的搜索 思考分析

leetcode 700. 二叉搜索树中的搜索 思考分析

目录题目1、不考虑BST性质&#xff0c;直接递归遍历2、回顾BST性质3、利用BST性质进行遍历4、简单的迭代方法题目 给定二叉搜索树&#xff08;BST&#xff09;的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在&#xf…
阅读更多...
一、环境准备

一、环境准备

一、前提已安装好anaconda 二、打开cmd命令窗口 conda activate激活base环境 conda create -n pytorch python3.6创建一个名称为pytorch的环境空间&#xff0c;其中使用的python版本为3.6 conda env list查看当前都有哪些环境 conda activate pytorch 激活刚安装的环境 pip l…
阅读更多...
LeetCode 98. 验证二叉搜索树 思考分析

LeetCode 98. 验证二叉搜索树 思考分析

题目 给定一个二叉树&#xff0c;判断其是否是一个有效的二叉搜索树。 假设一个二叉搜索树具有如下特征&#xff1a; 节点的左子树只包含小于当前节点的数。 节点的右子树只包含大于当前节点的数。 所有左子树和右子树自身必须也是二叉搜索树。 1、利用BST性质&#xff1a;中序…
阅读更多...
二、VC++环境的安装

二、VC++环境的安装

一、打开PyCharm 在Terminal中激活pytorch环境&#xff0c;conda activate pytorch 安装pycocotools工具&#xff0c;pip install pycocotools 二、报错需安装VC 进入官网 安装完成之后重启电脑 三、再次安装pycocotools 打开Pycharm&#xff0c;安装pycocotools工具&am…
阅读更多...
LeetCode 530. 二叉搜索树的最小绝对差 思考分析

LeetCode 530. 二叉搜索树的最小绝对差 思考分析

目录题目思路1&#xff1a;递归遍历得到result数组(单调递增)&#xff0c;然后对数组进行前后差分&#xff0c;取最小值思路2&#xff1a;不用数组&#xff0c;进行优化思路3、回顾迭代法求解题目 给你一棵所有节点为非负值的二叉搜索树&#xff0c;请你计算树中任意两节点的差…
阅读更多...
一、线性回归

一、线性回归

一、在有监督学习中主要包括两大类问题 分类问题&#xff1a;你去银行贷款借钱&#xff0c;人家银行会不会借给你&#xff1f;当然只有两种答案&#xff1a;会、不会 回归问题&#xff1a;人家银行能借给你多少钱&#xff1f;是一个具体的值 举个例子&#xff1a;假如你去银行…
阅读更多...
8-18-Exercise

8-18-Exercise

8-18-小练 A.HDU 1172 猜数字 采用枚举~【赤果果的暴力~】 代码&#xff1a; 1 #include <iostream>2 #include <cstdio>3 #include <cstring>4 using namespace std;5 6 int x[111],y[111],s,ss,vis[4],dis[4];7 char a[111][5];8 9 void find(int b,int …
阅读更多...
leetcode 501. 二叉搜索树中的众数 思考分析

leetcode 501. 二叉搜索树中的众数 思考分析

目录题目1、不考虑BTS性质&#xff0c;直接寻找众数集合&#xff08;利用map&#xff09;2、考虑BTS的中序遍历结果性质题目 给定一个有相同值的二叉搜索树&#xff08;BST&#xff09;&#xff0c;找出 BST 中的所有众数&#xff08;出现频率最高的元素&#xff09;。 假定 BS…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023