一、在有监督学习中主要包括两大类问题

分类问题：你去银行贷款借钱，人家银行会不会借给你？当然只有两种答案：会、不会
回归问题：人家银行能借给你多少钱？是一个具体的值
举个例子：假如你去银行贷款，人家银行主要考虑你月薪和年龄这两个因素来决定你的最终的贷款金额。

x0	你的月薪(x1)	你的年龄(x2)	可以给你贷款金额(Y)
1	3000	20	20000
1	8000	28	35000
1	1000	25	10000
1	4000	30	30000
1	12000	20	50000

很显然，人家银行贷给你钱主要看的是你的月薪，其次看的是你的年龄，这两个元素权重不一样。
x1和x2是两个特征，即月薪和年龄，Y是最终的贷款金额。

二、线性拟合

假设θ1是年龄的参数， θ2是工资的参数，因为是两个参数影响，故需要拟合一个平面。
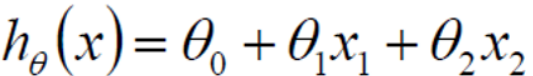，其中θ0是偏置项，方便后续的矩阵操作。
整理得：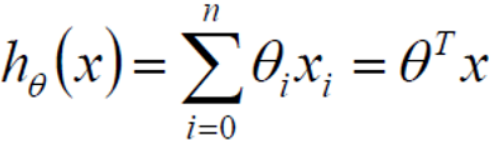

三、误差

真实值和预测值之间肯定存在差异，这个差异就是误差ε。
对于每个样本而言：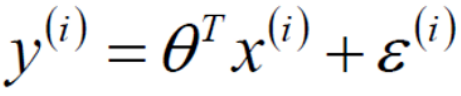

误差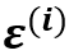，是独立并且具有相同的分布，并且服从均值为0，方差为 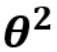的高斯分布。
独立：A和B是两个人，银行对待这两个人是一样的，两个人都不认识，相互独立。
相同的分布：俩人都去同一家银行贷款
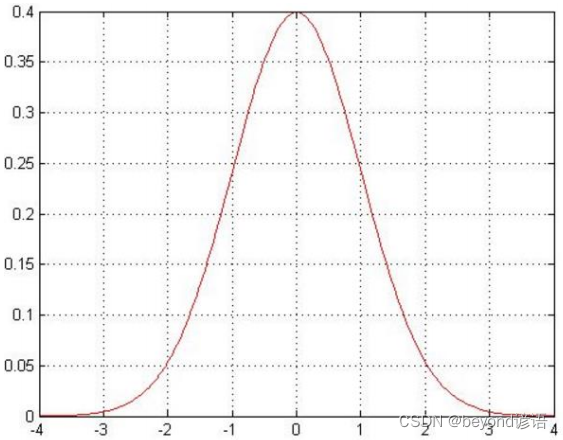
高斯分布：也称正态分布或正常分布。主要是说 银行可能会给的多，也可能给的少，但这都是少数情况，但大多数情况下浮动不会太大，

预测值和误差：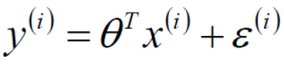
高斯分布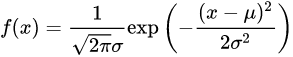：，这里的ε和σ都指代误差。
误差服从高斯分布，带入预测值和误差公式中得：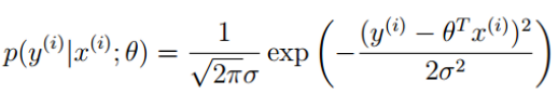

似然函数：这里的均值为0，直接带入简化函数
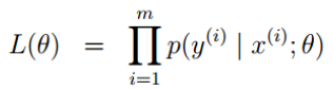
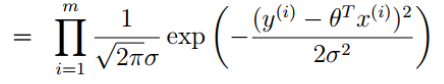，可以理解这个似然函数主要求解什么样的参数(θ0,θ1,θ2)跟我们的数据组合一下可以更好的接近真实值。
但这里是累乘的操作，相比累加而言确实有点麻烦，故需要通过对数似然来将累乘向类和转换。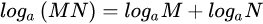

对数似然：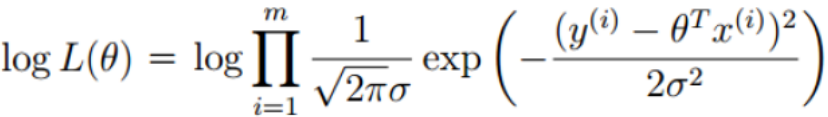
L(θ)和log(θ)的值不同，但这两个函数的极值点θ是一样的，故可以相互等价。

化简：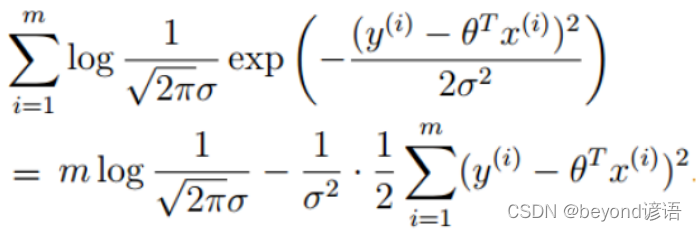
故：最终的目标是让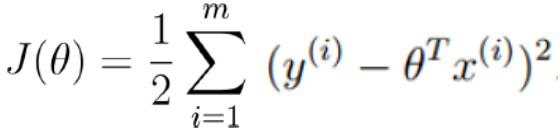取值最小即可。

四、通过最小二乘法求目标函数最小值

目标函数：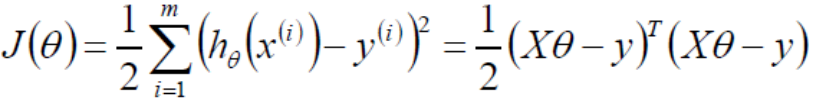
如何求函数最小值？很简单，求导呗，找到导数为0的θ。当然这里是多个变量求的是偏导。

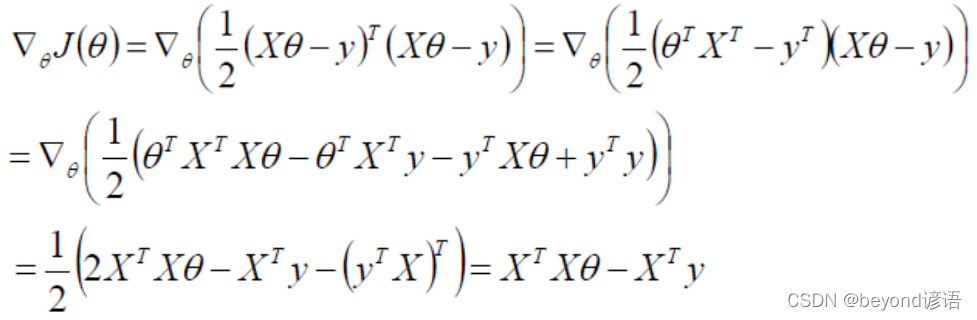
令偏导为0，求出θ即可。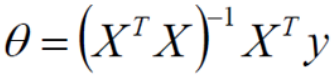

五、评估方法

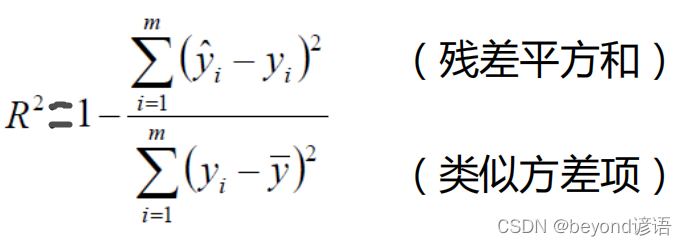
R²越接近于1，则模型拟合的越好。

六、梯度下降法

当我们得到一个目标函数之后，如何求解？你会求解，但是机器学习是让机器去学会这个方法，你学会没用！
故这时候就需要将我们求解的步骤进行具体话，给机器说一下求解的方法、步骤，让机器按照这个步骤来就可以求解出最佳的答案。
对于目标函数：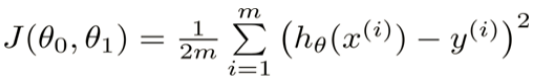

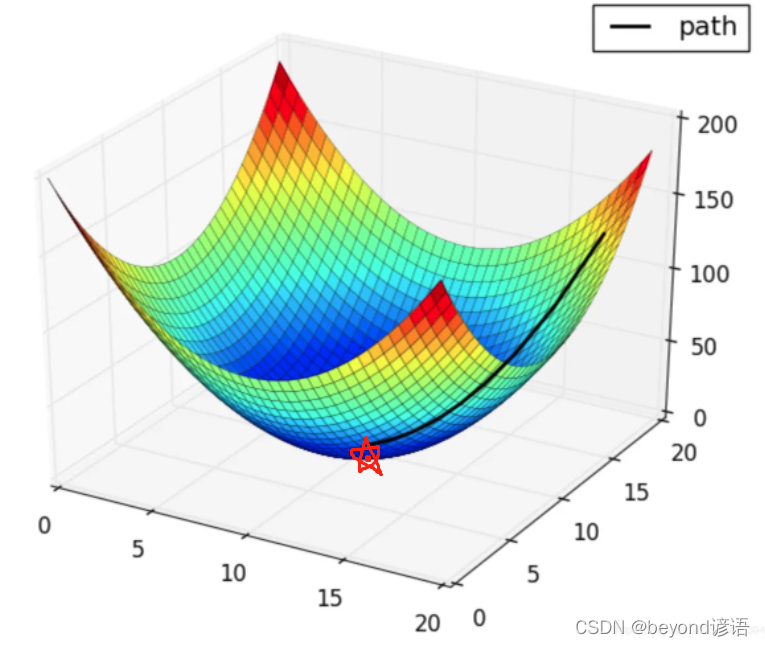
我们的目标是如何找到终点？即什么样的参数能使得目标函数达到极值点

目标函数：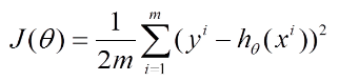
①批量梯度下降：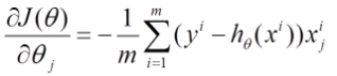
因为这里梯度下降法是沿梯度反方向走的，故需要加个负号，负负得正：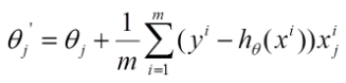
可以看出：容易得到最优解，但是m个样本都考虑到了，速度太慢了。

②随机梯度下降：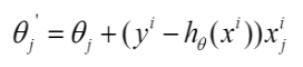
每一次知道一个样本，迭代速度很快，但不一定每次的样本都是收敛的。

③（常用）小批量梯度下降：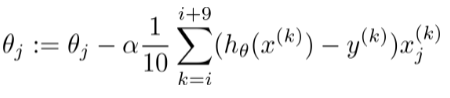
从中随机找几个样本(这里选择10个)，每次更新选择一小部分样本。
这里的α是学习率(learning rate,LR)，也就是每次下降的步长，步长对结果影响很大，一般小一点较好。通常LR=0.01、0.001挨个试试效果。
这里选择的是随机选取10个样本，一般都是随机取64、128、256个样本。

总结梯度下降法步骤：
①分别求每个参数的偏导，找到偏导最小值
②走α步
③按当前方向进行更新参数θ