1、题目
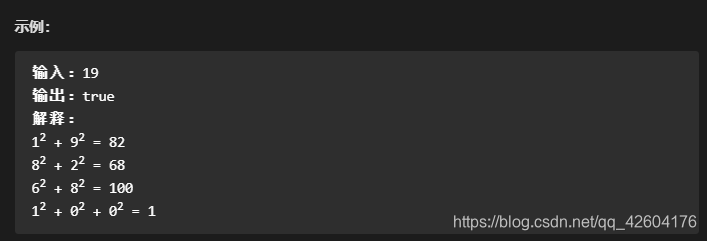
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。如果 可以变为 1,那么这个数就是快乐数。
如果 n 是快乐数就返回 True ;不是,则返回 False 。
2、思考分析
对一个数不断进行get_sum操作,那么最终可能的结果有两种可能:
1、得到1
2、计算的数陷入某种循环,然后会有重复的数出现
如果得到1,直接返回true;
如果检测到重复数出现就返回false;
否则记录出现的数,并在while循环中对n进行更新。
int get_sum(int n)
{int sum=0;while(n!=0){sum+=(n%10)*(n%10);n = n/10;}return sum;}
3、哈希法解
class Solution {
public:int get_sum(int n){int sum=0;while(n!=0){sum+=(n%10)*(n%10);n = n/10;}return sum;}bool isHappy(int n) {int sum=0;//sum,sum出现的频次unordered_set<int> set;while(1){sum=get_sum(n);if(sum ==1) return true;//如果某个数重复出现,那么我们认为此时陷入了循环,则这个数不是快乐数else if(set.find(sum)!=set.end()){return false;}set.insert(sum);n=sum;}}
};
4、双指针解
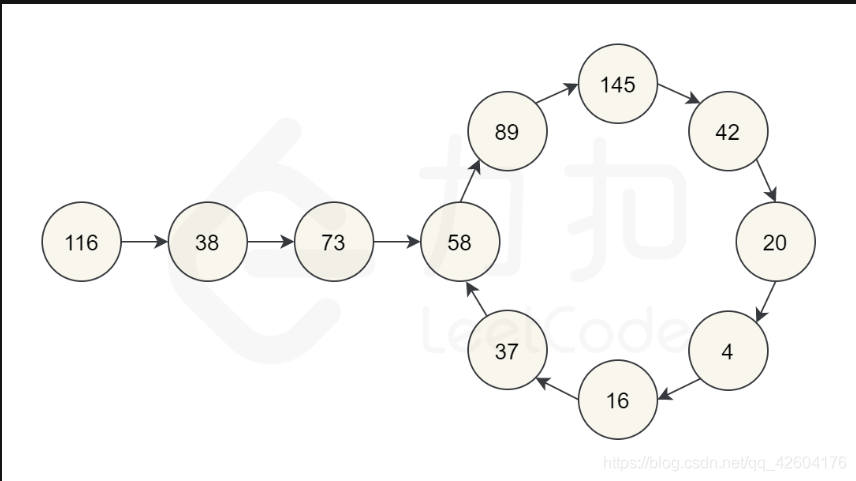
我们得到的结果序列是一个隐式的链表。
隐式意味着我们没有实际的链表节点和指针,但数据仍然形成链表结构。
于是这个问题可以转换为检测一个链表是否有环。
这个问题可以使用快慢指针法来解决。我们不是只跟踪链表中的一个值,而是跟踪两个值,称为快跑者和慢跑者。在算法的每一步中,慢速在链表中前进 1 个节点,快跑者前进 2 个节点。
前进一次调用一次计算函数,前进两次调用两次计算函数。
class Solution {
public:int get_next(int n){int sum=0;while(n!=0){sum+=(n%10)*(n%10);n = n/10;}return sum;}bool isHappy(int n) {int sum=0;int slow_runner = n;int fast_runner = get_next(n);while( fast_runner != 1 && slow_runner != fast_runner){//更新slow_runner,slow_runner每次前进一步slow_runner = get_next(slow_runner);//更新fast_runner,fast_runner每次前进二步,所以调用两次getnext函数fast_runner = get_next(get_next(fast_runner));}if(fast_runner == 1) return true;return false;}
};


)






---讲解)





---小练习)



方法与示例)