博主联系方式:
QQ:1540984562
QQ交流群:892023501
群里会有往届的smarters和电赛选手,群里也会不时分享一些有用的资料,有问题可以在群里多问问。
目录
- 层次分析法的思想
- 层次分析法步骤
- 具体案例(市政工程项目建设决策)
- 1.问题提出
- 2.建立递阶层次结构
- 3.构造判断矩阵(成对比较阵)并赋值
- 4.层次单排序(计算权向量)与检验(一致性检验)
- 计算权向量
- 一致性检验
- 5.层次总排序(组合权向量)与检验(一致性检验)
- 6.结果分析
- 7.层次分析法的优缺点
- 层次分析法的代码实现(matlab)
层次分析法的思想
层次分析法的思想:将所有要分析的问题层次化;
根据问题的性质和所要到达的总目标,将问题分为不同的组成因素,并按照这些因素间的关联影响即其隶属关系,将因素按不同层次聚集组合,形成一个多层次分析结构模型;
最后,对问题进行优劣比较排序.
层次分析法步骤
1、找准各因素之间的隶属度关系,建立递阶层次结构
2、构造判断矩阵,并赋值
3、层次单排序(计算权向量)与检验(一致性检验)
4、层次总排序(组合权向量)与检验(一致性检验)
5、结果分析
具体案例(市政工程项目建设决策)
1.问题提出
市政部门管理人员需要对修建一项市政工程项目进行决策,可选择的方案是修建通往旅游区的高速路(简称建高速路)或修建城区地铁(简称建地铁)。除了考虑经济效益外,还要考虑社会效益、环境效益等因素,即是多准则决策问题,考虑运用层次分析法解决。
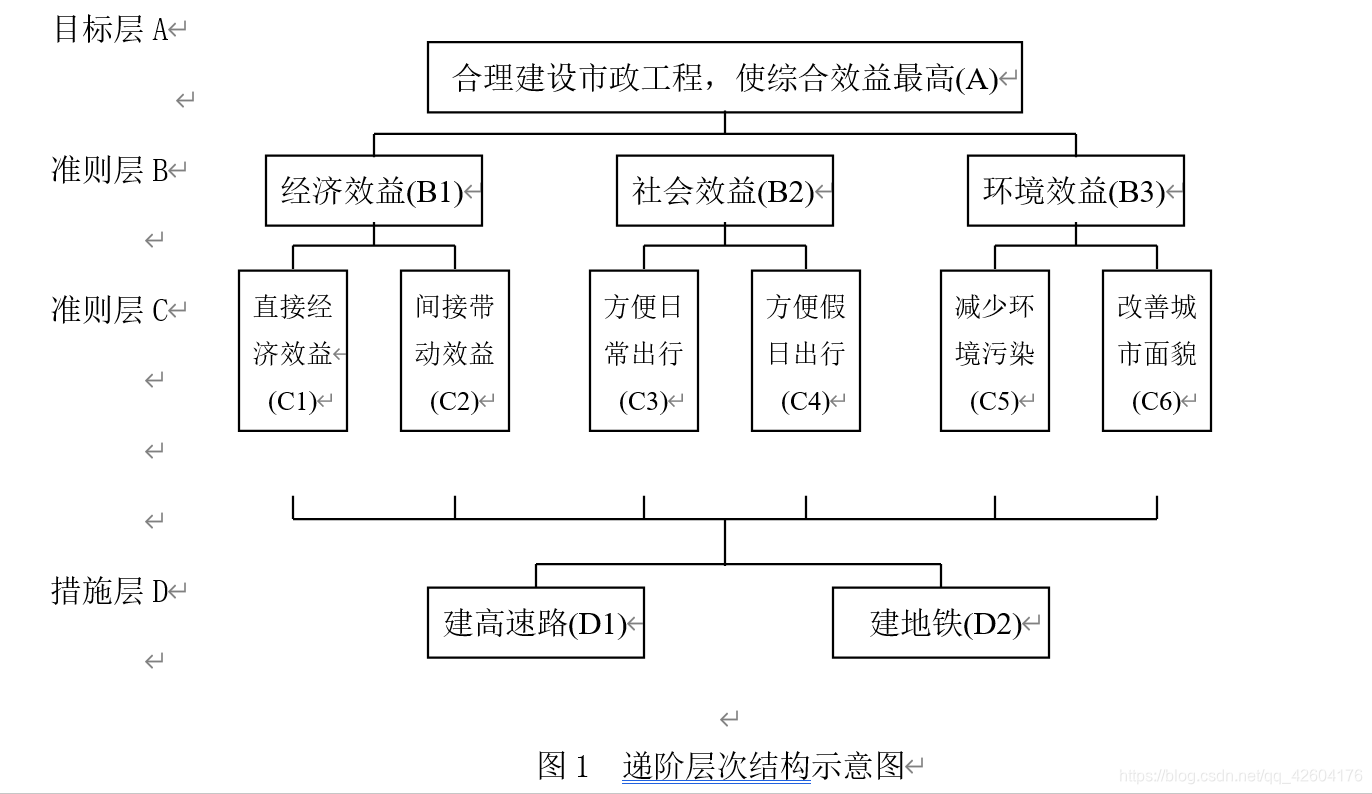
2.建立递阶层次结构
1、明确决策目标:“合理建设市政工程,使综合效益最高”。
2、为了实现这一目标,需要考虑的主要准则有三个,即经济效益、社会效益和环境效益。
还必须考虑直接经济效益、间接经济效益、方便日常出行、方便假日出行、减少环境污染、改善城市面貌等因素(准则),从相互关系上分析,这些因素隶属于主要准则,因此放在下一层次考虑,并且分属于不同准则。
3、解决方案,即建高速路或建地铁,这两个因素作为措施层元素放在递阶层次结构的最下层。
这样递阶层次就形成了:
3.构造判断矩阵(成对比较阵)并赋值
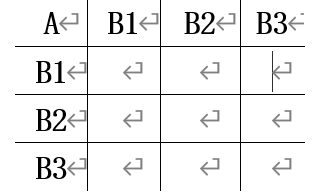
1、构造判断矩阵的方法:
每一个具有向下隶属关系的元素(被称作准则)作为判断矩阵的第一个元素(位于左上角),隶属于它的各个元素依次排列在其后的第一行和第一列。
如下图所示:
2、如何对判断矩阵进行赋值:
向填写人(专家)反复询问:针对判断矩阵的准则,其中两个元素两两比较哪个重要,重要多少,对重要性程度按1-9赋值。
(可以类比模糊PID中的隶属程度,都是人为设定的,也是被人诟病的一个地方)

设填写后的判断矩阵为A=(aij)n×n,判断矩阵具有如下性质:
(1) aij>0
(2) aji=1/ aji
(3) aii=1
判断矩阵具有对称性,因此在填写时,通常先填写aii=1部分,然后再仅需判断及填写上三角形或下三角形的n(n-1)/2个元素就可以了。
在特殊情况下,判断矩阵可以具有传递性,即满足等式:aij*ajk=aik .
当上式对判断矩阵所有元素都成立时,则称该判断矩阵为一致性矩阵。
对于上述的例子,可以构造出下面的判断矩阵:

4.层次单排序(计算权向量)与检验(一致性检验)
计算权向量
对于专家填写后的判断矩阵,利用一定数学方法进行层次排序。
层次单排序是指每一个判断矩阵各因素针对其准则的相对权重,所以本质上是计算权向量。
这里简要介绍和法:
对于一致性判断矩阵,每一列归一化后就是相应的权重。
对于非一致性判断矩阵,每一列归一化后近似其相应的权重,在对这n个列向量求取算术平均值作为最后的权重。
公式: 
在层层排序中,要对判断矩阵进行一致性检验。判断矩阵可以具有传递性和一致性。一般情况下,并不要求判断矩阵严格满足这一性质。
但从人类认识规律看,一个正确的判断矩阵重要性排序是有一定逻辑规律的,例如若A比B重要,B又比C重要,则从逻辑上讲,A应该比C明显重要,若两两比较时出现A比C重要的结果,则该判断矩阵违反了一致性准则,在逻辑上是不合理的。
因此在实际中要求判断矩阵满足大体上的一致性,需进行一致性检验。只有通过检验,才能说明判断矩阵在逻辑上是合理的,才能继续对结果进行分析。
一致性检验
第一步,计算一致性指标CI

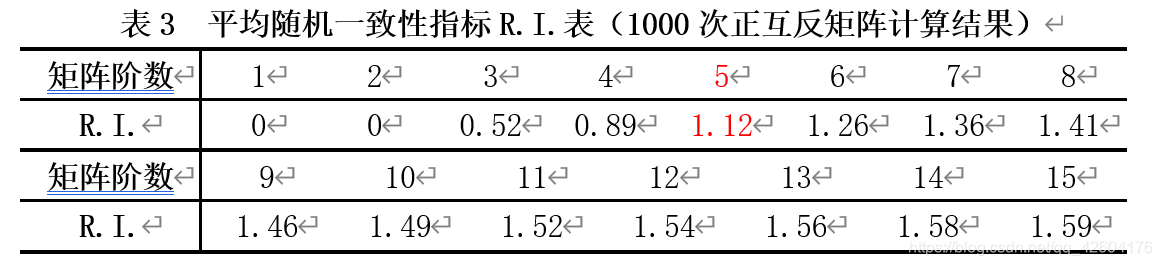
第二步,查表确定相应的平均随机一致性指标RI
据判断矩阵不同阶数查下表,得到平均随机一致性指标RI:
第三步,计算一致性比例CR并进行判断:
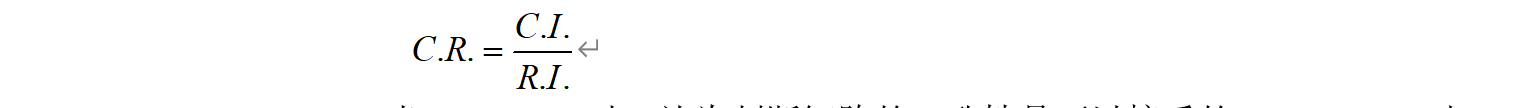
当C.R.<0.1时,认为判断矩阵的一致性是可以接受的,C.R.>0.1时,认为判断矩阵不符合一致性要求,需要对该判断矩阵进行重新修正。
 图1 图1 |  图2 图2 |
5.层次总排序(组合权向量)与检验(一致性检验)
总排序是指每一个判断矩阵各因素针对目标层(最上层)的相对权重。这一权重的计算采用从上而下的方法,逐层合成。
文字性描述公式如下:

计算过程如下,更好理解过程:
P(C1/A) = P(C1/B1) * P(B1/A) = 0.5 * 0.1429 = 0.07145
CR(C1/A) = CR(C/B) * CR(B/A) = 0 * 0 = 0
P(D1/A) = P(D1/C1) * P(C1/B1) * P(B1/A)
+ P(D1/C2) * P(C2/B1) * P(B1/A)
+ P(D1/C3) * P(C3/B2) * P(B2/A)
+ P(D1/C4) * P(C4/B2) * P(B2/A)
+ P(D1/C5) * P(C5/B3) * P(B3/A)
+ P(D1/C6) * P(C6/B3) * P(B3/A)
=0.8333 * 0.5 * 0.1429
+0.75 * 0.5 * 0.1429
+0.1667 * 0.75 * 0.4286
+0.8750 * 0.25 * 0.4286
+0.1667 * 0.75 * 0.4286
+0.8333 * 0.25 * 0.4286
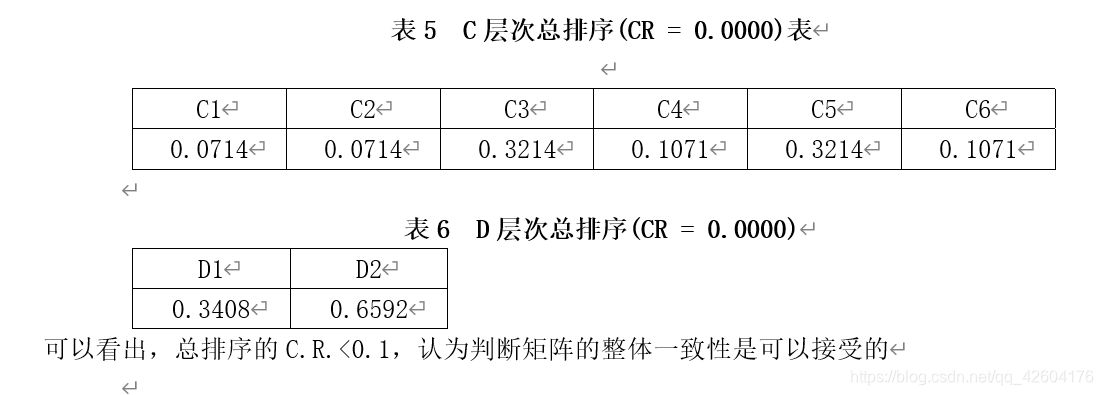
6.结果分析
从方案层总排序的结果看,建地铁(D2)的权重(0.6592)远远大于建高速路(D1)的权重(0.3408),因此,最终的决策方案是建地铁。
根据层次排序过程分析决策思路:
1、对于准则层B的3个因子,直接经济效益(B1)的权重最低(0.1429),社会效益(B2)和环境效益(B3)的权重都比较高(皆为0.4286),说明在决策中比较看重社会效益和环境效益。
2、对于不看重的经济效益,其影响的两个因子直接经济效益(C1)、间接带动效益(C2)单排序权重都是建高速路远远大于建地铁,对于比较看重的社会效益和环境效益,其影响的四个因子中有三个因子的单排序权重都是建地铁远远大于建高速路,由此可以推出,建地铁方案由于社会效益和环境效益较为突出,权重也会相对突出。
3、从准则层C总排序结果也可以看出,方便日常出行(C3)、减少环境污染(C5)是权重值较大的,而如果单独考虑这两个因素,方案排序都是建地铁远远大于建高速路。
由此我们可以分析出决策思路:
即决策比较看重的是社会效益和环境效益,不太看重经济效益;(总结准则层B)
因此对于具体因子,方便日常出行和减少环境污染成为主要考虑因素,对于这两个因素,都是建地铁方案更佳,(总结准则层C)由此,最终的方案选择建地铁也就顺理成章了。
7.层次分析法的优缺点
优点:
(1)系统性:层次分析把研究对象作为一个系统,按照分解、比较判断、综合的思维方式进行决策,成为继机理分析、统计分析之后发展起来的系统分析的重要工具。
(2)实用性:层次分析把定性和定量方法结合起来,能处理许多许多用传统的最优化技术无法着手的实际问题,应用范围很广。同时,这种方法将决策者和决策分析者相互沟通,决策者甚至可以直接应用它,这就增加了决策者的了解和掌握。
(3)简洁性:具有中等文化程度的人即可了解层次分析的基本原理和掌握它的基本步骤,计算也非常简便,并且所得的结果简单明确,容易为决策者了解和掌握。
缺点:囿旧:只能从原有方案中选优,不能生成新方案;粗略:它的比较、判断直到结果都是粗糙的,不适于精度要求很高的问题;主观:从建立层次结构模型到给出成对比较矩阵,人的主观因素的作用很大,这就使得决策结果可能难以为众人接受。当然,采取专家群体判断的办法是克服这个缺点的一种途径。
层次分析法的代码实现(matlab)
disp('请输入判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A);
x=ones(n,100);
y=ones(n,100);
m=zeros(1,100);
m(1)=max(x(:,1));
y(:,1)=x(:,1);
x(:,2)=A*y(:,1);
m(2)=max(x(:,2));
y(:,2)=x(:,2)/m(2);
p=0.0001;i=2;k=abs(m(2)-m(1));
while k>pi=i+1;x(:,i)=A*y(:,i-1);m(i)=max(x(:,i));y(:,i)=x(:,i)/m(i);k=abs(m(i)-m(i-1));
end
a=sum(y(:,i));
w=y(:,i)/a;
t=m(i);
disp(w);disp(t);%以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
if CR<0.10disp('此矩阵的一致性可以接受!');disp('CI=');disp(CI);disp('CR=');disp(CR);
end
使用示例:
将上面代码保存名为test1,并在点运行的时候添加到路径;
输入的A矩阵是要以向量的形式输入的;
之后按下回车即可,可以看到和之前的第4步得到的结果是一样的。

通过不断的使用这个式子计算相应矩阵(准则层B到准则层C、准则层C到方案层D)的权向量,最后可以得到最终的结果。
简单的修改上面的程序,传入参数为矩阵,免得每次都要打。
function w= test1(A)
% disp('请输入判断矩阵A(n阶)');
% A=input('A=');
[n,n]=size(A);
x=ones(n,100);
y=ones(n,100);
m=zeros(1,100);
m(1)=max(x(:,1));
y(:,1)=x(:,1);
x(:,2)=A*y(:,1);
m(2)=max(x(:,2));
y(:,2)=x(:,2)/m(2);
p=0.0001;i=2;k=abs(m(2)-m(1));
while k>pi=i+1;x(:,i)=A*y(:,i-1);m(i)=max(x(:,i));y(:,i)=x(:,i)/m(i);k=abs(m(i)-m(i-1));
end
a=sum(y(:,i));
w=y(:,i)/a;
t=m(i);
disp(w);disp(t);%以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
if CR<0.10disp('此矩阵的一致性可以接受!');disp('CI=');disp(CI);disp('CR=');disp(CR);
end
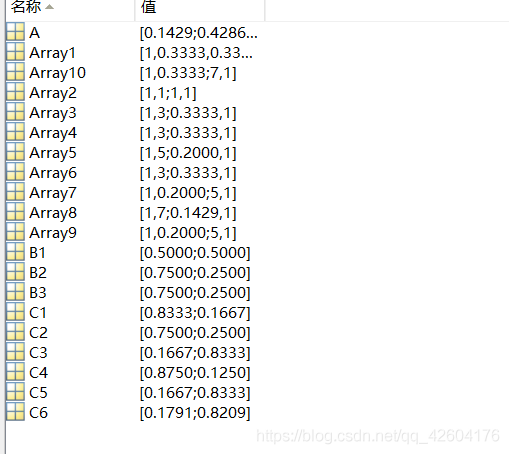
输入:
Array1=[1 1/3 1/3;3 1 1;3 1 1];
Array2=[1 1;1 1];
Array3=[1 3;1/3 1];
Array4=[1 3;1/3 1];
Array5=[1 5;1/5 1];
Array6=[1 3;1/3 1];
Array7=[1 1/5;5 1];
Array8=[1 7;1/7 1];
Array9=[1 1/5;5 1];
Array10=[1 1/3;7 1];A=test1(Array1);
B1=test1(Array2);
B2=test1(Array3);
B3=test1(Array4);
C1=test1(Array5);
C2=test1(Array6);
C3=test1(Array7);
C4=test1(Array8);
C5=test1(Array9);
C6=test1(Array10);
得到相应的矩阵:


)











)




