目录

• • 题目
  • 贪心法

题目

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例1：

输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例2：

输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例3：

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

贪心法

一看到这个题目，联想到之前做的另外一道题目：leetcode 376. 摆动序列 思考分析
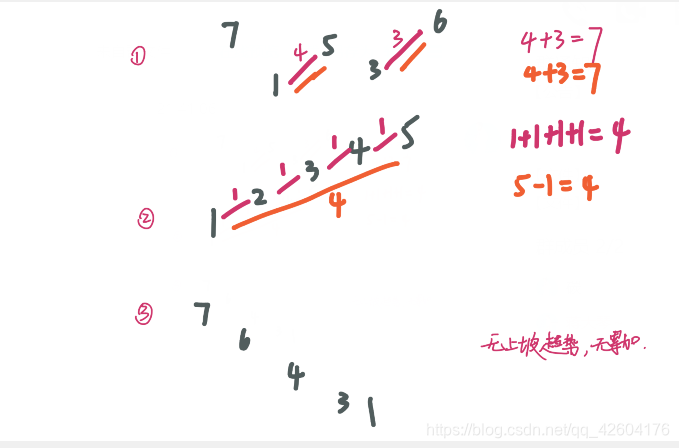
然后试着将三个示例画出波动图：
发现答案都符合一个特征：
结果 = 每个上坡阶段的坡顶与坡底的差值之和，也就是图中橘色部分表示。后来感觉这个写比较麻烦，于是想到简化一下，也就是品红色的方法。
可以发现，对于每个上坡，坡顶与坡底的差值等于上坡阶段中每一个子差之和。

这样代码就好写很多了：

class Solution {
public:int maxProfit(vector<int>& prices) {int up_ramp_sum = 0;for(int i = 1;i < prices.size();i++){if(prices[i] > prices[i-1]){up_ramp_sum+=(prices[i] - prices[i-1]);}}return up_ramp_sum;}
};

//TODO
之后复习到动态规划再写动态规划的方法。