1、移动平均

moving average方法

moving average方法不适合我们进行长期的预测（为了预测下一个值，我们需要实际观察的上一个值）。但是 移动平均数 还有另一个应用场景，即对原始的时间序列数据进行平滑处理，以找到数据的变化趋势。
pandas 提供了一个实现接口 DataFrame.rolling(window).mean() ，滑动窗口 window 的值越大，意味着变化趋势将会越平滑，对于那些噪音点很多的数据集（尤其是金融数据），使用 pandas 的这个接口，有助于探测到数据中存在的共性（common pattern）
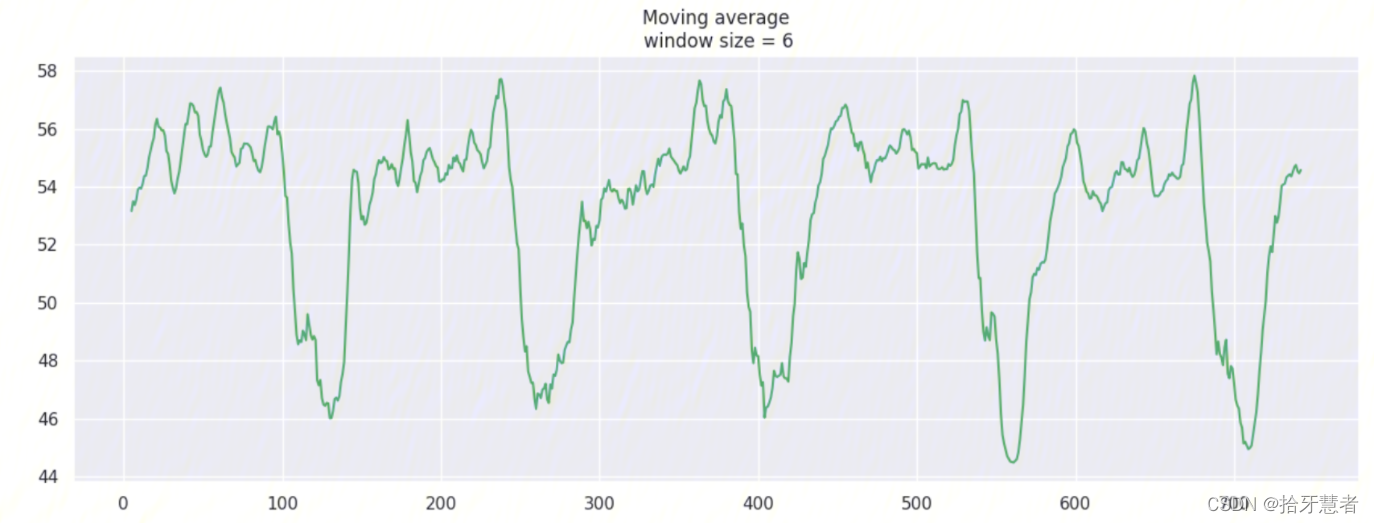
由于数据采集gap为10min，接下来我们调整window大小，看看分别有什么效果。
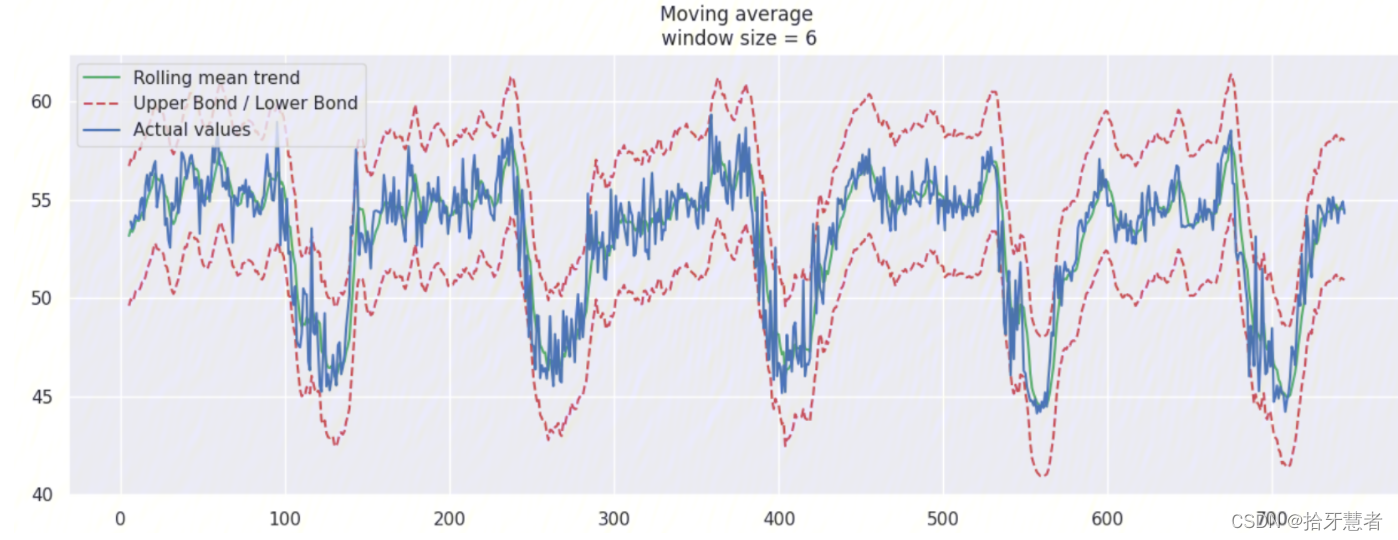
window_size = 6 -> 1h:

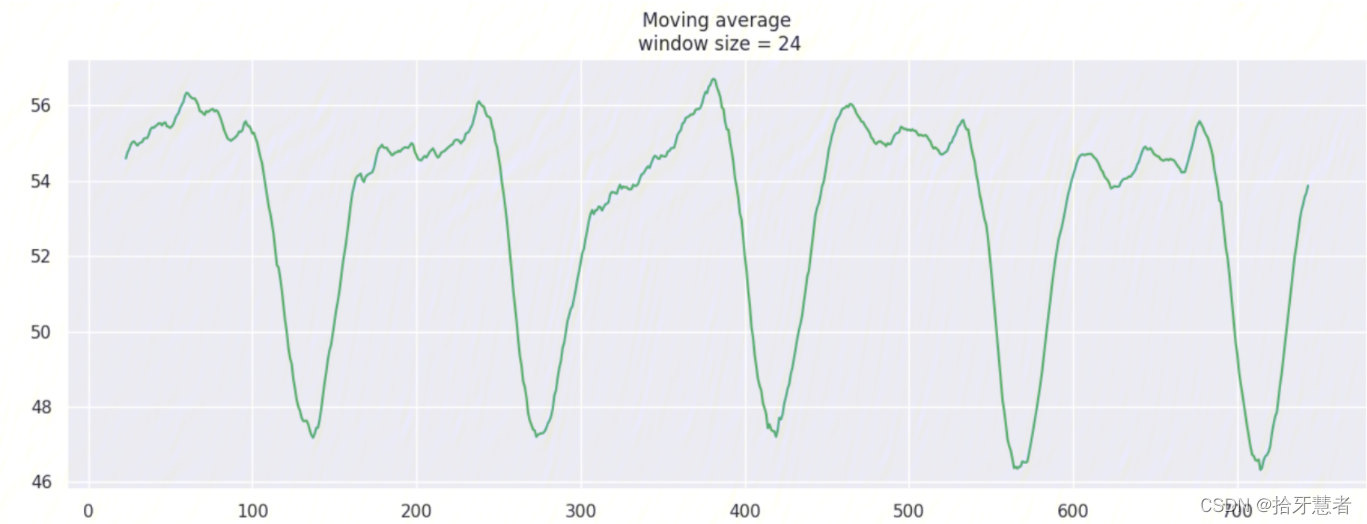
window_size = 24 -> 4h:

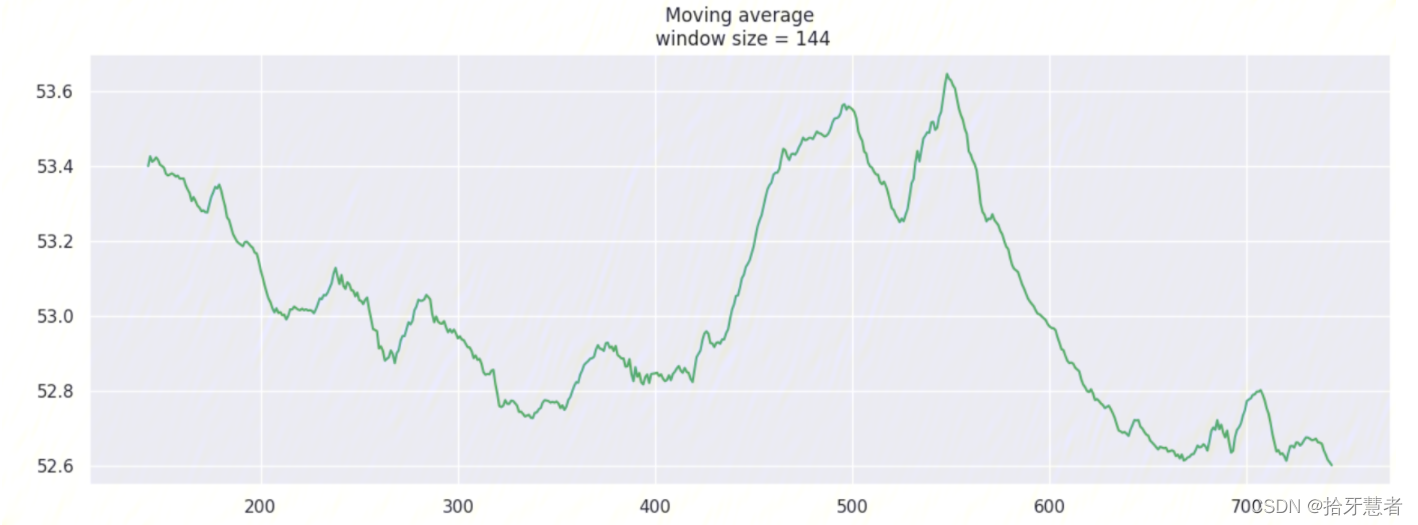
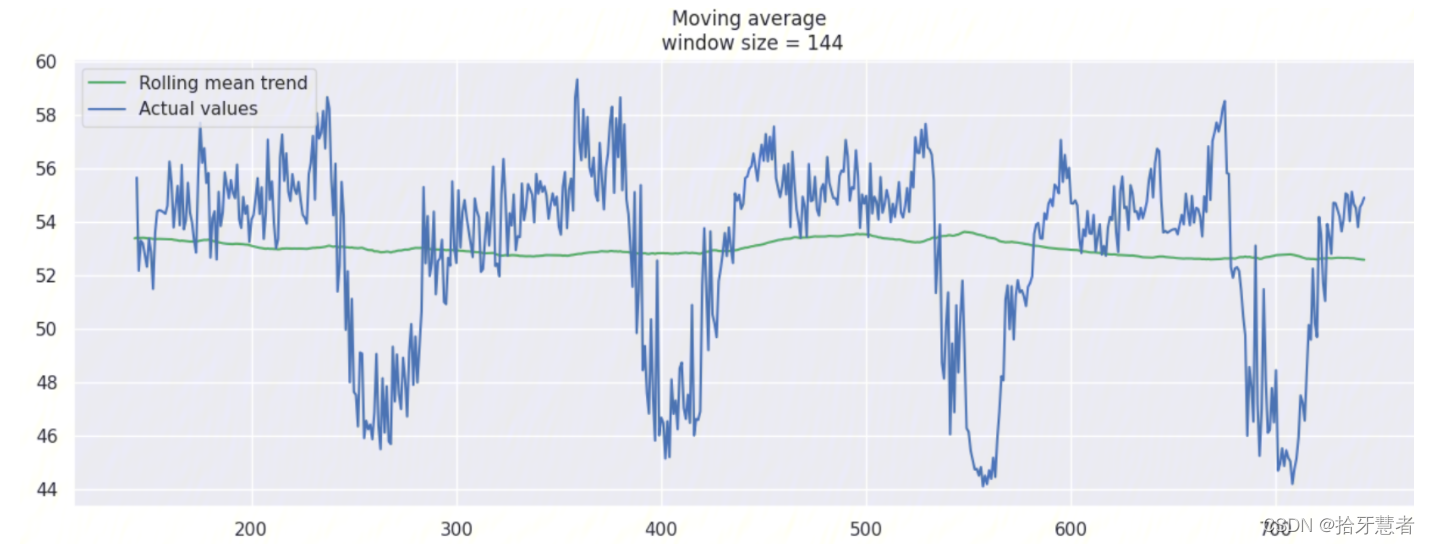
window_size = 144 -> 24h:

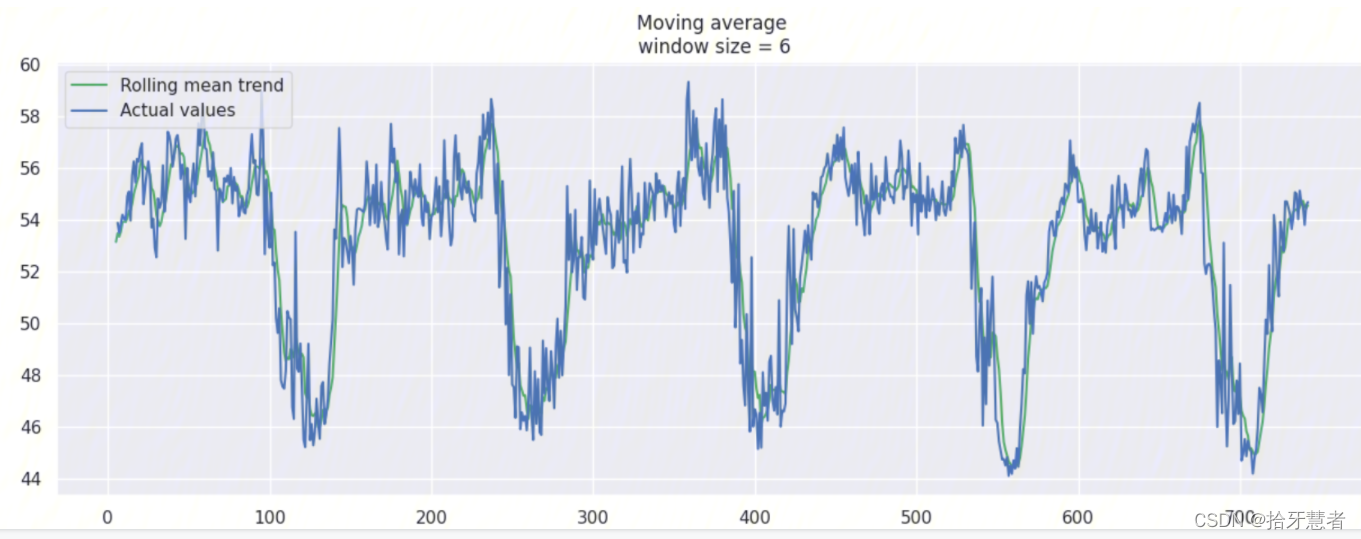
这里我们针对window_size = 6加上置信区间（scale=1.96）

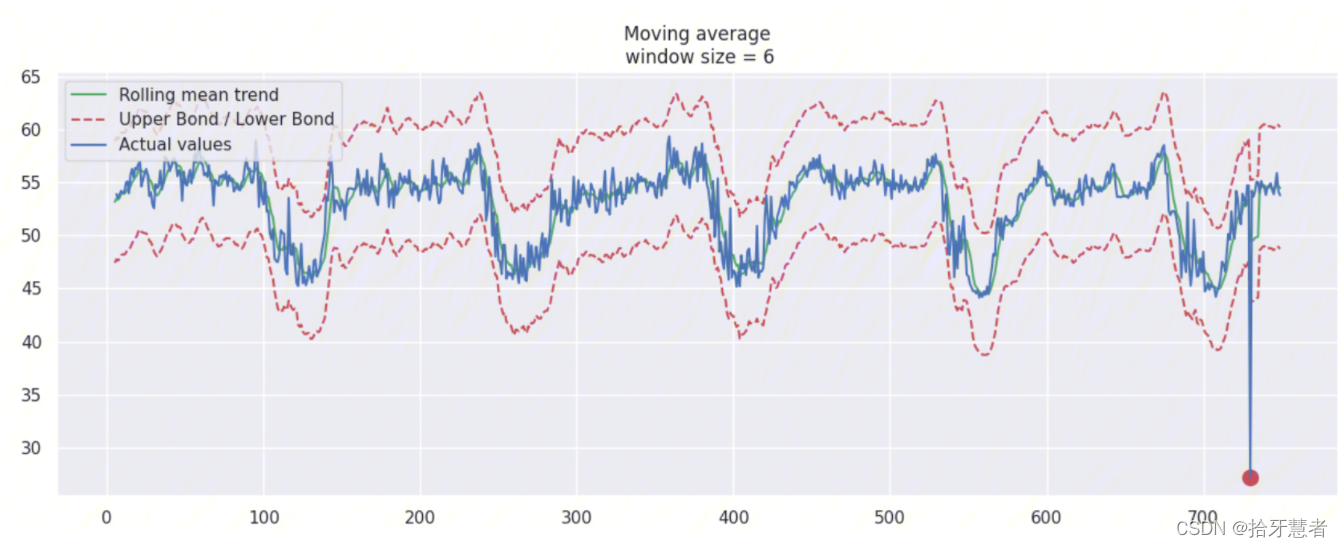
我们可以基于 moving average 创建一个简单的异常检测系统（即如果数据点在置信区间之外，则认为是异常值）
这里我们进行数据造假+扩大置信区间（scale=2.96）：

rtt_anomaly = df.rtt.copy()
rtt_anomaly.iloc[-20] = rtt_anomaly.iloc[-20] * 0.5 # say we have 80% drop of ads

weighted average方法

上面提到了用 移动平均值对原始数据做平滑处理，接下来要说的是加权平均值，它是对上面 移动平均值 的简单改良。
也就是说，前面 k 个观测数据的值，不再是直接求和再取平均值，而是计算它们的加权和（权重和为1）。通常来说，时间距离越近的观测点，权重越大。数学表达式为：

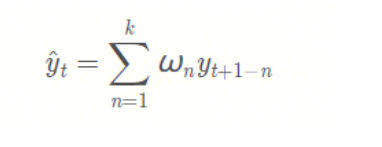
def weighted_average(series, weights):"""Calculate weighter average on series"""result = 0.0weights.reverse()for n in range(len(weights)):result += series.iloc[-n-1] * weights[n]return float(result)weighted_average(ads, [0.6, 0.3, 0.1])

2、指数平滑

单指数平滑 exponential_smoothing

如果不用上面提到的， /每次对当前序列中的前k个数/ 的加权平均值作为模型的预测值，而是直接对 /目前所有的已观测数据/ 进行加权处理，并且每一个数据点的权重，呈指数形式递减。
  这个就是指数平滑的策略，具体怎么做的呢？一个简单的数学式为：

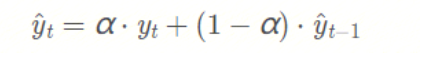
式子中的 α \alphaα 表示平滑因子，它定义我们“遗忘”当前真实观测值的速度有多快。α \alphaα 越小，表示当前真实观测值的影响力越小，而前一个模型预测值的影响力越大，最终得到的时间序列将会越平滑。
下面是选择不同的权重得到的曲线：

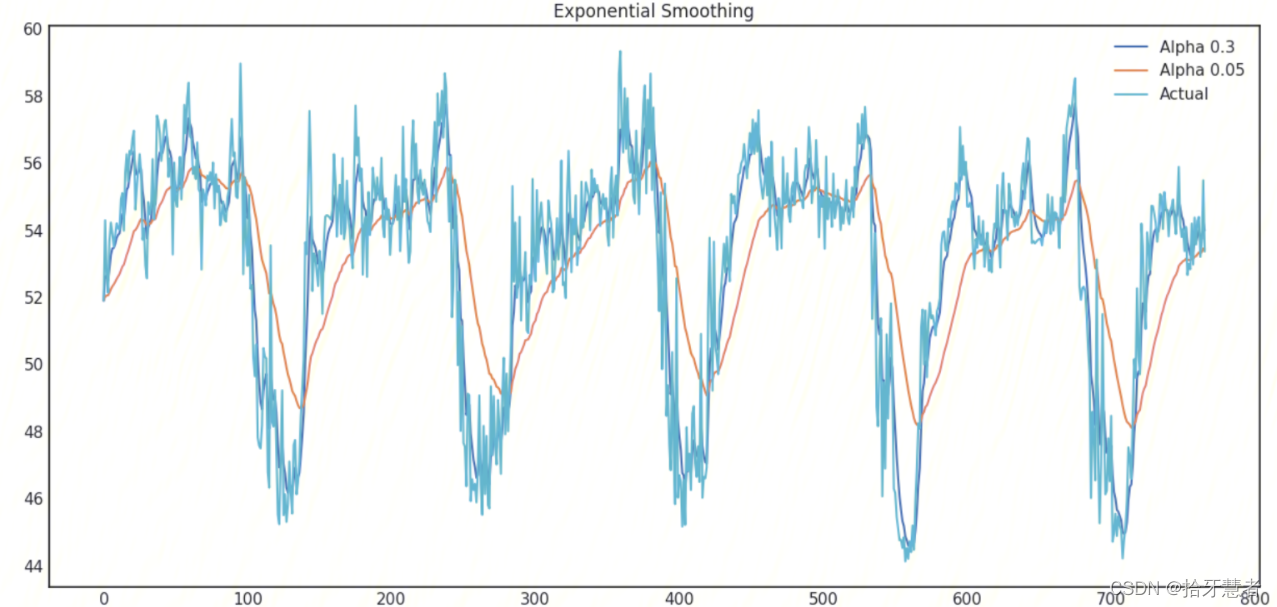
1. 单指数平滑的特点： 能够追踪数据变化。预测过程中，添加了最新的样本数据之后，新数据逐渐取代老数据的地位，最终老数据被淘汰。
2. 单指数平滑的局限性： 第一，预测值不能反映趋势变动、季节波动等有规律的变动；第二，这个方法多适用于短期预测，而不适合中长期的预测；第三，由于预测值是历史数据的均值，因此与实际序列相比，有滞后的现象。
3. 单指数平滑的系数： EViews提供两种确定指数平滑系数的方法：自动给定和人工确定。一般来说，如果序列变化比较平缓，平滑系数值应该比较小，比如小于0.l；如果序列变化比较剧烈，平滑系数值可以取得大一些，如0.3～0.5。若平滑系数值大于0.5才能跟上序列的变化，表明序列有很强的趋势，不能采用一次指数平滑进行预测。

双指数平滑

单指数平滑在产生新的序列的时候，考虑了前面的 K 条历史数据，但是仅仅考虑其静态值，即没有考虑时间序列当前的变化趋势。
  如果当前的时间序列数据处于上升趋势，那么当我们对明天的数据进行预测的时候，就不应该仅仅是对历史数据进行”平均“，还应考虑到当前数据变化的上升趋势。同时考虑历史平均和变化趋势，这个就是我们的双指数平滑法。
通过 序列分解法 (series decomposition)，我们可以得到两个分量，一个叫 intercept (also, level) ℓ \ellℓ ，另一个叫 trend (also, slope，斜率) b bb. 我们根据前面学习的方法，知道了如何预测 intercept （截距，即序列数据的期望值），我们可以将同样的指数平滑法应用到 trend (趋势)上。时间序列未来变化的方向取决于先前加权的变化。

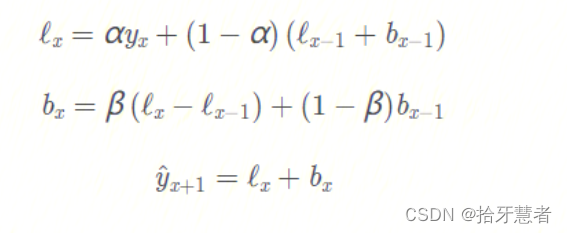
在不同平滑因子的组合下的时序图:

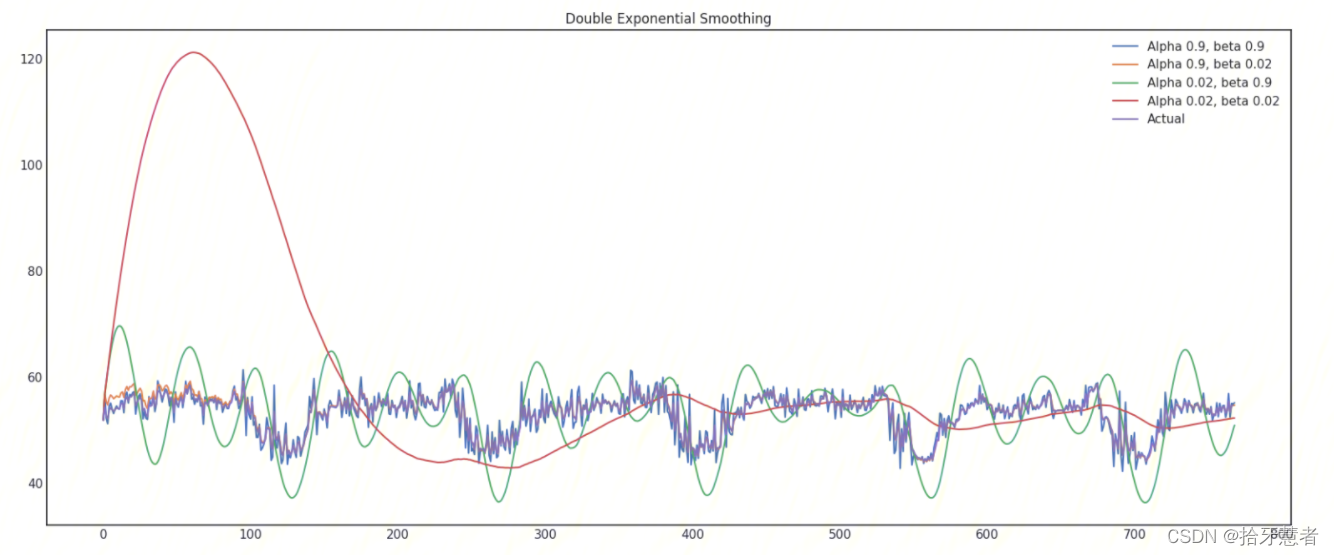
调整两个参数 α \alphaα 和 β \betaβ 。前者决定时间序列数据自身变化趋势的平滑程度，后者决定趋势的平滑程度

三指数平滑 Triple exponential smoothing

三指数平滑，也叫 Holt-Winters 平滑，与前两种平滑方法相比，我们这次多考虑了一个因素，seasonality （季节性）。这其实也意味着，如果我们的时间序列数据，不存在季节性变化，就不适合用三指数平滑。
  模型中的 季节性 分量，用来解释 截距 和 趋势 的重复变化，并且由季节长度来描述，也就是变化重复的周期来描述。
  对于一个周期内的每一个观测点，都有一个单独的组成部分。

我们根据常识可知，这个数据集中，存在一个明显的季节性变化，变化周期为24小时，因此我们设置 slen = 24*6 = 144 :
在 Holt-Winters 模型以及其他指数平滑模型中，对平滑参数的大小有一个限制，每个参数都在0到1之间。因此我们必须选择支持模型参数约束的最优化算法，在这里，我们使用 Truncated Newton conjugate gradient (截断牛顿共轭梯度法)

3、平稳性以及时间序列建模

在我们开始建模之前，我们需要提到时间序列的一个重要特性，如平稳性 (stationarity)。
  我们称一个时间序列是平稳的，是指它不会随时间而改变其统计特性，即平均值和方差不会随时间而改变。
因为现在大多数的时间序列模型，或多或少都是基于未来序列与目前已观测到的序列数据有着相同的统计特性(均值、方差等) 的假设。也就是说，如果原始序列（已观测序列）是不平稳的，那么我们现有模型的预测结果，就可能会出错。
  糟糕的是，我们在教科书之外所接触到的时间序列数据，大多都是不平稳的，不过还好，我们有办法把它改变成平稳分布。
如果我们可以用一阶差分从非平稳序列中得到一个平稳序列，我们称这个非平稳序列为一阶积分。我们可以使用不同的方法来对抗非平稳性，如 d阶差分、趋势和季节性消除、平滑处理，也可以使用像box cox或对数这样的转换。

SARIMA模型

1、绘制时间序列图、ACF 图和 PACF 图

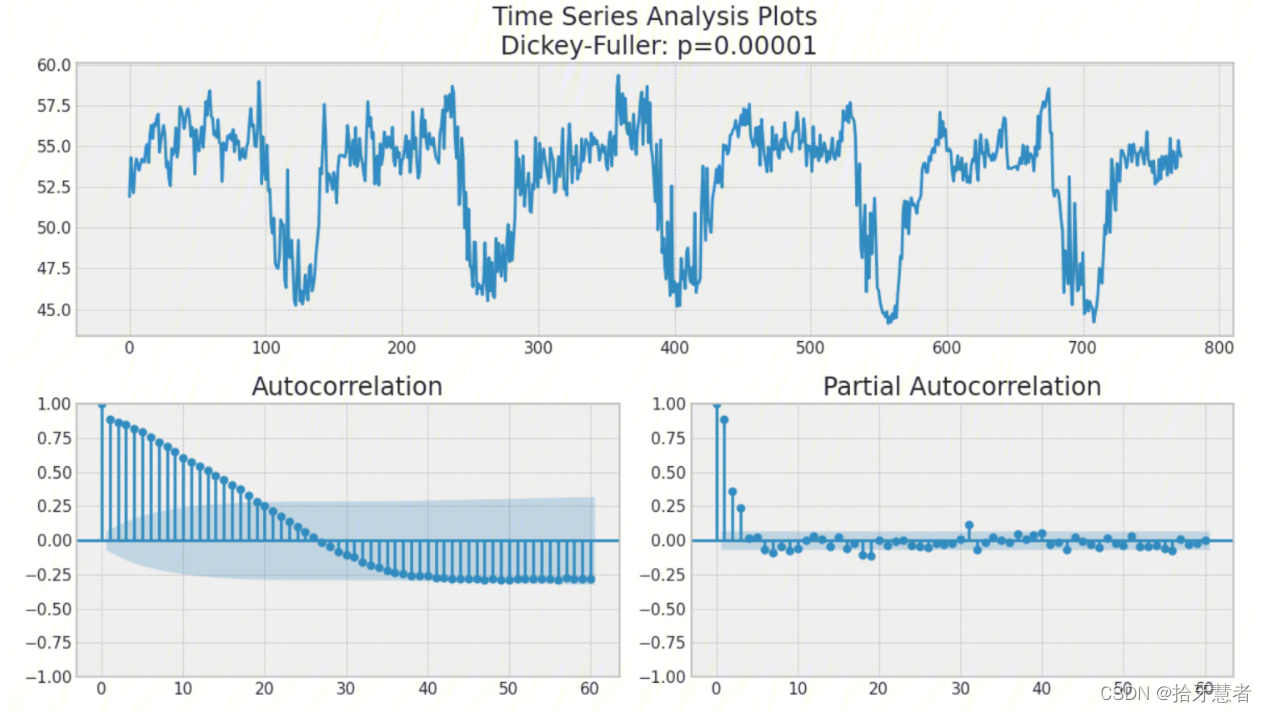
Autocorrelation Function (ACF)自相关函数，指任意时间 t（t=1,2,3…n)的 序列值X^^t^ 与其自身的滞后（这里取滞后一阶，即lag=1）值X^^t-1^之间的线性关系。
这个图看不太懂，先试试其他的方法

4、时间序列的（非）线性模型

时间序列的滞后值

将时间序列来回移动 n 步，我们能得到一个特征，其中时序的当前值和其t-n时刻的值对齐。如果我们移动1时差，并训练模型预测未来，那么模型将能够提前预测1步。增加时差，比如，增加到6，可以让模型提前预测6步，不过它需要在观测到数据的6步之后才能利用。

使用线性回归

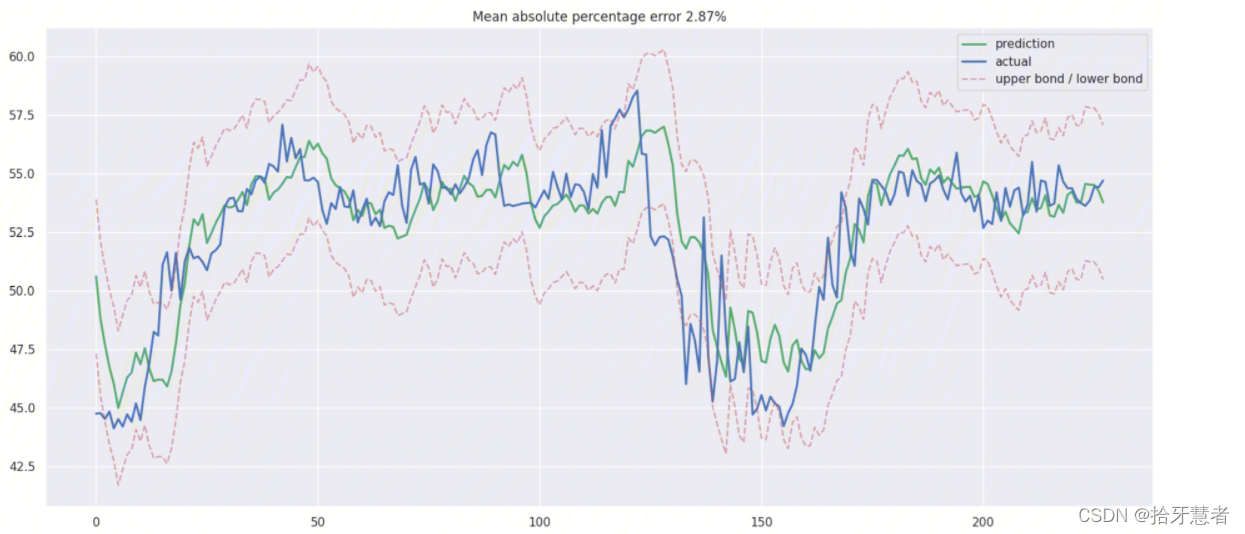
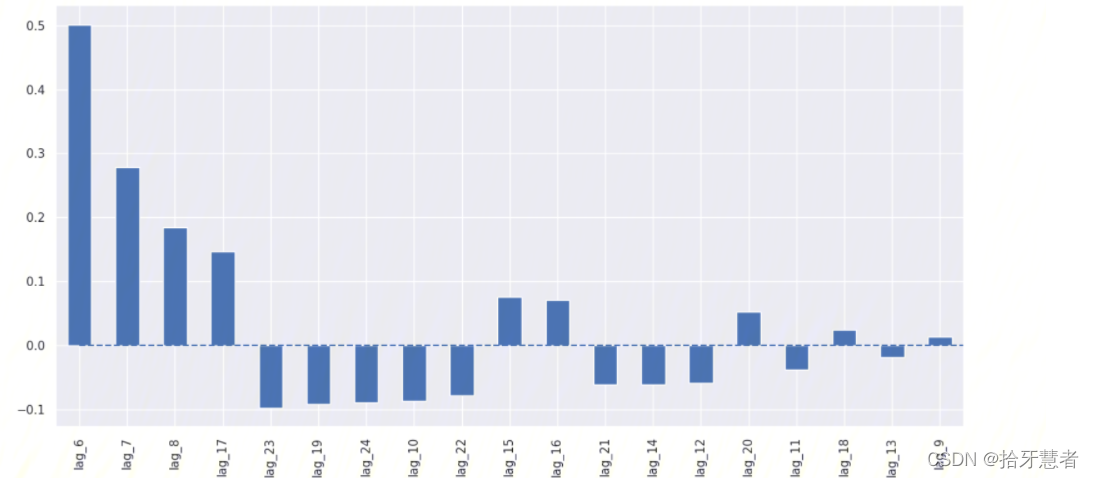
里面有大量不必要的特征。

XGBoost

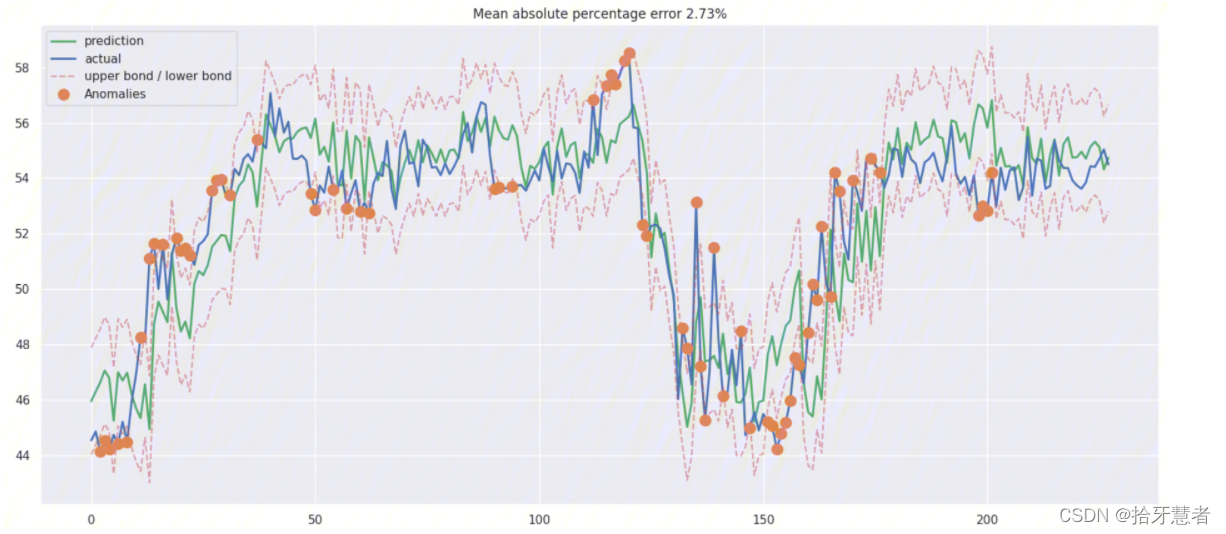
5、一些疑惑以及技术选型

1、时间序列的（非）线性模型中将时间序列来回移动获取的特征的意义还不太懂，感觉是几阶差分。但是从拟合结果来看感觉还可以。还需要更细致的研究一下。但是无论是线性回归还是随机森林得到的pred，时间序列开始的部分匹配率都很差，得研究一下为什么。
2、SARIMA模型的ACF 图和 PACF 图看不懂，并且在工作中，构建模型的原则是快、好、省。 这也就意味着有些模型并不适合用于生产环境。因为它们需要过长的数据准备时间，或者需要频繁地重新训练新数据，或者很难调整参数（SARIMA 模型就包含了着三个缺点）。
3、双指数平滑、三指数平滑调参比较复杂，不过也有一定实现意义
4、moving average简单，不过容易把一些周期性的峰值判断成异常数据，这是因为它没有在我们的数据中捕捉到周期中出现的季节性变化。
5、划分数据集和训练集的代码还得再看看。
6、当数据库中数据被填满的时候（也就是7天的数据量：7 x 24 x 6 = 1,008），每插入一条新数据，最旧的一条数据就被会抛弃掉。所以序列整体就是会平移。这样的话使用旧模型就会有问题了，可以通过编程手段，拟合出一周的模型：周一0点->周日24点的模型。然后每次获取db数据的时候进行剪裁，换算出当前数据在本周的位置。
7、考虑对哪些维度的数据进行模型拟合。

6、文章参考

【Python】时间序列分析完整过程：https://blog.csdn.net/jh1137921986/article/details/90257764
时间序列与时间序列分析：https://www.cnblogs.com/tianqizhi/p/9277376.html
如何根据自相关（ACF）图和偏自相关（PACF）图选择ARIMA模型的p、q值：https://blog.csdn.net/weixin_41013322/article/details/108801516

7、代码附录

前两个py文件放在/var/www/html/NewTest/InternShipProject/my_pylib目录下作为库文件，所以细节代码就在这里面了。

传统模型法

my_time_series_algorithm.py

import numpy as np                               # 向量和矩阵运算
import pandas as pd                              # 表格与数据处理
import matplotlib.pyplot as plt                  # 绘图
import seaborn as sns                            # 更多绘图功能
sns.set()from dateutil.relativedelta import relativedelta # 日期数据处理
from scipy.optimize import minimize              # 优化函数import statsmodels.formula.api as smf            # 数理统计
import statsmodels.tsa.api as smt
import statsmodels.api as sm
import scipy.stats as scsfrom itertools import product                    # 一些有用的函数
from tqdm import tqdm_notebookimport warnings                                  # 勿扰模式
warnings.filterwarnings('ignore')from sklearn.metrics import r2_score, median_absolute_error, mean_absolute_error
from sklearn.metrics import median_absolute_error, mean_squared_error, mean_squared_log_error
from sklearn.model_selection import TimeSeriesSplit # you have everything done for youdef mean_absolute_percentage_error(y_true, y_pred): return np.mean(np.abs((y_true - y_pred) / y_true)) * 100# 加权平均
def weighted_average(series, weights):"""Calculate weighter average on series"""result = 0.0weights.reverse()for n in range(len(weights)):result += series.iloc[-n-1] * weights[n]return float(result)def move_average(series, window):return series.rolling(window=window).mean()# 滑动平均 
def plotMovingAverage(series, window, plot_intervals=False, scale=2.96, plot_anomalies=False, pic_name="plotMovingAverage"):"""series - dataframe with timeserieswindow - rolling window size plot_intervals - show confidence intervalsplot_anomalies - show anomalies """rolling_mean = move_average(series, window)plt.figure(figsize=(15,5))plt.title("Moving average\n window size = {}".format(window))plt.plot(rolling_mean, "g", label="Rolling mean trend")plt.savefig('/var/www/html/NewTest/pics/%s.png' % "rolling_mean")# Plot confidence intervals for smoothed valuesif plot_intervals:mae = mean_absolute_error(series[window:], rolling_mean[window:])deviation = np.std(series[window:] - rolling_mean[window:])lower_bond = rolling_mean - (mae + scale * deviation)upper_bond = rolling_mean + (mae + scale * deviation)plt.plot(upper_bond, "r--", label="Upper Bond / Lower Bond")plt.plot(lower_bond, "r--")# Having the intervals, find abnormal valuesif plot_anomalies:anomalies = series[window:].copy()print(anomalies)for i in series[window:].index:if (series[window:][i] >= lower_bond[i]) and (series[window:][i] <= upper_bond[i]):anomalies[i] = Noneprint(anomalies)plt.plot(anomalies, "ro", markersize=10)plt.plot(series[window:], label="Actual values")plt.legend(loc="upper left")plt.savefig('/var/www/html/NewTest/pics/%s.png' % pic_name)plt.grid(True)# 单指数平滑
def exponential_smoothing(series, alpha):"""series - dataset with timestampsalpha - float [0.0, 1.0], smoothing parameter"""result = [series[0]] # first value is same as seriesfor n in range(1, len(series)):result.append(alpha * series[n] + (1 - alpha) * result[n-1])return result# 绘制单指数平滑曲线    
def plotExponentialSmoothing(series, alphas, pic_name="plotExponentialSmoothing"):"""Plots exponential smoothing with different alphasseries - dataset with timestampsalphas - list of floats, smoothing parameters"""with plt.style.context('seaborn-white'):    plt.figure(figsize=(15, 7))for alpha in alphas:plt.plot(exponential_smoothing(series, alpha), label="Alpha {}".format(alpha))plt.plot(series.values, "c", label = "Actual")plt.legend(loc="best")plt.axis('tight')plt.title("Exponential Smoothing")plt.savefig('/var/www/html/NewTest/pics/%s.png' % pic_name)plt.grid(True);# 双指数平滑
def double_exponential_smoothing(series, alpha, beta):"""series - dataset with timeseriesalpha - float [0.0, 1.0], smoothing parameter for levelbeta - float [0.0, 1.0], smoothing parameter for trend"""# first value is same as seriesresult = [series[0]]for n in range(1, len(series)+1):if n == 1:level, trend = series[0], series[1] - series[0]if n >= len(series): # forecastingvalue = result[-1]else:value = series[n]last_level, level = level, alpha*value + (1-alpha)*(level+trend)trend = beta*(level-last_level) + (1-beta)*trendresult.append(level+trend)return result# 绘制双指数平滑曲线 
def plotDoubleExponentialSmoothing(series, alphas, betas, pic_name="plotExponentialSmoothing"):"""Plots double exponential smoothing with different alphas and betasseries - dataset with timestampsalphas - list of floats, smoothing parameters for levelbetas - list of floats, smoothing parameters for trend"""with plt.style.context('seaborn-white'):    plt.figure(figsize=(20, 8))for alpha in alphas:for beta in betas:plt.plot(double_exponential_smoothing(series, alpha, beta), label="Alpha {}, beta {}".format(alpha, beta))plt.plot(series.values, label = "Actual")plt.legend(loc="best")plt.axis('tight')plt.title("Double Exponential Smoothing")plt.savefig('/var/www/html/NewTest/pics/%s.png' % pic_name)plt.grid(True)# Holt-Winters model
class HoltWinters:"""Holt-Winters model with the anomalies detection using Brutlag method# series - initial time series# slen - length of a season# alpha, beta, gamma - Holt-Winters model coefficients# n_preds - predictions horizon# scaling_factor - sets the width of the confidence interval by Brutlag (usually takes values from 2 to 3)"""def __init__(self, series, slen, alpha, beta, gamma, n_preds, scaling_factor=1.96):self.series = seriesself.slen = slenself.alpha = alphaself.beta = betaself.gamma = gammaself.n_preds = n_predsself.scaling_factor = scaling_factordef initial_trend(self):sum = 0.0for i in range(self.slen):sum += float(self.series[i+self.slen] - self.series[i]) / self.slenreturn sum / self.slen  def initial_seasonal_components(self):seasonals = {}season_averages = []n_seasons = int(len(self.series)/self.slen)# let's calculate season averagesfor j in range(n_seasons):season_averages.append(sum(self.series[self.slen*j:self.slen*j+self.slen])/float(self.slen))# let's calculate initial valuesfor i in range(self.slen):sum_of_vals_over_avg = 0.0for j in range(n_seasons):sum_of_vals_over_avg += self.series[self.slen*j+i]-season_averages[j]seasonals[i] = sum_of_vals_over_avg/n_seasonsreturn seasonals   def triple_exponential_smoothing(self):self.result = []self.Smooth = []self.Season = []self.Trend = []self.PredictedDeviation = []self.UpperBond = []self.LowerBond = []seasonals = self.initial_seasonal_components()for i in range(len(self.series)+self.n_preds):if i == 0: # components initializationsmooth = self.series[0]trend = self.initial_trend()self.result.append(self.series[0])self.Smooth.append(smooth)self.Trend.append(trend)self.Season.append(seasonals[i%self.slen])self.PredictedDeviation.append(0)self.UpperBond.append(self.result[0] + self.scaling_factor * self.PredictedDeviation[0])self.LowerBond.append(self.result[0] - self.scaling_factor * self.PredictedDeviation[0])continueif i >= len(self.series): # predictingm = i - len(self.series) + 1self.result.append((smooth + m*trend) + seasonals[i%self.slen])# when predicting we increase uncertainty on each stepself.PredictedDeviation.append(self.PredictedDeviation[-1]*1.01) else:val = self.series[i]last_smooth, smooth = smooth, self.alpha*(val-seasonals[i%self.slen]) + (1-self.alpha)*(smooth+trend)trend = self.beta * (smooth-last_smooth) + (1-self.beta)*trendseasonals[i%self.slen] = self.gamma*(val-smooth) + (1-self.gamma)*seasonals[i%self.slen]self.result.append(smooth+trend+seasonals[i%self.slen])# Deviation is calculated according to Brutlag algorithm.self.PredictedDeviation.append(self.gamma * np.abs(self.series[i] - self.result[i]) + (1-self.gamma)*self.PredictedDeviation[-1])self.UpperBond.append(self.result[-1] + self.scaling_factor * self.PredictedDeviation[-1])self.LowerBond.append(self.result[-1] - self.scaling_factor * self.PredictedDeviation[-1])self.Smooth.append(smooth)self.Trend.append(trend)self.Season.append(seasonals[i%self.slen])# 用于参数搜索
def timeseriesCVscore(params, series, loss_function=mean_squared_error, slen=144):"""Returns error on CV  params - vector of parameters for optimizationseries - dataset with timeseriesslen - season length for Holt-Winters model"""# errors arrayerrors = []values = series.valuesalpha, beta, gamma = params# set the number of folds for cross-validationtscv = TimeSeriesSplit(n_splits=3) # iterating over folds, train model on each, forecast and calculate errorfor train, test in tscv.split(values):model = HoltWinters(series=values[train], slen=slen, alpha=alpha, beta=beta, gamma=gamma, n_preds=len(test))model.triple_exponential_smoothing()predictions = model.result[-len(test):]actual = values[test]error = loss_function(predictions, actual)errors.append(error)return np.mean(np.array(errors))# 绘制三指数平滑曲线
def plotHoltWinters(series, model, plot_intervals=False, plot_anomalies=False):"""series - dataset with timeseriesplot_intervals - show confidence intervalsplot_anomalies - show anomalies """plt.figure(figsize=(20, 10))plt.plot(model.result, label = "Model")plt.plot(series.values, label = "Actual")error = mean_absolute_percentage_error(series.values, model.result[:len(series)])plt.title("Mean Absolute Percentage Error: {0:.2f}%".format(error))if plot_anomalies:anomalies = np.array([np.NaN]*len(series))anomalies[series.values<model.LowerBond[:len(series)]] = \series.values[series.values<model.LowerBond[:len(series)]]anomalies[series.values>model.UpperBond[:len(series)]] = \series.values[series.values>model.UpperBond[:len(series)]]plt.plot(anomalies, "o", markersize=10, label = "Anomalies")if plot_intervals:plt.plot(model.UpperBond, "r--", alpha=0.5, label = "Up/Low confidence")plt.plot(model.LowerBond, "r--", alpha=0.5)plt.fill_between(x=range(0,len(model.result)), y1=model.UpperBond, y2=model.LowerBond, alpha=0.2, color = "grey")    plt.vlines(len(series), ymin=min(model.LowerBond), ymax=max(model.UpperBond), linestyles='dashed')plt.axvspan(len(series)-20, len(model.result), alpha=0.3, color='lightgrey')plt.grid(True)plt.axis('tight')plt.legend(loc="best", fontsize=13);plt.savefig('/var/www/html/NewTest/pics/%s.png' % "plotHoltWinters")# 绘制时间序列图、ACF 图和 PACF 图
def tsplot(y, lags=None, figsize=(12, 7), style='bmh'):"""Plot time series, its ACF and PACF, calculate Dickey–Fuller testy - timeserieslags - how many lags to include in ACF, PACF calculation"""if not isinstance(y, pd.Series):y = pd.Series(y)with plt.style.context(style):    fig = plt.figure(figsize=figsize)layout = (2, 2)ts_ax = plt.subplot2grid(layout, (0, 0), colspan=2)acf_ax = plt.subplot2grid(layout, (1, 0))pacf_ax = plt.subplot2grid(layout, (1, 1))y.plot(ax=ts_ax)p_value = sm.tsa.stattools.adfuller(y)[1]ts_ax.set_title('Time Series Analysis Plots\n Dickey-Fuller: p={0:.5f}'.format(p_value))smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)plt.tight_layout()plt.savefig('/var/www/html/NewTest/pics/%s.png' % "tsplot")

机器学习的方法（线性回归、XGB）

my_machine_learning_algorithm.py

import numpy as np                               # 向量和矩阵运算
import pandas as pd                              # 表格与数据处理
import matplotlib.pyplot as plt                  # 绘图
import seaborn as sns                            # 更多绘图功能
sns.set()from dateutil.relativedelta import relativedelta # 日期数据处理
from scipy.optimize import minimize              # 优化函数import statsmodels.formula.api as smf            # 数理统计
import statsmodels.tsa.api as smt
import statsmodels.api as sm
import scipy.stats as scsfrom itertools import product                    # 一些有用的函数
from tqdm import tqdm_notebookimport warnings                                  # 勿扰模式
warnings.filterwarnings('ignore')from sklearn.metrics import r2_score, median_absolute_error, mean_absolute_error
from sklearn.metrics import median_absolute_error, mean_squared_error, mean_squared_log_error
from sklearn.model_selection import TimeSeriesSplit # you have everything done for youfrom sklearn.preprocessing import StandardScaler
scaler = StandardScaler()from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_scorefrom xgboost import XGBRegressor def mean_absolute_percentage_error(y_true, y_pred): return np.mean(np.abs((y_true - y_pred) / y_true)) * 100def timeseries_train_test_split(X, y, test_size):"""Perform train-test split with respect to time series structure"""# get the index after which test set startstest_index = int(len(X)*(1-test_size))X_train = X.iloc[:test_index]y_train = y.iloc[:test_index]X_test = X.iloc[test_index:]y_test = y.iloc[test_index:]return X_train, X_test, y_train, y_testdef plotModelResults(model, X_train, X_test, y_test, y_train, tscv, plot_intervals=False, plot_anomalies=False, scale=1.96, pic_name="plotModelResults"):"""Plots modelled vs fact values, prediction intervals and anomalies"""prediction = model.predict(X_test)plt.figure(figsize=(15, 7))plt.plot(prediction, "g", label="prediction", linewidth=2.0)plt.plot(y_test.values, label="actual", linewidth=2.0)if plot_intervals:cv = cross_val_score(model, X_train, y_train, cv=tscv, scoring="neg_mean_squared_error")#mae = cv.mean() * (-1)deviation = np.sqrt(cv.std())lower = prediction - (scale * deviation)upper = prediction + (scale * deviation)plt.plot(lower, "r--", label="upper bond / lower bond", alpha=0.5)plt.plot(upper, "r--", alpha=0.5)if plot_anomalies:anomalies = np.array([np.NaN]*len(y_test))anomalies[y_test<lower] = y_test[y_test<lower]anomalies[y_test>upper] = y_test[y_test>upper]plt.plot(anomalies, "o", markersize=10, label = "Anomalies")# print(prediction.flatten())# print(y_test)error = mean_absolute_percentage_error(prediction.flatten(), y_test)plt.title("Mean absolute percentage error {0:.2f}%".format(error))plt.legend(loc="best")plt.tight_layout()plt.grid(True);plt.savefig('/var/www/html/NewTest/pics/%s.png' % pic_name)def plotCoefficients(model, x_train, pic_name="plotCoefficients"):"""Plots sorted coefficient values of the model"""coefs = pd.DataFrame(model.coef_.flatten(), x_train.columns)coefs.columns = ["coef"]coefs["abs"] = coefs.coef.apply(np.abs)coefs = coefs.sort_values(by="abs", ascending=False).drop(["abs"], axis=1)plt.figure(figsize=(15, 7))coefs.coef.plot(kind='bar')plt.grid(True, axis='y')plt.hlines(y=0, xmin=0, xmax=len(coefs), linestyles='dashed');plt.savefig('/var/www/html/NewTest/pics/%s.png' % pic_name)

demo

sarima_demo

import pymysql                                   # 数据库
# 导入mylib
import sys
sys.path.append('/var/www/html/NewTest/InternShipProject/my_pylib')
from my_time_series_algorithm import *# read_sql(sql, con, index_col=None, coerce_float=True, params=None, parse_dates=None, columns=None, chunksize=None)
conn = pymysql.connect(	host = 'localhost',	user = 'root',	passwd = '123456',	db = 'prod_179',	port=3306,	charset = 'utf8'	
)	
df = pd.read_sql('select * from 北京市',conn)tsplot(df.rtt, lags=60)

exp_smooth_demo

import pymysql                                   # 数据库
# 导入mylib
import sys
sys.path.append('/var/www/html/NewTest/InternShipProject/my_pylib')
from my_time_series_algorithm import *# read_sql(sql, con, index_col=None, coerce_float=True, params=None, parse_dates=None, columns=None, chunksize=None)
conn = pymysql.connect(	host = 'localhost',	user = 'root',	passwd = '123456',	db = 'prod_179',	port=3306,	charset = 'utf8'	
)	
df = pd.read_sql('select * from all_nums where id between 864 and 1008',conn)# 双指数
# 绘制双指数平滑曲线 
def plotDoubleExponentialSmoothingXXX(series, alpha, beta, pic_name="plotExponentialSmoothing"):"""Plots double exponential smoothing with different alphas and betasseries - dataset with timestampsalphas - list of floats, smoothing parameters for levelbetas - list of floats, smoothing parameters for trend"""with plt.style.context('seaborn-white'):    plt.figure(figsize=(20, 8))res_line = double_exponential_smoothing(series, alpha, beta)print(res_line[-1])plt.plot(res_line, label="Alpha {}, beta {}".format(alpha, beta))plt.plot(series.values, label = "Actual")plt.legend(loc="best")plt.axis('tight')plt.title("Double Exponential Smoothing")plt.savefig('/var/www/html/NewTest/pics/%s.png' % pic_name)plt.grid(True)# plotDoubleExponentialSmoothingXXX(df.user_nums,0.9, 0.49, pic_name="双指数平滑效果")
plotDoubleExponentialSmoothing(df.user_nums, [0.78], [0.125, 0.1], pic_name="双指数平滑效果")
conn.close()
# # 单指数
# plotExponentialSmoothing(df.rtt, [0.3, 0.05])

linear_reg_demo

import pymysql                                   # 数据库
# 导入mylib
import sys
sys.path.append('/var/www/html/NewTest/InternShipProject/my_pylib')
from my_machine_learning_algorithm import *# read_sql(sql, con, index_col=None, coerce_float=True, params=None, parse_dates=None, columns=None, chunksize=None)
conn = pymysql.connect(	host = 'localhost',	user = 'root',	passwd = '123456',	db = 'prod_179',	port=3306,	charset = 'utf8'	
)	
df = pd.read_sql('select * from 北京市',conn)	# Creating a copy of the initial datagrame to make various transformations 
data = pd.DataFrame(df.rtt.copy())
data.columns = ["y"]# Adding the lag of the target variable from 6 steps back up to 24
for i in range(6, 25):data["lag_{}".format(i)] = data.y.shift(i)# for time-series cross-validation set 5 folds 
tscv = TimeSeriesSplit(n_splits=5)y = data.dropna().y
x = data.dropna().drop(['y'], axis=1)# reserve 30% of data for testing
x_train, x_test, y_train, y_test = timeseries_train_test_split(x, y, test_size=0.3)# # machine learning in two lines
lr = LinearRegression()
lr.fit(x_train, y_train.values.reshape(-1,1))
# # print(x_train.shape)
# # print(y_train.shape)
# # (527, 19)
# # (527,)
plotModelResults(lr, x_train, x_test, y_test, y_train, tscv, plot_intervals=True)
plotCoefficients(lr, x_train)

xgb_demo

import pymysql                                   # 数据库
# 导入mylib
import sys
sys.path.append('/var/www/html/NewTest/InternShipProject/my_pylib')
from my_machine_learning_algorithm import *# read_sql(sql, con, index_col=None, coerce_float=True, params=None, parse_dates=None, columns=None, chunksize=None)
conn = pymysql.connect(	host = 'localhost',	user = 'root',	passwd = '123456',	db = 'prod_179',	port=3306,	charset = 'utf8'	
)	
df = pd.read_sql('select * from all_nums',conn)# Creating a copy of the initial datagrame to make various transformations 
data = pd.DataFrame(df.flow_up.copy())
data.columns = ["y"]# Adding the lag of the target variable from 6 steps back up to 24
# for i in range(6, 25):
#     data["lag_{}".format(i)] = data.y.shift(i)# for time-series cross-validation set 5 folds 
tscv = TimeSeriesSplit(n_splits=5)y = data.dropna().y
x = data.dropna().drop(['y'], axis=1)# reserve 30% of data for testing
x_train, x_test, y_train, y_test = timeseries_train_test_split(x, y, test_size=0.3)X_train_scaled = scaler.fit_transform(x_train)
X_test_scaled = scaler.transform(x_test)xgb = XGBRegressor()
xgb.fit(X_train_scaled, y_train)plotModelResults(xgb, X_train=X_train_scaled, X_test=X_test_scaled, y_test=y_test,y_train=y_train,tscv=tscv,plot_intervals=True, plot_anomalies=True)