最后一次NOIP模拟了·····
题目1:回文数字
Tom 最近在研究回文数字。
假设 s[i] 是长度为 i 的回文数个数(不含前导0),则对于给定的正整数 n 有:
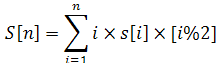
以上等式中最后面的括号是布尔表达式,Tom 想知道S[n] mod 233333 的值是多少。
输入格式
第一行一个正整数 T 。
接下来输出共 T 行,每行一个正整数 n 。
输出格式
输出共 T 行,每行一个整数,表示 S[n] mod 233333 。
样例数据 1
输入 [复制]
1
2
输出
9
备注
【数据规模与约定】
对于 30% 的数据:n≤5。
对于另 20% 的数据:∑n≤10^7。
对于另 20% 的数据:T=1。
对于 100% 的数据:T≤5*10^5;n≤10^9。
根据题意可以推出来就是一个差比数列·····用快速幂和逆元(中间有除法)求解即可
然而考试的时候作死cout<<endl直接超时····下次输出换行一定要用cout<<"\n“·····
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<ctime> #include<cctype> #include<cstring> #include<string> #include<algorithm> using namespace std; const long long mod=233333; const long long niyuan=25926; long long a,T; inline long long R(){char c;long long f=0;for(c=getchar();c<'0'||c>'9';c=getchar());for(;c<='9'&&c>='0';c=getchar()) f=(f<<3)+(f<<1)+c-'0';return f; } inline long long ksm(long long a,long long b){long long ans=1;a%=mod;while(b){if(b&1) ans=ans*a%mod;b/=2;a=a*a%mod;}return ans; } int main(){//freopen("bug.in","r",stdin);//freopen("bug.out","w",stdout);T=R();while(T--){a=R();if(a==1||a==2) cout<<"9"<<endl;else{a=(a-1)/2; long long b=ksm(10,a+1);long long c=b;b=b*((2*a%mod+1)%mod)%mod;c=(c-10)*niyuan%mod*2%mod;b=((b-1-c)%mod+mod)%mod;cout<<b<<"\n";}}return 0; }
题目2:路径统计
一个 n 个点 m 条边的无重边无自环的无向图,点有点权,边有边权,定义一条路径的权值为路径经过的点权的最大值乘边权最大值。
求任意两点间的权值最小的路径的权值。
输入格式
第一行两个整数 n ,m ,分别表示无向图的点数和边数。
第二行 n 个正整数,第 i 个正整数表示点i的点权。
接下来 m 行每行三个正整数 ui,vi,wi ,分别描述一条边的两个端点和边权。
输出格式
输出 n 行,每行 n 个整数。
第 i 行第 j 个整数表示从 i 到 j 的路径的最小权值;如果从 i 不能到达 j ,则该值为 -1 。特别地,当 i=j 时输出 0 。
样例数据 1
输入 [复制]
3 3
2 3 3
1 2 2
2 3 3
1 3 1
输出
0 6 3
6 0 6
3 6 0
备注
【样例输入输出2】
见选手目录下path.in/path.ans。
【数据范围与约定】
对于 20% 的数据:n≤5;m≤8。
对于 50% 的数据:n≤50。
对于 100% 的数据:n≤500;m≤n*(n-1)/2,边权和点权不超过10^9 。
考虑直接用floyd的话会出现错误···比如说我们用k1更新f[i][j]后,下次用k2更新f[i][j]时可能会出错····
方法是我们将每个点的点权从小到大排序··在枚举最外层的中转点时我们按升序枚举···这样就能保证正确性,具体怎么证明这里就不多写了···
注意能开int的地方就开int··不然要超时
#include<iostream> #include<cstdio> #include<cstdlib> #include<string> #include<cstring> #include<algorithm> #include<cmath> #include<ctime> #include<cctype> using namespace std; const int N=505; struct node{int val,id; }p[N]; int n,m,mp[N][N],val[N],me[N][N]; long long dis[N][N]; bool Visit[N],jud[N][N]; inline int R(){char c;int f=0;for(c=getchar();c<'0'||c>'9';c=getchar());for(;c<='9'&&c>='0';c=getchar()) f=(f<<3)+(f<<1)+c-'0';return f; } inline long long Rl(){char c;long long f=0;for(c=getchar();c<'0'||c>'9';c=getchar());for(;c<='9'&&c>='0';c=getchar()) f=(f<<3)+(f<<1)+c-'0';return f; } int buf[1024]; inline void write(long long x){if(!x){putchar('0');return ;}if(x<0){putchar('-');x=-x;}while(x){buf[++buf[0]]=x%10,x/=10;}while(buf[0]) putchar(buf[buf[0]--]+48);return ; } inline bool cmp(const node &a,const node &b){return a.val<b.val; } int main(){//freopen("path.in","r",stdin);///freopen("path1.out","w",stdout);n=R();m=R();int a,b;long long c;memset(jud,false,sizeof(jud));for(int i=1;i<=n;i++)for(int j=1;j<=n;j++) mp[i][j]=me[i][j]=1e+9,dis[i][j]=2e+18;for(int i=1;i<=n;i++) val[i]=R(),p[i].val=val[i],p[i].id=i;sort(p+1,p+1+n,cmp);for(int i=1;i<=m;i++){a=R(),b=R(),c=R();me[a][b]=me[b][a]=c;mp[a][b]=mp[b][a]=max(val[a],val[b]);jud[a][b]=jud[b][a]=true;dis[a][b]=dis[b][a]=(long long)mp[b][a]*me[b][a];}for(int K=1;K<=n;K++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){int k=p[K].id;if(!jud[i][k]||!jud[k][j]||i==j) continue;int maxp=max(mp[i][k],mp[k][j]); int maxe=max(me[i][k],me[k][j]);if((long long)maxp*maxe<dis[i][j]){dis[i][j]=(long long)maxp*maxe;mp[i][j]=maxp;me[i][j]=maxe;jud[i][j]=true;}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i==j) write(0),putchar(' ');else if(jud[i][j]) write(dis[i][j]),putchar(' ');else write(-1),putchar(' ');}putchar('\n');}return 0;}
题目3:字符串
给定两个字符串 s1 和 s2 ,两个字符串都由 26 个小写字母中的部分字母构成。现在需要统计 s2 在 s1 中出现了的次数。
对于 s1 中的每个位置 i ,设 strlen(s2)=m ,若:
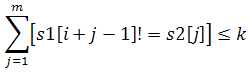
(最外层中括号为布尔表达式)
则认为 s2 在 s1 的 i 处出现了一次,现在想知道,s2 在 s1 中一共出现了多少次?
输入格式
第一行为一个字符串 s1 ;
第二行为一个字符串 s2 ;
第三行为一个整数 k 。
输出格式
输出一行一个整数,表示 s2 在 s1 中出现的次数。
样例数据 1
输入 [复制]
ababbab
aba
1
输出
3
备注
【数据范围与约定】
前 10% 的数据:n>m。
前 30% 的数据:n,m≤1000。
对于另 40% 的数据:k≤20。
对于 100% 的数据:n≤200000;m≤100000;k≤100。
由于正解要用到后缀数组不属于NOIP范围··所以这里我就先挖个坑吧··只讲讲70分
暴力肯定是枚举每一个起始位置暴力匹配···70分算法就是它的优化··每次匹配的时候我们用hash+二分来匹配即可
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<ctime> #include<cctype> #include<string> #include<cstring> #include<algorithm> using namespace std; const int N=2e5+5; const int base=61; int n,m,ans=0,k; unsigned long long bt[N],hash1[N],hash2[N]; char s1[N],s2[N]; inline void pre(){bt[0]=1;for(int i=1;i<=n;i++) bt[i]=bt[i-1]*base;for(int i=n;i>=1;i--) hash1[i]=hash1[i+1]*base+s1[i]-'a';for(int i=m;i>=1;i--) hash2[i]=hash2[i+1]*base+s2[i]-'a'; } inline int getans(int st){int cnt=0,po=1;while(cnt<=k&&po<=m){int le=0,ri=m-po;while(le<=ri){int mid=(ri+le)/2;if((hash2[po]-hash2[po+mid+1]*bt[mid+1])==(hash1[st+po-1]-hash1[st+po+mid]*bt[mid+1])) le=mid+1;else ri=mid-1;}if(po+ri!=m) cnt++;po=po+ri+2;}if(cnt<=k) return 1;else return 0; } int main(){//freopen("a.in","r",stdin);scanf("%s%s",s1+1,s2+1);scanf("%d",&k);n=strlen(s1+1);m=strlen(s2+1);pre();for(int i=1;i<=n-m+1;i++) ans+=getans(i);cout<<ans<<"\n";return 0; }





)


![[ JavaScript ] JavaScript 实现继承.](http://pic.xiahunao.cn/[ JavaScript ] JavaScript 实现继承.)










