现实生活中，我们经常提到距离这个词，本文谈的相似度就是基于距离定义的，当两个向量之间的距离特别小时，就说这俩个向量相似度高，反之相似度不高。所以，衡量相似度的指标就是距离度量。
经常使用的相似度计算公式有：欧几里得相似度、余弦相似度、皮尔逊相似度、曼哈顿相似度。
（1）欧几里得相似度：
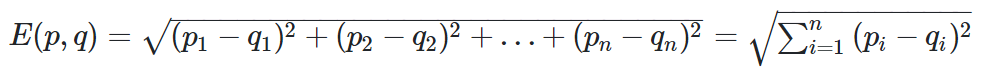
import numpy as np
def eculidDisSim(x,y):'''欧几里得相似度'''return np.sqrt(sum(pow(a-b,2) for a,b in zip(x,y)))
if __name__=='__main__':a=np.array([1,2,3])b=np.array([6,5,4])sim=eculidDisSim(a,b)（2）余弦相似度：
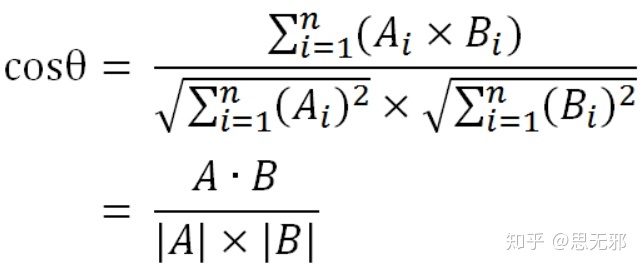
import numpy as np
def cosSim(x,y):'''余弦相似度'''tmp=np.sum(x*y)non=np.linalg.norm(x)*np.linalg.norm(y)return np.round(tmp/float(non),9)if __name__=='__main__':a=np.array([1,2,3])b=np.array([6,5,4])sim=cosSim(a,b)（3）皮尔逊（pearsonr）相似度：
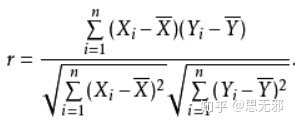
from scipy.stats import pearsonr
import numpy as np
def pearsonrSim(x,y):'''皮尔森相似度'''return pearsonr(x,y)[0]if __name__=='__main__':a=np.array([1,2,3])b=np.array([6,5,4])sim=pearsonrSim(a,b)（4）曼哈顿相似度：
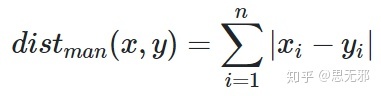
import numpy as np
def manhattanDisSim(x,y):'''曼哈顿相似度'''return sum(abs(a-b) for a,b in zip(x,y))if __name__=='__main__':a=np.array([1,2,3])b=np.array([6,5,4])sim=manhattanDisSim(a,b)
