树-二叉树、满二叉树和完全二叉树

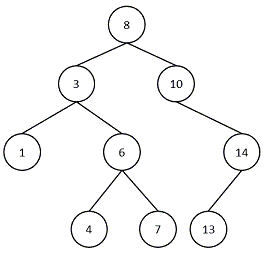
二叉树的定义：

（1）当n=0时，为空树；

（2）当n>0时，是由一个根结点和称为根结点的左、右子树构成，并且两颗子树互不相交。

满二叉树：

对于一棵二叉树，如果每一个非叶子节点都存在左右子树，并且所有的叶子结点都在同一层中。

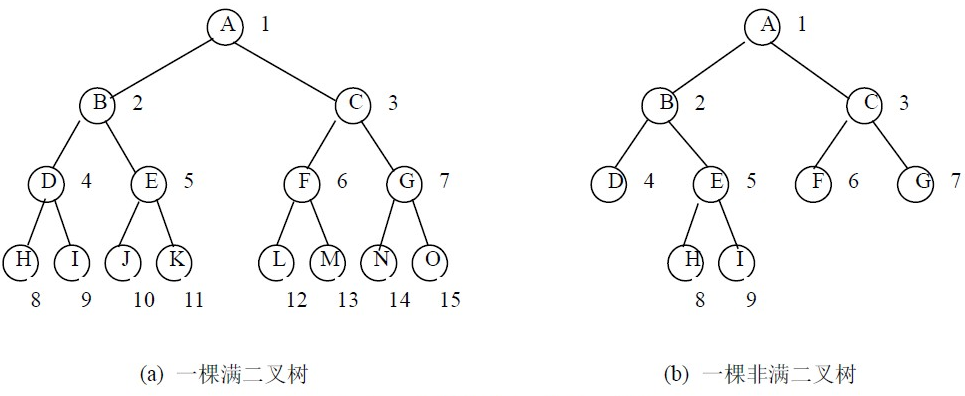
完全二叉树：

如果一棵具有n个结点的深度为k的二叉树，它的每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应，这棵二叉树称为完全二叉树。满二叉树必定是完全二叉树。

 

二叉树性质：

1、一棵非空二叉树的第i层上最多有 2ⁱ-1 个结点（i ≥ 1）。

2、一棵深度为k的二叉树中，最多有 2^k-1个结点。

3、对于一棵非空的二叉树，如果叶子结点数为n₀，度数为2的结点数为n₂，则有: n₀ = n₂+1

4、具有n个结点的完全二叉树的深度k为 [log₂ⁿ] + 1

二叉树的遍历：

1、前序遍历：先遍历根节点，再遍历左子树 ，再遍历右子树 

2、中序遍历：先遍历左子树，再遍历根节点，最后遍历右子树 

3、后续遍历：先遍历左子树，再遍历右子树，最后遍历根节点